Задача о наименьшем круге

Задача о наименьшей окружности ( также известная как задача о минимальной покрывающей окружности , задача о ограничивающей окружности , задача о наименьшей ограничивающей окружности , задача о наименьшей охватывающей окружности ) — это задача вычислительной геометрии по вычислению наименьшей окружности , содержащей все заданные множества точек на евклидовой плоскости . Соответствующая задача в n -мерном пространстве , задача о наименьшей ограничивающей сфере , заключается в вычислении наименьшей n -сферы , содержащей все заданные множества точек. [1] Задача о наименьшей окружности была первоначально предложена английским математиком Джеймсом Джозефом Сильвестром в 1857 году. [2]
Задача о наименьшем круге на плоскости является примером задачи о размещении объекта ( задача с одним центром ), в которой местоположение нового объекта должно быть выбрано таким образом, чтобы обеспечить обслуживание определенного количества клиентов, минимизируя наибольшее расстояние, которое должен преодолеть любой клиент, чтобы добраться до нового объекта. [3] Как задача о наименьшем круге на плоскости, так и задача о наименьшей ограничивающей сфере в любом многомерном пространстве ограниченной размерности разрешимы за наихудшее линейное время .
Характеристика
Большинство геометрических подходов к этой задаче ищут точки, лежащие на границе минимального круга, и основаны на следующих простых фактах:
- Минимальный покрывающий круг единственен.
- Минимальная охватывающая окружность множества S может быть определена не более чем тремя точками в S , лежащими на границе окружности. Если она определяется только двумя точками, то отрезок прямой, соединяющий эти две точки, должен быть диаметром минимальной окружности. Если она определяется тремя точками, то треугольник, состоящий из этих трех точек, не является тупоугольным .
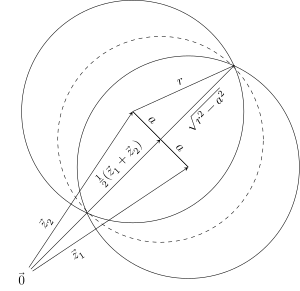
Доказательство того, что минимальный покрывающий диск уникален |
|---|
Пусть P — любой набор точек на плоскости, и предположим, что есть два наименьших охватывающих диска P с центрами в и . Пусть — их общий радиус , а — расстояние между их центрами. Поскольку P — подмножество обоих дисков, оно является подмножеством их пересечения . Однако их пересечение содержится внутри диска с центром и радиусом , как показано на следующем изображении: Поскольку r минимально, то должно быть , то есть , поэтому диски идентичны. [4] |
Решения с линейным временем
Как показал Нимрод Мегиддо , [5] минимальная охватывающая окружность может быть найдена за линейное время, и та же самая линейная временная граница применима также к наименьшей охватывающей сфере в евклидовых пространствах любой постоянной размерности. Его статья также дает краткий обзор более ранних и алгоритмов; [6] при этом Мегиддо продемонстрировал, что гипотеза Шамоса и Хоя — о том, что решение задачи наименьшей окружности вычислимо в лучшем случае за — была ложной. [7]
Эмо Вельцль [8] предложил простой рандомизированный алгоритм для задачи минимального покрывающего круга, который выполняется за ожидаемое время , основанный на алгоритме линейного программирования Раймунда Зайделя .
Впоследствии задача наименьшего круга была включена в общий класс задач типа LP , которые могут быть решены такими алгоритмами, как алгоритм Вельцля, основанный на линейном программировании. Вследствие принадлежности к этому классу было показано, что зависимость от размерности постоянного множителя в ограничении по времени, которая была факториальной для метода Зейделя, может быть сведена к субэкспоненциальной . [6] Алгоритм минидиска Вельцля был расширен для обработки расхождений Брегмана [9] , которые включают квадрат евклидова расстояния.
Алгоритм Мегиддо
Алгоритм Мегиддо [10] основан на технике, называемой обрезкой и поиском, уменьшающей размер проблемы путем удаления ненужных точек. Это приводит к повторению, дающему .
Алгоритм довольно сложен, и это отражается в его большой мультипликативной константе. Редукция должна решить дважды аналогичную задачу, где центр искомого охватывающего круга ограничен лежать на заданной прямой . Решение подзадачи является либо решением безусловной задачи, либо используется для определения полуплоскости, где находится центр безусловного решения.
Точки , которые следует отбросить, находятся следующим образом: Точки P i объединяются в пары, которые определяют прямые p j как их биссектрисы . Находится медианное среднее p m биссектрис в порядке их направлений (ориентированных на одну и ту же полуплоскость, определяемую биссектрисой p 1 ), и составляются пары биссектрис таким образом, что в каждой паре одна биссектриса имеет направление не более p m , а другая не менее p m (направление p 1 можно рассматривать как − или + в зависимости от наших потребностей.) Пусть Q k будет пересечением биссектрис в k -й паре.
Прямая q в направлении p 1 помещается так, чтобы проходить через пересечение Q x таким образом, чтобы в каждой полуплоскости, определяемой прямой, имелись пересечения (срединное положение). Ограниченная версия объемлющей задачи выполняется на прямой q', которая определяет полуплоскость, в которой расположен центр. Прямая q ′ в направлении p m помещается так, чтобы проходить через пересечение Q x' таким образом, чтобы в каждой половине полуплоскости, не содержащей решения, имелись пересечения. Ограниченная версия объемлющей задачи выполняется на прямой q ′, которая вместе с q определяет квадрант, в котором расположен центр. Мы рассматриваем точки Q k в квадранте, не содержащемся в полуплоскости, содержащей решение. Одна из биссектрис пары, определяющей Q k, имеет направление, гарантирующее, какая из точек P i , определяющих биссектрису, находится ближе к каждой точке в квадранте, содержащем центр объемлющей окружности. Эту точку можно отбросить.
Ограниченная версия алгоритма также решается методом отсечения и поиска, но с уменьшением размера задачи за счет удаления точек, приводящих к повторению.
давая .
Точки , которые нужно отбросить, находятся следующим образом: Точки P i объединяются в пары. Для каждой пары находится пересечение Q j ее биссектрисы с ограничивающей прямой q (Если этого пересечения не существует, мы могли бы немедленно удалить одну точку из пары). Находится медиана M точек Q j на прямой q и за время O ( n ) определяется, какая полупрямая q, начинающаяся в M, содержит решение ограниченной задачи. Мы рассматриваем точки Q j из другой половины. Мы знаем, какая из точек P i, определяющих Q j, находится ближе к каждой точке полупрямой, содержащей центр охватывающей окружности решения ограниченной задачи. Эту точку можно отбросить.
Полуплоскость, в которой лежит решение без ограничений, может быть определена точками P i на границе решения в виде ограниченного круга. (Достаточно первой и последней точки на круге в каждой полуплоскости. Если центр принадлежит их выпуклой оболочке , то это решение без ограничений, в противном случае направление к ближайшему краю определяет полуплоскость решения без ограничений.)
Алгоритм Вельцля
Алгоритм рекурсивный .
Начальный ввод — это набор точек P. Алгоритм выбирает одну точку p случайным образом и равномерно из P и рекурсивно находит минимальный круг, содержащий P – { p }, т. е. все остальные точки в P , кроме p . Если возвращаемый круг также охватывает p , то это минимальный круг для всего P и он возвращается.
В противном случае точка p должна лежать на границе результирующего круга. Он рекурсивен, но с набором R точек, которые, как известно, находятся на границе, в качестве дополнительного параметра.
Рекурсия заканчивается, когда P пусто , и решение может быть найдено из точек в R : для 0 или 1 точки решение тривиально, для 2 точек минимальный круг имеет центр в средней точке между двумя точками, а для 3 точек круг является описанной окружностью треугольника , описываемого точками. (В трех измерениях 4 точки требуют вычисления описанной сферы тетраэдра .)
Рекурсия также может завершиться, когда R имеет размер 3 (в 2D или 4 в 3D), поскольку оставшиеся точки в P должны лежать внутри окружности, описанной R.
Алгоритм welzl [8] : входные данные: конечные множества P и R точек на плоскости | R | ≤ 3. выходные данные: минимальный диск, охватывающий P с R на границе. если P пусто или | R | = 3 , то вернуть trivial( R ) выбрать p из P ( случайным образом и равномерно ) D := welzl( P − { p }, R ) если p находится в D, то вернуть D вернуть welzl( P − { p }, R ∪ { p })
В статье Вельцля утверждается, что достаточно случайным образом переставлять входные данные в начале, а не выполнять независимый случайный выбор p в каждой рекурсии.
В нем также говорится, что производительность повышается за счет динамического переупорядочивания точек, так что те, которые оказываются за пределами круга, впоследствии рассматриваются раньше, но это требует изменения структуры алгоритма для сохранения P как «глобального».
Другие алгоритмы
До результата Мегиддо, показывающего, что задача наименьшего круга может быть решена за линейное время, в литературе появилось несколько алгоритмов более высокой сложности. Наивный алгоритм решает задачу за время O( n 4 ) путем проверки кругов, определяемых всеми парами и тройками точек.
- Алгоритм Кристала и Пирса применяет стратегию локальной оптимизации , которая сохраняет две точки на границе охватывающего круга и многократно сжимает круг, заменяя пару граничных точек, пока не будет найден оптимальный круг. Чакраборти и Чаудхури [11] предлагают метод линейного времени для выбора подходящего начального круга и пары граничных точек на этом круге. Каждый шаг алгоритма включает в качестве одной из двух граничных точек новую вершину выпуклой оболочки , поэтому, если оболочка имеет h вершин, этот метод может быть реализован для выполнения за время O( nh ).
- Элзинга и Хирн [12] описали алгоритм, который поддерживает покрывающую окружность для подмножества точек. На каждом шаге точка, не покрытая текущей сферой, используется для поиска большей сферы, которая покрывает новое подмножество точек, включая найденную точку. Хотя в худшем случае время выполнения составляет O( h 3 n ), авторы сообщают, что в их экспериментах он работал за линейное время. Сложность метода была проанализирована Дрезнером и Шелахом. [13] Коды на Фортране и С доступны в Hearn, Vijay & Nickel (1995). [14]
- Задача наименьшей сферы может быть сформулирована как квадратичная программа [1], определяемая системой линейных ограничений с выпуклой квадратичной целевой функцией. Следовательно, любой алгоритм допустимого направления может дать решение задачи. [15] Хирн и Виджай [16] доказали, что подход допустимого направления, выбранный Якобсеном, эквивалентен алгоритму Кристала–Пирса.
- Двойственный к этой квадратичной программе алгоритм также может быть сформулирован явно [17] ; алгоритм Лоусона [18] может быть описан таким образом как первичный двойственный алгоритм. [16]
- Шамос и Хоуи [7] предложили алгоритм времени O( n log n ) для этой задачи, основанный на наблюдении, что центр наименьшего охватывающего круга должен быть вершиной самой дальней точки диаграммы Вороного входного набора точек.
Взвешенные варианты задачи
Взвешенная версия задачи минимального покрывающего круга принимает в качестве входных данных набор точек в евклидовом пространстве, каждая из которых имеет вес; цель состоит в том, чтобы найти одну точку, которая минимизирует максимальное взвешенное расстояние (т. е. расстояние, умноженное на соответствующий вес) до любой точки. Исходная (невзвешенная) задача минимального покрывающего круга соответствует случаю, когда все веса равны 1. Как и в случае с невзвешенной задачей, взвешенная задача может быть решена за линейное время в любом пространстве ограниченной размерности, используя подходы, тесно связанные с алгоритмами линейного программирования ограниченной размерности, хотя в литературе снова часто встречаются более медленные алгоритмы. [16] [19] [20]
Наименьшие охватывающие шары в неевклидовой геометрии
Наименьший охватывающий шар конечного множества точек изучался в римановой геометрии, включая многообразия Картана-Адамара. [21]
Смотрите также
Ссылки
- ^ ab Elzinga, J.; Hearn, DW (1972), "Проблема минимальной сферы покрытия", Management Science , 19 : 96–104, doi :10.1287/mnsc.19.1.96
- ^ Сильвестр, Дж. Дж. (1857), «Вопрос в геометрии положения», Quarterly Journal of Mathematics , 1 : 79.
- ^ Фрэнсис, Р. Л.; Макгиннис, Л. Ф.; Уайт, Дж. А. (1992), Планировка и расположение объекта: аналитический подход (2-е изд.), Энглвуд Клиффс, Нью-Джерси: Prentice–Hall, Inc..
- ^ Вельцль 1991, стр. 2.
- ^ Мегиддо, Нимрод (1983), «Линейные алгоритмы для линейного программирования в R 3 и связанные с ними проблемы», SIAM Journal on Computing , 12 (4): 759–776, doi :10.1137/0212052, MR 0721011, S2CID 14467740.
- ^ ab Matoušek, Jiří ; Sharir, Micha ; Welzl, Emo (1996), "Субэкспоненциальная граница для линейного программирования" (PDF) , Algorithmica , 16 (4–5): 498–516, CiteSeerX 10.1.1.46.5644 , doi :10.1007/BF01940877, S2CID 877032 .
- ^ ab Shamos, MI ; Hoey, D. (1975), «Проблемы с ближайшими точками», Труды 16-го ежегодного симпозиума IEEE по основам компьютерной науки , стр. 151–162, doi : 10.1109/SFCS.1975.8, S2CID 40615455
- ^ ab Welzl, Emo (1991), "Наименьшие охватывающие диски (шары и эллипсоиды)", в Maurer, H. (ред.), Новые результаты и новые тенденции в компьютерной науке , Lecture Notes in Computer Science, т. 555, Springer-Verlag, стр. 359–370, CiteSeerX 10.1.1.46.1450 , doi :10.1007/BFb0038202, ISBN 978-3-540-54869-0.
- ^ Нильсен, Франк; Нок, Ричард (2008), «О наименьшем содержащемся информационном диске», Information Processing Letters , 105 (3): 93–97, doi :10.1016/j.ipl.2007.08.007
- ^ Мегиддо, Нимрод (1983), «Линейные алгоритмы для линейного программирования в R 3 и связанные с ними проблемы», SIAM Journal on Computing , 12 (4): 759–776, doi :10.1137/0212052, MR 0721011, S2CID 14467740.
- ^ Чакраборти, РК; Чаудхури, П.К. (1981), «Заметка о геометрических решениях для некоторых минимаксных задач размещения», Transportation Science , 15 (2): 164–166, doi : 10.1287/trsc.15.2.164.
- ^ Элзинга, Дж.; Хирн, Д.У. (1972), «Геометрические решения для некоторых минимаксных задач размещения», Transportation Science , 6 (4): 379–394, doi :10.1287/trsc.6.4.379.
- ^ Дрезнер, Цви; Шелах, Сахарон (1987), «О сложности алгоритма Элзинги–Хирна для задачи с одним центром», Математика исследования операций , 12 (2): 255–261, doi :10.1287/moor.12.2.255, JSTOR 3689688.
- ^ Hearn, DW; Vijay, J.; Nickel, S. (1995), «Коды геометрических алгоритмов для задачи (взвешенного) минимального круга», European Journal of Operational Research , 80 : 236–237, doi :10.1016/0377-2217(95)90075-6.
- ^ Якобсен, SK (1981), «Алгоритм для минимаксной задачи Вебера», Европейский журнал операционных исследований , 6 (2): 144–148, doi :10.1016/0377-2217(81)90200-9.
- ^ abc Hearn, DW; Vijay, J. (1982), "Эффективные алгоритмы для задачи (взвешенного) минимального круга", Operations Research , 30 (4): 777–795, doi :10.1287/opre.30.4.777.
- ^ Elzinga, J.; Hearn, DW; Randolph, WD (1976), «Минимаксное многообъектное расположение с евклидовыми расстояниями», Transportation Science , 10 (4): 321–336, doi :10.1287/trsc.10.4.321.
- ^ Лоусон, CL (1965), «Наименьший покрывающий конус или сфера», SIAM Review , 7 (3): 415–417, doi :10.1137/1007084.
- ^ Мегиддо, Н. (1983), «Взвешенная евклидова задача с одним центром», Математика исследования операций , 8 (4): 498–504, doi :10.1287/moor.8.4.498.
- ^ Мегиддо, Н.; Земель, Э. (1986), « О ( n log n ) рандомизирующий алгоритм для взвешенной евклидовой проблемы с 1 центром», Журнал алгоритмов , 7 (3): 358–368, doi :10.1016/0196-6774(86)90027-1.
- ^ Арнодон, Марк; Нильсен, Франк (2013), «Об аппроксимации риманова 1-центра», Computational Geometry , 46 (1): 93–104, arXiv : 1101.4718 , doi : 10.1016/j.comgeo.2012.04.007
Внешние ссылки
- Самый маленький код охватывающего шара Бернда Гертнера
- CGAL — пакет Min_sphere_of_spheres библиотеки алгоритмов вычислительной геометрии (CGAL)
- Miniball — реализация алгоритма с открытым исходным кодом для задачи о наименьшем объемлющем шаре для низких и умеренно высоких размерностей.