Отбор проб срезов

Выборка среза — это тип алгоритма Монте-Карло цепи Маркова для выборки псевдослучайных чисел , т. е. для получения случайных выборок из статистического распределения. Метод основан на наблюдении, что для выборки случайной величины можно сделать равномерную выборку из области под графиком ее функции плотности. ^{[1] [2] [3]}

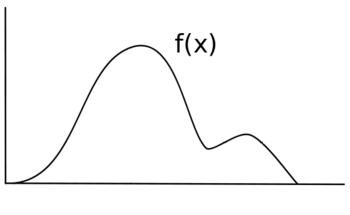
Предположим, вы хотите сделать выборку некоторой случайной величины X с распределением f ( x ). Предположим, что ниже представлен график f ( x ). Высота f ( x ) соответствует вероятности в этой точке.

Если бы вы равномерно сэмплировали X , каждое значение имело бы одинаковую вероятность быть сэмплированным, и ваше распределение имело бы вид f ( x ) = y для некоторого значения y вместо некоторой неравномерной функции f ( x ). Вместо исходной черной линии ваше новое распределение было бы больше похоже на синюю линию.

Для того чтобы сделать выборку X таким образом, чтобы сохранить распределение f ( x ), необходимо использовать определенную технику выборки, которая учитывает различные вероятности для каждого диапазона f ( x ).

В простейшей форме срезовая выборка равномерно отбирает данные из-под кривой f ( x ) без необходимости отбрасывать какие-либо точки, как показано ниже:

1. Выберите начальное значение x _{0 ,} для которого f ( x ₀ ) > 0.
2. Выбрать значение y равномерно между 0 и f ( x ₀ ).
3. Нарисуйте горизонтальную линию поперек кривой в этой точке Y.
4. Выберите точку ( x , y ) из сегментов линии внутри кривой.
5. Повторите действия с шага 2, используя новое значение x .

Мотивация здесь в том, что один из способов равномерной выборки точки из произвольной кривой — сначала нарисовать тонкие горизонтальные срезы одинаковой высоты по всей кривой. Затем мы можем сделать выборку точки внутри кривой, случайным образом выбрав срез, который попадает на кривую или ниже ее в x-позиции из предыдущей итерации, а затем случайным образом выбрав x-позицию где-нибудь вдоль среза. Используя x-позицию из предыдущей итерации алгоритма, в конечном счете мы выбираем срезы с вероятностями, пропорциональными длинам их сегментов внутри кривой. Самая сложная часть этого алгоритма — нахождение границ горизонтального среза, что включает в себя инвертирование функции, описывающей распределение, из которого производится выборка. Это особенно проблематично для многомодальных распределений, где срез может состоять из нескольких прерывистых частей. Часто можно использовать форму выборки с отклонением, чтобы преодолеть это, когда мы делаем выборку из большего среза, который, как известно, включает желаемый рассматриваемый срез, а затем отбрасываем точки за пределами желаемого среза. Этот алгоритм можно использовать для выборки из области под любой кривой, независимо от того, интегрируется ли функция до 1. Фактически, масштабирование функции на константу не влияет на выборочные x-позиции. Это означает, что алгоритм можно использовать для выборки из распределения, функция плотности вероятности которого известна только с точностью до константы (т. е. нормирующая константа которого неизвестна), что является обычным явлением в вычислительной статистике .

Выборка среза получила свое название от первого шага: определения среза путем выборки из вспомогательной переменной . Эта переменная выбирается из , где либо является функцией плотности вероятности (PDF) X , либо по крайней мере пропорциональна ее PDF. Это определяет срез X , где . Другими словами, теперь мы смотрим на область X , где плотность вероятности по крайней мере . Затем следующее значение X выбирается равномерно из этого среза. Выбирается новое значение , затем X и так далее. Это можно визуализировать как альтернативную выборку y-позиции, а затем x-позиции точек под PDF, таким образом, X берутся из желаемого распределения. Значения не имеют особых последствий или интерпретаций за пределами их полезности для процедуры.${\displaystyle Y}$${\displaystyle [0,f(x)]}$${\displaystyle f(x)}$${\displaystyle f(x)\geq Y}$${\displaystyle Y}$${\displaystyle Y}$${\displaystyle Y}$

Если доступны как PDF, так и его обратная функция, а распределение унимодальное, то нахождение среза и выборка из него просты. Если нет, можно использовать процедуру выхода, чтобы найти область, конечные точки которой выходят за пределы среза. Затем можно извлечь образец из среза с помощью выборки с отклонением . Различные процедуры для этого подробно описаны Рэдфордом М. Нилом . ^[2]

Обратите внимание, что в отличие от многих доступных методов генерации случайных чисел из неравномерных распределений случайные переменные, сгенерированные непосредственно этим подходом, будут демонстрировать последовательную статистическую зависимость. Это связано с тем, что для построения следующей выборки мы определяем срез на основе значения f ( x ) для текущей выборки.

Slice sampling — это метод цепей Маркова, который служит той же цели, что и Gibbs sampling и Metropolis. В отличие от Metropolis, нет необходимости вручную настраивать функцию-кандидата или стандартное отклонение-кандидата.

Вспомним, что Metropolis чувствителен к размеру шага. Если размер шага слишком мал, случайное блуждание вызывает медленную декорреляцию. Если размер шага слишком велик, то возникает большая неэффективность из-за высокого уровня отбраковки.

В отличие от Metropolis, выборка среза автоматически подстраивает размер шага под локальную форму функции плотности. Реализация, возможно, проще и эффективнее, чем выборка Гиббса или простые обновления Metropolis.

Обратите внимание, что в отличие от многих доступных методов генерации случайных чисел из неравномерных распределений случайные переменные, генерируемые непосредственно этим подходом, будут демонстрировать последовательную статистическую зависимость. Другими словами, не все точки имеют одинаковую независимую вероятность выбора. Это связано с тем, что для построения следующей выборки мы определяем срез на основе значения f(x) для текущей выборки. Однако генерируемые выборки являются марковскими , и поэтому ожидается, что они будут сходиться к правильному распределению в долгосрочной перспективе.

Выборка срезов требует, чтобы распределение, подлежащее выборке, было оценочным. Один из способов смягчить это требование — заменить оценочное распределение, которое пропорционально истинному неоцениваемому распределению.

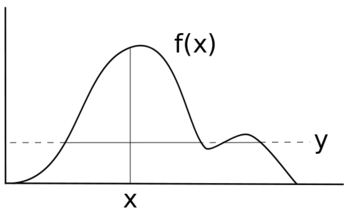
Для выборки случайной величины X с плотностью f ( x ) введем вспомогательную переменную Y и выполним итерацию следующим образом:

• При наличии выборки x мы выбираем y равномерно случайным образом из интервала [0, f ( x )];
• при заданном y мы выбираем x равномерно случайным образом из набора .${\displaystyle f^{-1}[y,+\infty )}$
• Выборка x получается путем игнорирования значений y .

Наша вспомогательная переменная Y представляет собой горизонтальный «срез» распределения. Оставшаяся часть каждой итерации посвящена выборке значения x из среза, которое является репрезентативным для плотности рассматриваемого региона.

На практике выборка из горизонтального среза мультимодального распределения затруднена. Существует напряжение между получением большой области выборки и, таким образом, возможностью больших перемещений в пространстве распределения, и получением более простой области выборки для повышения эффективности. Одним из вариантов упрощения этого процесса является региональное расширение и сужение.

• Во-первых, параметр ширины w используется для определения области, содержащей заданное значение 'x. Каждая конечная точка этой области проверяется на предмет того, лежит ли она за пределами заданного среза. Если нет, область расширяется в соответствующем направлении(ях) на w до тех пор, пока обе конечные точки не окажутся за пределами среза.
• Кандидатный образец выбирается равномерно из этой области. Если кандидатный образец лежит внутри среза, то он принимается как новый образец. Если он лежит вне среза, то точка-кандидат становится новой границей для области. Новый кандидатный образец выбирается равномерно. Процесс повторяется до тех пор, пока кандидатный образец не окажется внутри среза. (См. диаграмму для наглядного примера).

→

В сэмплере Гиббса необходимо эффективно извлекать данные из всех распределений с полным условием. Когда выборка из плотности с полным условием непроста, можно использовать одну итерацию выборки среза или алгоритм Метрополиса-Гастингса в Гиббсе для выборки из рассматриваемой переменной. Если плотность с полным условием является логарифмически вогнутой, более эффективной альтернативой является применение методов адаптивной выборки отклонения (ARS). ^{[4] [5]} Когда методы ARS не могут быть применены (поскольку плотность с полным условием не является логарифмически вогнутой), часто используются алгоритмы выборки Метрополиса с адаптивным отклонением . ^{[6] [7]}

Выборка среза с одной переменной может использоваться в многомерном случае путем выборки каждой переменной по очереди многократно, как в выборке Гиббса. Для этого требуется, чтобы мы могли вычислить для каждого компонента функцию, пропорциональную .${\displaystyle x_{i}}$${\displaystyle p(x_{i}|x_{0}...x_{n})}$

Чтобы предотвратить случайное блуждание, можно использовать методы сверхрелаксации для обновления каждой переменной по очереди. ^{[ требуется ссылка ]} Сверхрелаксация выбирает новое значение на противоположной стороне моды от текущего значения, в отличие от выбора нового независимого значения из распределения, как это делается в Гиббсе.

Этот метод адаптирует одномерный алгоритм к многомерному случаю, заменяя гиперпрямоугольником одномерную область w, используемую в оригинале. Гиперпрямоугольник H инициализируется в случайном положении над срезом. Затем H сжимается, поскольку точки из него отбрасываются.

Рефлективная срезовая выборка — это метод подавления случайного блуждания, при котором последовательные кандидатные выборки распределения f ( x ) удерживаются в пределах среза путем «отражения» направления выборки внутрь по направлению к срезу после достижения границы.

В этом графическом представлении отражательной выборки форма указывает границы среза выборки. Точки указывают начальную и конечную точки выборочного обхода. Когда выборки достигают границ среза, направление выборки «отражается» обратно в срез.

Рассмотрим пример с одной переменной. Предположим, что наше истинное распределение является нормальным со средним значением 0 и стандартным отклонением 3, . Итак: . Пик распределения, очевидно, находится в , в точке .${\displaystyle g(x)\sim N(0,3^{2})}$${\displaystyle f(x)={\frac {1}{\sqrt {2\pi \cdot 3^{2}}}}\ e^{-{\frac {(x-0)^{2}}{2\cdot 3^{2}}}}}$${\displaystyle x=0}$${\displaystyle f(x)\approx 0.1330}$

1. Сначала мы выбираем равномерное случайное значение y из диапазона f ( x ), чтобы определить наш(и) срез(ы). f ( x ) варьируется от 0 до ~0,1330, поэтому подойдет любое значение между этими двумя крайностями. Предположим, мы берем y = 0,1. Проблема в том, как отобрать точки, имеющие значения y > 0,1.
2. Далее мы устанавливаем наш параметр ширины w , который мы будем использовать для расширения нашей области рассмотрения. Это значение произвольно. Предположим, что w = 2.
3. Далее нам нужно начальное значение для x . Мы берем x из равномерного распределения в области f ( x ), которое удовлетворяет f ( x ) > 0,1 (наш параметр y ). Предположим, что x = 2. Это работает, потому что f (2) = ~0,1065 > 0,1. ^[8]
4. Поскольку x = 2 и w = 2, наша текущая область интереса ограничена (1, 3).
5. Теперь каждая конечная точка этой области проверяется на предмет того, лежит ли она за пределами заданного среза. Наша правая граница лежит за пределами нашего среза ( f (3) = ~0,0807 < 0,1), но левое значение — нет ( f (1) = ~0,1258 > 0,1). Мы расширяем левую границу, добавляя к ней w , пока она не выйдет за пределы среза. После этого процесса новые границы нашей области интереса будут (−3, 3).
6. Далее мы берем равномерный образец в пределах (−3, 3). Предположим, что этот образец дает x = −2,9. Хотя этот образец находится в пределах нашей области интереса, он не лежит в пределах нашего среза (f(2,9) = ~0,08334 < 0,1), поэтому мы изменяем левую границу нашей области интереса до этой точки. Теперь мы берем равномерный образец из (−2,9, 3). Предположим, что на этот раз наш образец дает x = 1, что находится в пределах нашего среза, и, таким образом, является принятым выходом образца с помощью выборки среза. Если бы наш новый x не находился в пределах нашего среза, мы бы продолжили процесс сжатия/повторной выборки до тех пор, пока не будет найден допустимый x в пределах границ.

Если нас интересует пик распределения, мы можем продолжать повторять этот процесс, поскольку новая точка соответствует более высокому значению f ( x ), чем исходная точка.

Для выборки из нормального распределения мы сначала выбираем начальное x — скажем, 0. После каждой выборки x мы выбираем y равномерно и случайно из , что ограничивает функцию распределения вероятностей . После каждой выборки y мы выбираем x равномерно и случайно из , где . Это срез, где .${\displaystyle N(0,1)}$${\displaystyle (0,e^{-x^{2}/2}/{\sqrt {2\pi }}]}$${\displaystyle N(0,1)}$${\displaystyle [-\alpha ,\alpha ]}$${\displaystyle \alpha ={\sqrt {-2\ln(y{\sqrt {2\pi }})}}}$${\displaystyle f(x)>y}$

Реализация на языке Macsyma :

срез ( x ) :=  блок ([ y ,  альфа ] ,  y: случайный ( exp ( - x ^ 2  /  2.0 ) /  sqrt ( 2.0  *  dfloat ( % пи ))) ,  альфа: sqrt ( -2.0  *  ln ( y  *  sqrt ( 2.0  *  dfloat ( % пи )))) ,  x: знак ( случайный ()) *  случайный ( альфа )) ;

• Марковская цепь Монте-Карло

• http://www.probability.ca/jeff/java/slice.html