Шерлет

В прикладном математическом анализе ширлеты представляют собой многомасштабную структуру, которая позволяет эффективно кодировать анизотропные признаки в многомерных классах задач. Первоначально ширлеты были введены в 2006 году [1] для анализа и разреженной аппроксимации функций . Они являются естественным расширением вейвлетов , чтобы учесть тот факт, что многомерные функции обычно управляются анизотропными признаками, такими как края в изображениях, поскольку вейвлеты, как изотропные объекты, не способны фиксировать такие явления. ф ∈ Л 2 ( Р 2 ) {\displaystyle f\in L^{2}(\mathbb {R} ^{2})}

Shearlets строятся путем параболического масштабирования , сдвига и перевода, применяемых к нескольким производящим функциям . В мелких масштабах они по существу поддерживаются тонкими и направленными гребнями, следующими закону параболического масштабирования, который гласит: длина² ≈ ширина . Подобно вейвлетам, shearlets возникают из аффинной группы и допускают унифицированную обработку континуума и цифровой ситуации, что приводит к точным реализациям. Хотя они не составляют ортонормальный базис для , они все же образуют фрейм, допускающий устойчивые расширения произвольных функций . Л 2 ( Р 2 ) {\displaystyle L^{2}(\mathbb {R} ^{2})} ф ∈ Л 2 ( Р 2 ) {\displaystyle f\in L^{2}(\mathbb {R} ^{2})}

Одним из важнейших свойств ширлетов является их способность обеспечивать оптимально разреженные приближения (в смысле оптимальности в [2] ) для карикатурных функций . В науках о визуализации карикатурные функции служат моделью для анизотропных признаков и компактно поддерживаются в , будучи отделенными от замкнутой кусочно- сингулярной кривой с ограниченной кривизной. Скорость затухания -ошибки -члена ширлет-приближения, полученного путем взятия наибольших коэффициентов из ширлет-разложения, на самом деле оптимальна с точностью до логарифмического фактора: [3] [4] ф {\displaystyle f} [ 0 , 1 ] 2 {\displaystyle [0,1]^{2}} С 2 {\displaystyle С^{2}} С 2 {\displaystyle С^{2}} Л 2 {\displaystyle L^{2}} Н {\displaystyle N} Н {\displaystyle N}

‖ ф − ф Н ‖ Л 2 2 ≤ С Н − 2 ( бревно ⁡ Н ) 3 , Н → ∞ , {\displaystyle \|f-f_{N}\|_{L^{2}}^{2}\leq CN^{-2}(\log N)^{3},\quad N\to \infty ,}

где константа зависит только от максимальной кривизны кривой сингулярности и максимальных величин , и . Такая скорость аппроксимации значительно улучшает скорость наилучшего -члена аппроксимации вейвлетов, предоставляемых только для такого класса функций. С {\displaystyle C} f {\displaystyle f} f ′ {\displaystyle f'} f ″ {\displaystyle f''} N {\displaystyle N} O ( N − 1 ) {\displaystyle O(N^{-1})}

Shearlets на сегодняшний день являются единственной системой направленного представления, которая обеспечивает разреженную аппроксимацию анизотропных характеристик, обеспечивая при этом унифицированную обработку континуума и цифровой области, что позволяет точную реализацию. Расширения систем shearlet также доступны. Полное представление теории и приложений shearlets можно найти в. [5] L 2 ( R d ) , d ≥ 2 {\displaystyle L^{2}(\mathbb {R} ^{d}),d\geq 2}

Определение

Непрерывные системы ширлетов

Геометрические эффекты параболического масштабирования и сдвига с несколькими параметрами a и s.

Построение непрерывных систем ширлетов основано на параболических масштабирующих матрицах.

A a = [ a 0 0 a 1 / 2 ] , a > 0 {\displaystyle A_{a}={\begin{bmatrix}a&0\\0&a^{1/2}\end{bmatrix}},\quad a>0}

как средство изменения разрешения, на матрицах сдвига

S s = [ 1 s 0 1 ] , s ∈ R {\displaystyle S_{s}={\begin{bmatrix}1&s\\0&1\end{bmatrix}},\quad s\in \mathbb {R} }

как средство изменения ориентации, и, наконец, на трансляциях для изменения позиционирования. По сравнению с curvellets , shearlets используют сдвиги вместо вращений, преимущество в том, что оператор сдвига оставляет целочисленную решетку инвариантной в случае , т. е. Это действительно позволяет унифицировать обработку континуума и цифровой области, тем самым гарантируя точную цифровую реализацию. S s {\displaystyle S_{s}} s ∈ Z {\displaystyle s\in \mathbb {Z} } S s Z 2 ⊆ Z 2 . {\displaystyle S_{s}\mathbb {Z} ^{2}\subseteq \mathbb {Z} ^{2}.}

Для непрерывной системы ширлет, генерируемой, определяется как ψ ∈ L 2 ( R 2 ) {\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})} ψ {\displaystyle \psi }

SH c o n t ⁡ ( ψ ) = { ψ a , s , t = a 3 / 4 ψ ( S s A a ( ⋅ − t ) ) ∣ a > 0 , s ∈ R , t ∈ R 2 } , {\displaystyle \operatorname {SH} _{\mathrm {cont} }(\psi )=\{\psi _{a,s,t}=a^{3/4}\psi (S_{s}A_{a}(\cdot -t))\mid a>0,s\in \mathbb {R} ,t\in \mathbb {R} ^{2}\},}

и соответствующее непрерывное преобразование ширлета задается отображением

f ↦ S H ψ f ( a , s , t ) = ⟨ f , ψ a , s , t ⟩ , f ∈ L 2 ( R 2 ) , ( a , s , t ) ∈ R > 0 × R × R 2 . {\displaystyle f\mapsto {\mathcal {SH}}_{\psi }f(a,s,t)=\langle f,\psi _{a,s,t}\rangle ,\quad f\in L^{2}(\mathbb {R} ^{2}),\quad (a,s,t)\in \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}

Дискретные системы ширлетов

Дискретную версию систем ширлетов можно получить непосредственно путем дискретизации набора параметров. Для этого существует множество подходов, но наиболее популярным является следующий: SH c o n t ⁡ ( ψ ) {\displaystyle \operatorname {SH} _{\mathrm {cont} }(\psi )} R > 0 × R × R 2 . {\displaystyle \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}

{ ( 2 j , k , A 2 j − 1 S k − 1 m ) ∣ j ∈ Z , k ∈ Z , m ∈ Z 2 } ⊆ R > 0 × R × R 2 . {\displaystyle \{(2^{j},k,A_{2^{j}}^{-1}S_{k}^{-1}m)\mid j\in \mathbb {Z} ,k\in \mathbb {Z} ,m\in \mathbb {Z} ^{2}\}\subseteq \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}

Исходя из этого, дискретная система ширлетов , связанная с генератором ширлетов, определяется как ψ {\displaystyle \psi }

SH ⁡ ( ψ ) = { ψ j , k , m = 2 3 j / 4 ψ ( S k A 2 j ⋅ − m ) ∣ j ∈ Z , k ∈ Z , m ∈ Z 2 } , {\displaystyle \operatorname {SH} (\psi )=\{\psi _{j,k,m}=2^{3j/4}\psi (S_{k}A_{2^{j}}\cdot {}-m)\mid j\in \mathbb {Z} ,k\in \mathbb {Z} ,m\in \mathbb {Z} ^{2}\},}

и соответствующее дискретное преобразование ширлета определяется как

f ↦ S H ψ f ( j , k , m ) = ⟨ f , ψ j , k , m ⟩ , f ∈ L 2 ( R 2 ) , ( j , k , m ) ∈ Z × Z × Z 2 . {\displaystyle f\mapsto {\mathcal {SH}}_{\psi }f(j,k,m)=\langle f,\psi _{j,k,m}\rangle ,\quad f\in L^{2}(\mathbb {R} ^{2}),\quad (j,k,m)\in \mathbb {Z} \times \mathbb {Z} \times \mathbb {Z} ^{2}.}

Примеры

Пусть — функция, удовлетворяющая дискретному условию Кальдерона , т.е. ψ 1 ∈ L 2 ( R ) {\displaystyle \psi _{1}\in L^{2}(\mathbb {R} )}

∑ j ∈ Z | ψ ^ 1 ( 2 − j ξ ) | 2 = 1 , for a.e.  ξ ∈ R , {\displaystyle \sum _{j\in \mathbb {Z} }|{\hat {\psi }}_{1}(2^{-j}\xi )|^{2}=1,{\text{for a.e. }}\xi \in \mathbb {R} ,}

с и где обозначает преобразование Фурье Например, можно выбрать вейвлет Мейера . Кроме того, пусть будет таким, что и ψ ^ 1 ∈ C ∞ ( R ) {\displaystyle {\hat {\psi }}_{1}\in C^{\infty }(\mathbb {R} )} supp ⁡ ψ ^ 1 ⊆ [ − 1 2 , − 1 16 ] ∪ [ 1 16 , 1 2 ] , {\displaystyle \operatorname {supp} {\hat {\psi }}_{1}\subseteq [-{\tfrac {1}{2}},-{\tfrac {1}{16}}]\cup [{\tfrac {1}{16}},{\tfrac {1}{2}}],} ψ ^ 1 {\displaystyle {\hat {\psi }}_{1}} ψ 1 . {\displaystyle \psi _{1}.} ψ 1 {\displaystyle \psi _{1}} ψ 2 ∈ L 2 ( R ) {\displaystyle \psi _{2}\in L^{2}(\mathbb {R} )} ψ ^ 2 ∈ C ∞ ( R ) , {\displaystyle {\hat {\psi }}_{2}\in C^{\infty }(\mathbb {R} ),} supp ⁡ ψ ^ 2 ⊆ [ − 1 , 1 ] {\displaystyle \operatorname {supp} {\hat {\psi }}_{2}\subseteq [-1,1]}

∑ k = − 1 1 | ψ ^ 2 ( ξ + k ) | 2 = 1 , for a.e.  ξ ∈ [ − 1 , 1 ] . {\displaystyle \sum _{k=-1}^{1}|{\hat {\psi }}_{2}(\xi +k)|^{2}=1,{\text{for a.e. }}\xi \in \left[-1,1\right].}

Обычно выбирается гладкая функция выпуклости . Тогда задается как ψ ^ 2 {\displaystyle {\hat {\psi }}_{2}} ψ ∈ L 2 ( R 2 ) {\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})}

ψ ^ ( ξ ) = ψ ^ 1 ( ξ 1 ) ψ ^ 2 ( ξ 2 ξ 1 ) , ξ = ( ξ 1 , ξ 2 ) ∈ R 2 , {\displaystyle {\hat {\psi }}(\xi )={\hat {\psi }}_{1}(\xi _{1}){\hat {\psi }}_{2}\left({\tfrac {\xi _{2}}{\xi _{1}}}\right),\quad \xi =(\xi _{1},\xi _{2})\in \mathbb {R} ^{2},}

называется классическим ширлетом . Можно показать, что соответствующая дискретная система ширлетов образует парсевалевский фрейм для функций с ограниченной полосой пропускания . [5] SH ⁡ ( ψ ) {\displaystyle \operatorname {SH} (\psi )} L 2 ( R 2 ) {\displaystyle L^{2}(\mathbb {R} ^{2})}

Другим примером являются компактно поддерживаемые системы ширлетов, где компактно поддерживаемая функция может быть выбрана так, что образует рамку для . [4] [6] [7] [8] В этом случае все элементы ширлетов в компактно поддерживаются, обеспечивая превосходную пространственную локализацию по сравнению с классическими ширлетами, которые ограничены полосой пропускания. Хотя компактно поддерживаемая система ширлетов обычно не образует рамку Парсеваля, любая функция может быть представлена ​​расширением ширлетов из-за ее свойства рамы. ψ ∈ L 2 ( R 2 ) {\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})} SH ⁡ ( ψ ) {\displaystyle \operatorname {SH} (\psi )} L 2 ( R 2 ) {\displaystyle L^{2}(\mathbb {R} ^{2})} SH ⁡ ( ψ ) {\displaystyle \operatorname {SH} (\psi )} f ∈ L 2 ( R 2 ) {\displaystyle f\in L^{2}(\mathbb {R} ^{2})}

Адаптированные к конусу ширлеты

Одним из недостатков ширлетов, определенных выше, является направленное смещение элементов ширлета, связанное с большими параметрами сдвига. Этот эффект уже заметен в частотной мозаике классических ширлетов (см. рисунок в разделе #Примеры), где поддержка частоты ширлета все больше выравнивается вдоль оси -, когда параметр сдвига стремится к бесконечности. Это вызывает серьезные проблемы при анализе функции, преобразование Фурье которой сосредоточено вокруг оси -. ξ 2 {\displaystyle \xi _{2}} s {\displaystyle s} ξ 2 {\displaystyle \xi _{2}}

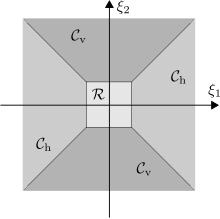
Разложение частотной области на конусы
Разложение частотной области на конусы.

Для решения этой проблемы частотная область делится на низкочастотную часть и две конические области (см. рисунок):

R = { ( ξ 1 , ξ 2 ) ∈ R 2 ∣ | ξ 1 | , | ξ 2 | ≤ 1 } , C h = { ( ξ 1 , ξ 2 ) ∈ R 2 ∣ | ξ 2 / ξ 1 | ≤ 1 , | ξ 1 | > 1 } , C v = { ( ξ 1 , ξ 2 ) ∈ R 2 ∣ | ξ 1 / ξ 2 | ≤ 1 , | ξ 2 | > 1 } . {\displaystyle {\begin{aligned}{\mathcal {R}}&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{1}|,|\xi _{2}|\leq 1\right\},\\{\mathcal {C}}_{\mathrm {h} }&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{2}/\xi _{1}|\leq 1,|\xi _{1}|>1\right\},\\{\mathcal {C}}_{\mathrm {v} }&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{1}/\xi _{2}|\leq 1,|\xi _{2}|>1\right\}.\end{aligned}}}
Частотная мозаика конусно-адаптированной системы ширлетов
Частотная мозаика конусно-адаптированной системы ширлетов, созданной классическим ширлетом.

Связанная с конусом адаптированная дискретная система shearlet состоит из трех частей, каждая из которых соответствует одной из этих частотных областей. Она генерируется тремя функциями и фактором выборки решетки ϕ , ψ , ψ ~ ∈ L 2 ( R 2 ) {\displaystyle \phi ,\psi ,{\tilde {\psi }}\in L^{2}(\mathbb {R} ^{2})} c = ( c 1 , c 2 ) ∈ ( R > 0 ) 2 : {\displaystyle c=(c_{1},c_{2})\in (\mathbb {R} _{>0})^{2}:}

SH ⁡ ( ϕ , ψ , ψ ~ ; c ) = Φ ( ϕ ; c 1 ) ∪ Ψ ( ψ ; c ) ∪ Ψ ~ ( ψ ~ ; c ) , {\displaystyle \operatorname {SH} (\phi ,\psi ,{\tilde {\psi }};c)=\Phi (\phi ;c_{1})\cup \Psi (\psi ;c)\cup {\tilde {\Psi }}({\tilde {\psi }};c),}

где

Φ ( ϕ ; c 1 ) = { ϕ m = ϕ ( ⋅ − c 1 m ) ∣ m ∈ Z 2 } , Ψ ( ψ ; c ) = { ψ j , k , m = 2 3 j / 4 ψ ( S k A 2 j ⋅ − M c m ) ∣ j ≥ 0 , | k | ≤ ⌈ 2 j / 2 ⌉ , m ∈ Z 2 } , Ψ ~ ( ψ ~ ; c ) = { ψ ~ j , k , m = 2 3 j / 4 ψ ( S ~ k A ~ 2 j ⋅ − M ~ c m ) ∣ j ≥ 0 , | k | ≤ ⌈ 2 j / 2 ⌉ , m ∈ Z 2 } , {\displaystyle {\begin{aligned}\Phi (\phi ;c_{1})&=\{\phi _{m}=\phi (\cdot {}-c_{1}m)\mid m\in \mathbb {Z} ^{2}\},\\\Psi (\psi ;c)&=\{\psi _{j,k,m}=2^{3j/4}\psi (S_{k}A_{2^{j}}\cdot {}-M_{c}m)\mid j\geq 0,|k|\leq \lceil 2^{j/2}\rceil ,m\in \mathbb {Z} ^{2}\},\\{\tilde {\Psi }}({\tilde {\psi }};c)&=\{{\tilde {\psi }}_{j,k,m}=2^{3j/4}\psi ({\tilde {S}}_{k}{\tilde {A}}_{2^{j}}\cdot {}-{\tilde {M}}_{c}m)\mid j\geq 0,|k|\leq \lceil 2^{j/2}\rceil ,m\in \mathbb {Z} ^{2}\},\end{aligned}}}

с

A ~ a = [ a 1 / 2 0 0 a ] , a > 0 , S ~ s = [ 1 0 s 1 ] , s ∈ R , M c = [ c 1 0 0 c 2 ] , and M ~ c = [ c 2 0 0 c 1 ] . {\displaystyle {\begin{aligned}&{\tilde {A}}_{a}={\begin{bmatrix}a^{1/2}&0\\0&a\end{bmatrix}},\;a>0,\quad {\tilde {S}}_{s}={\begin{bmatrix}1&0\\s&1\end{bmatrix}},\;s\in \mathbb {R} ,\quad M_{c}={\begin{bmatrix}c_{1}&0\\0&c_{2}\end{bmatrix}},\quad {\text{and}}\quad {\tilde {M}}_{c}={\begin{bmatrix}c_{2}&0\\0&c_{1}\end{bmatrix}}.\end{aligned}}}

Системы и в основном отличаются обратными ролями и . Таким образом, они соответствуют коническим областям и , соответственно. Наконец, масштабирующая функция связана с низкочастотной частью . Ψ ( ψ ) {\displaystyle \Psi (\psi )} Ψ ~ ( ψ ~ ) {\displaystyle {\tilde {\Psi }}({\tilde {\psi }})} x 1 {\displaystyle x_{1}} x 2 {\displaystyle x_{2}} C h {\displaystyle {\mathcal {C}}_{\mathrm {h} }} C v {\displaystyle {\mathcal {C}}_{\mathrm {v} }} ϕ {\displaystyle \phi } R {\displaystyle {\mathcal {R}}}

Приложения

Обобщения и расширения

  • 3D-Shearlets [7] [9]
  • α {\displaystyle \alpha } -Ширлеты [7]
  • Параболические молекулы [10]
  • Цилиндрические ширлеты [11] [12]

Смотрите также

Ссылки

  1. ^ Го, Кангхуи, Гитта Кутыниок и Деметрио Лабате. «Разреженные многомерные представления с использованием анизотропных операторов растяжения и сдвига». Вейвлеты и сплайны (Афины, Джорджия, 2005), G. Chen и MJ Lai, ред., Nashboro Press, Нэшвилл, Теннесси (2006): 189–201. «PDF» (PDF) .
  2. ^ Донохо, Дэвид Ли. «Разреженные компоненты изображений и оптимальные атомарные разложения». Constructive Approximation 17.3 (2001): 353–382. «PDF». CiteSeerX 10.1.1.379.8993 . 
  3. ^ Го, Кангхуэй и Деметрио Лабате. «Оптимально разреженное многомерное представление с использованием ширлетов». Журнал SIAM по математическому анализу 39.1 (2007): 298–318. «PDF» (PDF) .
  4. ^ ab Kutyniok, Gitta и Wang-Q Lim. «Компактно поддерживаемые ширлеты оптимально разрежены». Журнал теории аппроксимации 163.11 (2011): 1564–1589. «PDF» (PDF) .
  5. ^ abcde Kutyniok, Gitta и Demetrio Labate, ред. Shearlets: Многомасштабный анализ для многомерных данных . Springer, 2012, ISBN 0-8176-8315-1 
  6. ^ Kittipoom, Pisamai, Gitta Kutyniok и Wang-Q Lim. «Построение компактно поддерживаемых ширлет-рам». Constructive Approximation 35.1 (2012): 21–72. Kittipoom, P.; Kutyniok, G.; Lim, W. (2010). «PDF». arXiv : 1003.5481 [math.FA].
  7. ^ abc Kutyniok, Gitta , Jakob Lemvig и Wang-Q Lim. "Оптимально разреженные аппроксимации 3D-функций компактно поддерживаемыми ширлет-фреймами". SIAM Journal on Mathematical Analysis 44.4 (2012): 2962–3017. Kutyniok, Gitta; Lemvig, Jakob; Lim, Wang-Q (2011). "PDF". arXiv : 1109.5993 [math.FA].
  8. ^ Purnendu Banerjee и BB Chaudhuri, «Локализация видеотекста с использованием вейвлет- и ширлет-преобразований», в Proc. SPIE 9021, Document Recognition and Retrieval XXI, 2014 (doi:10.1117/12.2036077). Banerjee, Purnendu; Chaudhuri, BB (2013). «Локализация видеотекста с использованием вейвлет- и ширлет-преобразований». В Coüasnon, Bertrand; Ringger, Eric K (ред.). Document Recognition and Retrieval XXI . Vol. 9021. pp. 90210B. arXiv : 1307.4990 . doi :10.1117/12.2036077. S2CID  10659099.
  9. ^ Го, Кангхуэй и Деметрио Лабате. «Построение гладких парсевалевых рамок ширлетов». Математическое моделирование природных явлений 8.01 (2013): 82–105. «PDF» (PDF) .
  10. ^ Грохс, Филипп и Кутынёк, Гитта . "Параболические молекулы". Основы вычислительной математики (в печати) Грохс, Филипп; Кутынёк, Гитта (2012). "PDF". arXiv : 1206.1958 [math.FA].
  11. ^ Исли, Гленн Р.; Го, Канхуэй; Лабате, Деметрио; Пахари, Басанта Р. (10 августа 2020 г.). «Оптимально разреженное представление мультяшных цилиндрических данных». Журнал геометрического анализа . 39 (9): 8926–8946. дои : 10.1007/s12220-020-00493-0. S2CID  221675372 . Проверено 22 января 2022 г.
  12. ^ Бернхард, Бернхард Г.; Лабате, Деметрио; Пахари, Басанта Р. (2019-10-29). «Гладкие проекции и построение гладких парсевалевых фреймов ширлетов». Успехи вычислительной математики . 45 (5–6): 3241–3264. doi :10.1007/s10444-019-09736-3. S2CID  210118010. Получено 2022-01-22 .
  • Домашняя страница Гитты Кутынёк
  • Домашняя страница Деметрио Лабате
Retrieved from "https://en.wikipedia.org/w/index.php?title=Shearlet&oldid=1142635965"