Модуль сопротивления сечения
Геометрические свойства элемента конструкции

В механике твердого тела и строительной инженерии момент сопротивления сечения — это геометрическое свойство заданного поперечного сечения, используемое при проектировании балок или изгибаемых элементов . Другие геометрические свойства, используемые при проектировании, включают: площадь для растяжения и сдвига, радиус инерции для сжатия, а также момент инерции площади и полярный момент инерции площади для жесткости . Любая связь между этими свойствами в значительной степени зависит от рассматриваемой формы. Существует два типа модуля сопротивления сечения: упругий и пластичный:

  • Модуль упругости сечения используется для расчета сопротивления поперечного сечения изгибу в упругом диапазоне, где напряжение и деформация пропорциональны.
  • Пластический модуль сечения используется для расчета способности поперечного сечения противостоять изгибу после того, как текучесть произошла по всему сечению. Он используется для определения пластической прочности или прочности полного момента и больше, чем упругий модуль сечения, отражая прочность сечения за пределами упругого диапазона. [1]

Уравнения для модулей сечения обычных форм приведены ниже. Модули сечения для различных профилей часто доступны в виде числовых значений в таблицах, в которых перечислены свойства стандартных структурных форм. [2]

Примечание: Оба модуля упругого и пластического сечения отличаются от первого момента площади . Он используется для определения того, как распределяются силы сдвига.

Обозначение

В различных нормах используются различные обозначения для упругого и пластического модуля сопротивления сечения, как показано в таблице ниже.

Обозначение модуля сечения
ОбластьКодМодуль сечения
ЭластичныйПластик
Северная АмерикаСША: ANSI/AISC 360-10 [3]СЗ
Канада: CSA S16-14 [4]СЗ
ЕвропаЕвропа (включая Великобританию): Еврокод 3 [5]W elW пл.
Великобритания (устаревший): BS 5950 a [6]ЗС
АзияЯпония: Стандартные спецификации для стальных и композитных конструкций [7]ВтЗ
Китай: GB 50017 [8]ВтВт п
Индия: IS 800 [9]З еЗ п
Австралия: AS 4100 [10]ЗС
Примечания:

а) Отменен 30 марта 2010 года, вместо него используется Еврокод 3. [11]

В статье используется североамериканская нотация.

Упругий модуль сечения

Модуль упругости сечения используется для общего проектирования. Он применим до предела текучести для большинства металлов и других распространенных материалов. Он определяется как [1]

С = я с {\displaystyle S={\frac {I}{c}}}

где:

I — второй момент площади (или момент инерции площади, не путать с моментом инерции ), и
c — расстояние от нейтральной оси до самого крайнего волокна.

Используется для определения момента текучести сечения [1]

М у = С ⋅ σ у {\displaystyle M_{y}=S\cdot \sigma _{y}}

где σ y — предел текучести материала.

В таблице ниже приведены формулы для расчета модуля упругости сечения для различных форм.

Уравнения модуля упругого сечения
Форма поперечного сеченияФигураУравнениеКомментарийСсылка.
Прямоугольник С = б час 2 6 {\displaystyle S={\cfrac {bh^{2}}{6}}} Сплошная стрелка представляет нейтральную ось[1]
Двойная симметрия Ɪ-сечение (большая ось) С х = Б ЧАС 2 6 − б час 3 6 ЧАС {\displaystyle S_{x}={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}}

С х = я х у {\displaystyle S_{x}={\tfrac {I_{x}}{y}}} ,

с у = ЧАС 2 {\displaystyle y={\cfrac {H}{2}}}

NA обозначает нейтральную ось[12]
Двойная симметрия Ɪ-сечение (малая ось) С у = Б 2 ( ЧАС − час ) 6 + ( Б − б ) 3 час 6 Б {\displaystyle S_{y}={\cfrac {B^{2}(Hh)}{6}}+{\cfrac {(Bb)^{3}h}{6B}}} NA обозначает нейтральную ось[13]
Круг С = π г 3 32 {\displaystyle S={\cfrac {\pi d^{3}}{32}}} Сплошная стрелка представляет нейтральную ось[12]
Круглое полое сечение 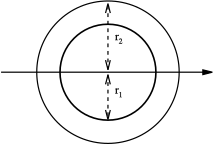С = π ( г 2 4 − г 1 4 ) 4 г 2 = π ( г 2 4 − г 1 4 ) 32 г 2 {\displaystyle S={\cfrac {\pi \left(r_{2}^{4}-r_{1}^{4}\right)}{4r_{2}}}={\cfrac {\pi (d_{2}^{4}-d_{1}^{4})}{32d_{2}}}} Сплошная стрелка представляет нейтральную ось[12]
Прямоугольное полое сечение 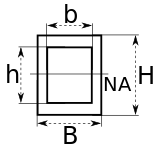С = Б ЧАС 2 6 − б час 3 6 ЧАС {\displaystyle S={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}} NA обозначает нейтральную ось[12]
Алмазный С = Б ЧАС 2 24 {\displaystyle S={\cfrac {BH^{2}}{24}}} NA обозначает нейтральную ось[12]
C-канал 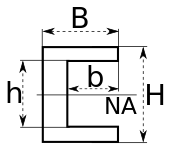С = Б ЧАС 2 6 − б час 3 6 ЧАС {\displaystyle S={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}} NA обозначает нейтральную ось[12]
Равные и неравные

Углы

Эти разделы требуют тщательного рассмотрения, поскольку оси для максимума и минимума

Момент сопротивления сечения не параллелен его полкам. [14] Доступны таблицы значений для стандартных сечений. [15]

[14]

[15]

Модуль упругости пластического сечения

Пластический модуль сечения используется для материалов и конструкций, где допустима ограниченная пластическая деформация. Он представляет собой способность сечения противостоять изгибу после того, как материал поддался и вошел в пластический диапазон. Он используется для определения пластической или полной прочности сечения на момент [1]

М п = З ⋅ σ у {\displaystyle M_{p}=Z\cdot \sigma _{y}}

где σ y — предел текучести материала.

Инженеры часто сравнивают прочность пластического момента с факторизованными приложенными моментами, чтобы убедиться, что конструкция может безопасно выдерживать требуемые нагрузки без значительной или неприемлемой постоянной деформации. Это неотъемлемая часть метода проектирования предельного состояния .

Пластический модуль сечения зависит от расположения пластической нейтральной оси (PNA). PNA определяется как ось, которая делит поперечное сечение таким образом, что сила сжатия от области сжатия равна силе растяжения от области растяжения. Для сечений с постоянным, равным пределом текучести при сжатии и растяжении , площадь выше и ниже PNA будет одинаковой [16]

А С = А Т {\displaystyle A_{C}=A_{T}}

Эти области могут различаться в композитных сечениях, имеющих разные свойства материалов, что приводит к неравному вкладу в модуль пластического сечения.

Пластический модуль сопротивления сечения рассчитывается как сумма площадей поперечного сечения по обе стороны от PNA, умноженных на расстояние от соответствующих локальных центроидов до PNA. [16]

З = А С у С + А Т у Т {\displaystyle Z=A_{C}y_{C}+A_{T}y_{T}}

где:

A C — площадь сжатия
A T — площадь в напряженном состоянии
y C , y T — расстояния от PNA до их центроидов.

Пластический момент сопротивления сечения и упругий момент сопротивления сечения можно связать с помощью коэффициента формы k :

к = М п М у = З С {\displaystyle k={\frac {M_{p}}{M_{y}}}={\frac {Z}{S}}}

Это показатель способности сечения выходить за пределы предела текучести материала. Коэффициент формы для прямоугольного сечения равен 1,5. [1]

В таблице ниже приведены формулы для расчета пластического модуля сопротивления сечения для различных форм.

Уравнения модуля пластического сечения
ОписаниеФигураУравнениеКомментарийСсылка.
Прямоугольное сечение З = б час 2 4 {\displaystyle Z={\frac {bh^{2}}{4}}}
А С = А Т = б час 2 {\displaystyle A_{C}=A_{T}={\frac {bh}{2}}} у С = у Т = час 4 {\displaystyle y_{C}=y_{T}={\frac {h}{4}}} [1]

[17]

Прямоугольное полое сечение З = б час 2 4 − ( б − 2 т ) ( час 2 − т ) 2 {\displaystyle Z={\cfrac {bh^{2}}{4}}-(b-2t)\left({\cfrac {h}{2}}-t\right)^{2}} b = ширина,
h = высота,
t = толщина стенки		[1]
Для двух полок двутавровой балки без стенки З = б 1 т 1 у 1 + б 2 т 2 у 2 {\displaystyle Z=b_{1}t_{1}y_{1}+b_{2}t_{2}y_{2}\,} b 1 , b 2 = ширина,
t 1 , t 2 = толщина,
y 1 , y 2 = расстояния от нейтральной оси до центров тяжести фланцев соответственно.		[18]
Для двутавровой балки, включая паутину Z = b t f ( d − t f ) + t w ( d − 2 t f ) 2 4 {\displaystyle Z=bt_{f}(d-t_{f})+{\frac {t_{w}(d-2t_{f})^{2}}{4}}} [1]

[19]

Для двутавровой балки (слабая ось) Z = b 2 t f 2 + t w 2 ( d − 2 t f ) 4 {\displaystyle Z={\frac {b^{2}t_{f}}{2}}+{\frac {t_{w}^{2}(d-2t_{f})}{4}}} d = полная высота двутавровой балки[1]
Закрашенный круг Z = d 3 6 {\displaystyle Z={\cfrac {d^{3}}{6}}} [1]
Круглое полое сечение Z = d 2 3 − d 1 3 6 {\displaystyle Z={\cfrac {d_{2}^{3}-d_{1}^{3}}{6}}} [1]
Равные и неравные углыЭти разделы требуют тщательного рассмотрения, поскольку оси для максимума и минимума

Момент сопротивления сечения не параллелен его полкам. [14]

[14]

Использование в строительной инженерии

В структурной инженерии выбор между использованием упругой или пластической (полный момент) прочности сечения определяется конкретным применением. Инженеры следуют соответствующим нормам, которые диктуют, является ли упругий или пластический подход к проектированию подходящим, что в свою очередь информирует об использовании упругого или пластического модуля сечения. Хотя подробное рассмотрение всех соответствующих норм выходит за рамки данной статьи, следующие замечания заслуживают внимания:

  • При оценке прочности длинных тонких балок важно оценить их способность противостоять поперечному изгибу при кручении , а также определить их моментную способность на основе модуля сопротивления сечения. [20]
  • Хотя Т-образные сечения могут быть не самым эффективным выбором для сопротивления изгибу, их иногда выбирают из-за их архитектурной привлекательности. В таких случаях крайне важно тщательно оценить их способность противостоять боковому торсионному выпучиванию . [21]
  • Хотя стандартные балки с одинаковым поперечным сечением часто используются, они могут не быть оптимально использованы при воздействии моментов нагрузки, которые изменяются по их длине. Для больших балок с предсказуемыми условиями нагрузки стратегическая регулировка модуля сечения по длине может значительно повысить эффективность и рентабельность. [22]
  • В некоторых приложениях, таких как краны и авиационные или космические конструкции, полагаться исключительно на расчеты часто считается недостаточным. В этих случаях проводятся структурные испытания для подтверждения грузоподъемности конструкции.

Смотрите также

Ссылки

  1. ^ abcdefghijkl Янг, Уоррен К. (1989). Формулы Рорка для напряжения и деформации (PDF) . McGraw Hill. стр. 217.
  2. ^ "Главная страница 'Blue Book' - Blue Book - Steel for Life". www.steelforlifebluebook.co.uk . Получено 25.08.2024 .
  3. ^ "Спецификация для зданий из конструкционной стали (ANSI/AISC 360-10) - 2010 | Американский институт стальных конструкций". www.aisc.org . Получено 2024-08-23 .
  4. ^ S16-14 (R2019) Проектирование стальных конструкций . Канадская ассоциация стандартов. 2024-08-23.
  5. ^ Еврокод 3: Проектирование стальных конструкций. Часть 1-1: Общие правила и правила для зданий . ISBN 978 0 539 13167 3.
  6. ^ BS 5950-1 Конструктивное использование стальных конструкций в строительстве, BSI British Standards , получено 23 августа 2024 г.
  7. ^ Стандартные спецификации для стальных и композитных конструкций (первое издание). Япония: Японское общество инженеров-строителей (опубликовано в декабре 2009 г.). 2024-08-24.
  8. ^ GB 50017 Кодекс проектирования стальных конструкций . Китай: Министерство строительства Китайской Народной Республики (опубликовано 25.04.2003). 2003.
  9. ^ IS800:2007 Общее строительство из стали. Свод правил (Третье изд.). Индия: Бюро индийских стандартов (опубликовано в 2017 г.). 2007.
  10. ^ AS 4100- 2020 Стальные конструкции . Австралия: Standards Australia Ltd. 2020. ISBN 978 1 76072 947 9.
  11. ^ "Британский институт стандартов". 2024-08-23 . Получено 2024-08-23 .
  12. ^ abcdef Гир, Дж. М. и Тимнко, С., 1997, Механика материалов, 4-е изд., PWS Publishing Co.
  13. ^ «Уравнения и калькуляторы модуля сопротивления сечения. Общие формы».
  14. ^ abcd Trahair, NS (2002-11-01). "Моментные мощности стальных уголковых секций". Журнал структурной инженерии . 128 (11): 1387– 1393. doi :10.1061/(asce)0733-9445(2002)128:11(1387). ISSN  0733-9445.
  15. ^ ab "Свойства сечения - Размеры и свойства - Синяя книга - Сталь для жизни". www.steelforlifebluebook.co.uk . Получено 2024-08-27 .
  16. ^ ab "Пластический модуль" (PDF) .
  17. ^ "Расчет момента сопротивления сечения".
  18. ^ Американский институт стальных конструкций: Расчет нагрузки и коэффициента сопротивления, 3-е издание, стр. 17-34.
  19. ^ Мегсон, THG (2005). Структурный и напряженный анализ. elsever. стр. 598 EQ (iv). ISBN 9780080455341.
  20. ^ Брокенбро, Роджер Л.; Мерритт, Фредерик С., ред. (1999). Справочник проектировщика стальных конструкций . Справочники McGraw-Hill (3-е изд.). Нью-Йорк: McGraw-Hill. стр. 3.96. ISBN 978-0-07-008782-8.
  21. ^ Браун, Дэвид (2024-08-27). "Проектирование тавровых профилей при изгибе" (PDF) . Новые стальные конструкции .
  22. ^ Vu, Huy Hoang; Chu, Thi Hoang Anh (2024). "Сравнение оптимизации просто поддерживаемых составных двутавровых балок". E3S Web of Conferences . 533 : 02010. doi : 10.1051/e3sconf/202453302010 . ISSN  2267-1242.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Section_modulus&oldid=1247978042"