Список вторых моментов площади

Ниже приведен список вторых моментов площади некоторых фигур. Второй момент площади , также известный как момент инерции площади, является геометрическим свойством площади, которое отражает, как ее точки распределены относительно произвольной оси. Единицей измерения второго момента площади является длина в четвертой степени, L ⁴ , и ее не следует путать с моментом инерции массы . Однако, если деталь тонкая, момент инерции массы равен плотности площади , умноженной на момент инерции площади.

Обратите внимание, что для уравнений второго момента площади в таблице ниже: и$${\displaystyle I_{x}=\iint _{A}y^{2}\,dx\,dy}$$$${\displaystyle I_{y}=\iint _{A}x^{2}\,dx\,dy.}$$

Описание	Фигура	Второй момент площади	Комментарий
Заполненная круглая область радиуса r		${\displaystyle {\begin{align}I_{x}&={\frac {\pi }{4}}r^{4}\\[3pt]I_{y}&={\frac {\pi }{4}}r^{4}\\[3pt]I_{z}&={\frac {\pi }{2}}r^{4}\end{align}}}$ [1]	${\displaystyle I_{z}}$— второй полярный момент площади .
Кольцо с внутренним радиусом r 1 и внешним радиусом r 2		${\displaystyle {\begin{aligned}I_{x}&={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\\[3pt]I_{y}&={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\\[3pt]I_{z}&={\frac {\pi }{2}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\end{aligned}}}$	Для тонких трубок, и и так до первого порядка по , . Таким образом, для тонкой трубки, и .${\displaystyle r\equiv r_{1}\approx r_{2}}$${\displaystyle r_{2}\equiv r_{1}+t}$${\displaystyle т}$${\displaystyle r_{2}^{4}=r_{1}^{4}+4r_{1}^{3}t+\cdots }$${\displaystyle I_{x}=I_{y}\approx \pi r^{3}t}$${\displaystyle I_{z}\approx 2\pi r^{3}t}$ ${\displaystyle I_{z}}$— второй полярный момент площади .
Заполненный круговой сектор с углом θ в радианах и радиусом r относительно оси, проходящей через центр тяжести сектора и центр окружности		${\displaystyle I_{x}=\left(\theta -\sin \theta \right){\frac {r^{4}}{8}}}$	Эта формула верна только для 0 ≤ ≤${\textstyle \тета}$${\textstyle 2\пи}$
Заполненный полукруг радиусом r относительно горизонтальной линии, проходящей через центр тяжести области		${\displaystyle {\begin{aligned}I_{x}&=\left({\frac {\pi }{8}}-{\frac {8}{9\pi }}\right)r^{4}\approx 0.1098r^{4}\\[3pt]I_{y}&={\frac {\pi r^{4}}{8}}\end{aligned}}}$ [2]
Заполненный полукруг, как и выше, но относительно оси, коллинеарной с основанием		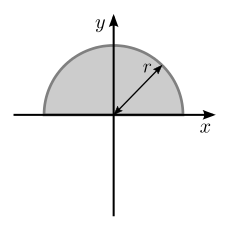${\displaystyle {\begin{align}I_{x}&={\frac {\pi r^{4}}{8}}\\[3pt]I_{y}&={\frac {\pi r^{4}}{8}}\end{align}}}$ [2]	${\displaystyle I_{x}}$: Это следствие теоремы о параллельных осях и того факта, что расстояние между осями x предыдущей и этой равно${\textstyle {\frac {4r}{3\pi }}}$
Заполненная четверть круга радиусом r с осями, проходящими через основания		${\displaystyle {\begin{align}I_{x}&={\frac {\pi r^{4}}{16}}\\[3pt]I_{y}&={\frac {\pi r^{4}}{16}}\end{align}}}$ [3]
Заполненная четверть круга радиусом r с осями, проходящими через центр тяжести		${\displaystyle {\begin{aligned}I_{x}&=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r^{4}\approx 0.0549r^{4}\\[3pt]I_{y}&=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r^{4}\approx 0.0549r^{4}\end{aligned}}}$ [3]	Это является следствием теоремы о параллельных осях и того факта, что расстояние между этими двумя осями равно${\textstyle {\frac {4r}{3\pi }}}$
Заполненный эллипс , радиус которого по оси x равен a , а радиус по оси y равен b.		${\displaystyle {\begin{align}I_{x}&={\frac {\pi }{4}}ab^{3}\\[3pt]I_{y}&={\frac {\pi }{4}}a^{3}b\end{align}}}$
Заполненная прямоугольная область с шириной основания b и высотой h		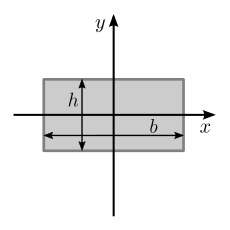${\displaystyle {\begin{align}I_{x}&={\frac {bh^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h}{12}}\end{align}}}$ [4]
Заполненная прямоугольная область, как указано выше, но относительно оси, коллинеарной с основанием.		${\displaystyle {\begin{align}I_{x}&={\frac {bh^{3}}{3}}\\[3pt]I_{y}&={\frac {b^{3}h}{3}}\end{align}}}$ [4]	Это результат теоремы о параллельных осях.
Полый прямоугольник с внутренним прямоугольником, ширина которого b 1 , а высота h 1		${\displaystyle {\begin{align}I_{x}&={\frac {bh^{3}-b_{1}{h_{1}}^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h-{b_{1}}^{3}h_{1}}{12}}\end{align}}}$
Заполненная треугольная область с шириной основания b , высотой h и смещением верхней вершины a относительно оси, проходящей через центр масс.		${\displaystyle {\begin{aligned}I_{x}&={\frac {bh^{3}}{36}}\\[3pt]I_{y}&={\frac {b^{3}hb^{2}ha+bha^{2}}{36}}\\[3pt]I_{xy}&=-{\frac {bh^{2}}{72}}(b-2a)\end{aligned}}}$ [5]
Заполненная треугольная область, как указано выше, но относительно оси, коллинеарной с основанием.		${\displaystyle {\begin{align}I_{x}&={\frac {bh^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h+b^{2}ha+bha^{2}}{12}}\end{align}}}$ [5]	Это следствие теоремы о параллельных осях.
Равнополочный уголок, часто встречающийся в инженерных приложениях.		${\displaystyle {\begin{aligned}I_{x}=I_{y}&={\frac {t(5L^{2}-5Lt+t^{2})(L^{2}-Lt+t^{2})}{12(2L-t)}}\\[3pt]I_{(xy)}&={\frac {L^{2}t(L-t)^{2}}{4(t-2L)}}\\[3pt]I_{a}&={\frac {t(2L-t)(2L^{2}-2Lt+t^{2})}{12}}\\[3pt]I_{b}&={\frac {t(2L^{4}-4L^{3}t+8L^{2}t^{2}-6Lt^{3}+t^{4})}{12(2L-t)}}\end{aligned}}}$	${\displaystyle I_{(xy)}}$часто не используемый «момент второго порядка площади», используемый для определения главных осей

Правильные многоугольники
Описание	Фигура	Второй момент площади	Комментарий
Заполненный правильный (равносторонний) треугольник со стороной длиной		${\displaystyle {\begin{aligned}I_{x}&={\frac {a^{4}}{32{\sqrt {3}}}}\approx 0.01804a^{4}\\[3pt]I_{y}&={\frac {a^{4}}{32{\sqrt {3}}}}\approx 0.01804a^{4}\end{aligned}}}$ [6]	Результат верен как для горизонтальной, так и для вертикальной оси, проходящей через центроид, и, следовательно, верен также для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников .
Закрашенный квадрат со стороной длиной а		${\displaystyle {\begin{aligned}I_{x}&={\frac {a^{4}}{12}}\\[3pt]I_{y}&={\frac {a^{4}}{12}}\end{aligned}}}$[6]	Результат верен как для горизонтальной, так и для вертикальной оси, проходящей через центроид, и, следовательно, верен также для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников .
Заполненный правильный шестиугольник с длиной стороны		${\displaystyle {\begin{aligned}I_{x}&={\frac {5{\sqrt {3}}}{16}}a^{4}\approx 0.54126a^{4}\\[3pt]I_{y}&={\frac {5{\sqrt {3}}}{16}}a^{4}\approx 0.54126a^{4}\end{aligned}}}$[6]	Результат верен как для горизонтальной, так и для вертикальной оси, проходящей через центроид, и, следовательно, верен также для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников .
Заполненный правильный восьмиугольник с длиной стороны		${\displaystyle {\begin{aligned}I_{x}&={\frac {11+8{\sqrt {2}}}{12}}a^{4}\approx 1.85947a^{4}\\[3pt]I_{y}&={\frac {11+8{\sqrt {2}}}{12}}a^{4}\approx 1.85947a^{4}\end{aligned}}}$[6]	Результат верен как для горизонтальной, так и для вертикальной оси, проходящей через центроид, и, следовательно, верен также для оси с произвольным направлением, проходящей через начало координат. Это справедливо для всех правильных многоугольников .

Теорему о параллельных осях можно использовать для определения момента инерции площади твердого тела относительно любой оси, если известны момент инерции площади тела относительно параллельной оси, проходящей через центр тяжести тела, площадь поперечного сечения и перпендикулярное расстояние ( d ) между осями.

$${\displaystyle I_{x'}=I_{x}+Ad^{2}}$$

• Список моментов инерции
• Список центроидов
• Второй полярный момент площади