Диаграмма рассеяния
Постройте график, используя дисперсию разбросанных точек, чтобы показать взаимосвязь между переменными.
Диаграмма рассеяния
Один из семи основных инструментов качества
Впервые описанДжон Гершель
ЦельОпределить тип взаимосвязи (если таковая имеется) между двумя количественными переменными
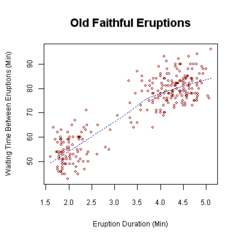
Время ожидания между извержениями и продолжительность извержения гейзера Old Faithful в Йеллоустонском национальном парке , Вайоминг , США. Эта диаграмма показывает, что в целом существует два типа извержений: короткое-ожидание-короткая-длительность и долгое-ожидание-длительная-длительность.
3D-диаграмма рассеяния позволяет визуализировать многомерные данные. Эта диаграмма рассеяния берет несколько скалярных переменных и использует их для разных осей в фазовом пространстве. Различные переменные объединяются для формирования координат в фазовом пространстве, и они отображаются с помощью глифов и раскрашиваются с помощью другой скалярной переменной. [1]

Диаграмма рассеяния , также называемая диаграммой рассеяния , графиком рассеяния , диаграммой рассеяния , диаграммой рассеяния или диаграммой рассеяния , [2] — это тип графика или математической диаграммы, использующей декартовы координаты для отображения значений, как правило, двух переменных для набора данных. Если точки закодированы (цвет/форма/размер), может быть отображена одна дополнительная переменная. Данные отображаются в виде набора точек, каждая из которых имеет значение одной переменной, определяющей положение на горизонтальной оси, и значение другой переменной, определяющей положение на вертикальной оси . [3]

История

По словам Майкла Френдли и Дэниела Дениса, определяющей характеристикой, отличающей диаграммы рассеяния от линейных диаграмм, является представление конкретных наблюдений двумерных данных, где одна переменная отображается на горизонтальной оси, а другая на вертикальной. Эти две переменные часто абстрагируются от физического представления, например, разброса пуль по цели или географической или небесной проекции. [4] [5]

Хотя Эдмунд Галлей создал двумерный график температуры и давления в 1686 году, он опустил конкретные точки данных, используемые для демонстрации этой связи. Френдли и Денис утверждают, что его визуализация отличалась от фактического графика рассеяния. Френдли и Денис приписывают первый график рассеяния Джону Гершелю . В 1833 году Гершель нанес на график угол между центральной звездой в созвездии Девы и Гаммой Девы с течением времени, чтобы выяснить, как угол изменяется со временем, не с помощью расчета, а с помощью рисования от руки и человеческого суждения. [4]

Сэр Фрэнсис Гальтон расширил и популяризировал диаграмму рассеяния и многие другие статистические инструменты для научного обоснования евгеники. [6] Когда в 1886 году Гальтон опубликовал диаграмму рассеяния и корреляционный эллипс роста родителей и детей, он расширил простое построение Гершелем точек данных, объединив и усреднив соседние ячейки, чтобы создать более гладкую визуализацию. [4] Карл Пирсон, Р. А. Фишер и другие статистики и евгеники основывались на работе Гальтона и формализовали корреляции и проверку значимости. [6]

Обзор

Диаграмма рассеяния может использоваться либо когда одна непрерывная переменная находится под контролем экспериментатора, а другая зависит от нее, либо когда обе непрерывные переменные независимы. Если существует параметр , который систематически увеличивается и/или уменьшается другим, он называется контрольным параметром или независимой переменной и обычно наносится на горизонтальную ось. Измеряемая или зависимая переменная обычно наносится на вертикальную ось. Если зависимой переменной не существует, любой тип переменной может быть нанесен на любую из осей, и диаграмма рассеяния будет иллюстрировать только степень корреляции ( не причинно-следственной связи ) между двумя переменными. [ необходима цитата ]

Диаграмма рассеяния может предполагать различные виды корреляций между переменными с определенным доверительным интервалом . Например, вес и рост будут находиться на оси Y , а рост будет находиться на оси X. Корреляции могут быть положительными (растущими), отрицательными (падающими) или нулевыми (некоррелированными). Если рисунок точек наклонен от нижнего левого угла к верхнему правому, это указывает на положительную корреляцию между изучаемыми переменными. Если рисунок точек наклонен от верхнего левого угла к нижнему правому, это указывает на отрицательную корреляцию. Линию наилучшего соответствия (альтернативно называемую «линией тренда») можно нарисовать для изучения взаимосвязи между переменными. Уравнение для корреляции между переменными можно определить с помощью установленных процедур наилучшего соответствия. Для линейной корреляции процедура наилучшего соответствия известна как линейная регрессия и гарантированно генерирует правильное решение за конечное время. Ни одна универсальная процедура наилучшего соответствия не гарантирует генерации правильного решения для произвольных взаимосвязей. Диаграмма рассеяния также очень полезна, когда мы хотим увидеть, как два сопоставимых набора данных согласуются, чтобы показать нелинейные взаимосвязи между переменными. Возможность сделать это можно улучшить, добавив плавную линию, такую ​​как LOESS . [7] Кроме того, если данные представлены смешанной моделью простых отношений, эти отношения будут визуально очевидны в виде наложенных друг на друга узоров. [ необходима цитата ]

Диаграмма рассеяния является одним из семи основных инструментов контроля качества . [8]

Диаграммы рассеяния могут быть построены в виде пузырьковых , маркерных и/или линейных диаграмм . [9]

Пример

Например, чтобы отобразить связь между объемом легких человека и тем, как долго этот человек может задерживать дыхание, исследователь выбирает группу людей для изучения, затем измеряет объем легких каждого из них (первая переменная) и то, как долго этот человек может задерживать дыхание (вторая переменная). Затем исследователь наносит данные на диаграмму рассеяния, присваивая «объем легких» горизонтальной оси, а «время задержки дыхания» — вертикальной оси. [ необходима цитата ]

Человек с объемом легких400  cl, которые затаили дыхание21,7 с будет представлено одной точкой на диаграмме рассеяния в точке (400, 21,7) в декартовых координатах . Диаграмма рассеяния всех людей в исследовании позволит исследователю получить визуальное сравнение двух переменных в наборе данных и поможет определить, какой тип связи может быть между двумя переменными. [ необходима цитата ]

Матрицы диаграмм рассеяния

Для набора переменных данных (измерений) X 1 , X 2 , ... , X k матрица диаграммы рассеяния показывает все попарные диаграммы рассеяния переменных в одном представлении с несколькими диаграммами рассеяния в матричном формате. Для k переменных матрица диаграммы рассеяния будет содержать k строк и k столбцов. График, расположенный на пересечении строки и j- го столбца, является графиком переменных X i в зависимости от X j . [10] Это означает, что каждая строка и столбец представляют собой одно измерение, а каждая ячейка отображает диаграмму рассеяния двух измерений. [ необходима цитата ]

Обобщенная матрица диаграммы рассеяния [11] предлагает ряд отображений парных комбинаций категориальных и количественных переменных. Мозаичный график , флуктуационная диаграмма или фасетная столбчатая диаграмма могут использоваться для отображения двух категориальных переменных. Другие графики используются для одной категориальной и одной количественной переменной.

Визуализация трехмерных данных вместе с соответствующей матрицей диаграммы рассеяния

Смотрите также

Ссылки

  1. ^ Визуализации, созданные с помощью VisIt на wci.llnl.gov. Последнее обновление: 8 ноября 2007 г.
  2. ^ Джаррелл, Стивен Б. (1994). Базовая статистика (специальное предпечатное издание). Дубьюк, Айова: Wm. C. Brown Pub. стр. 492. ISBN 978-0-697-21595-6. Когда мы ищем связь между двумя количественными переменными, стандартный график имеющихся пар данных (X,Y), называемый диаграммой рассеяния , часто помогает...
  3. ^ Уттс, Джессика М. Видение статистики , 3-е издание, Томсон Брукс/Коул, 2005, стр. 166-167. ISBN 0-534-39402-7 
  4. ^ abc Friendly, Michael; Denis, Dan (2005). «Ранние истоки и развитие диаграммы рассеяния». Журнал истории поведенческих наук . 41 (2): 103–130 . doi :10.1002/jhbs.20078. PMID  15812820.
  5. ^ "Ранние истоки и развитие диаграммы рассеяния" (PDF) . Архивировано из оригинала (PDF) 2010-06-13.
  6. ^ ab Louçã, Francisco (2009). «Эмансипация через взаимодействие — как евгеника и статистика сходились и расходились». Журнал истории биологии . 42 (4): 649– 684. doi :10.1007/s10739-008-9167-7. ISSN  0022-5010. JSTOR  25650625. PMID  20481126.
  7. ^ Кливленд, Уильям (1993). Визуализация данных . Мюррей Хилл, Нью-Джерси Саммит, Нью-Джерси: At & T Bell Laboratories Опубликовано Hobart Press. ISBN 978-0963488404.
  8. ^ Нэнси Р. Тейг (2004). "Семь основных инструментов качества". Набор инструментов качества . Милуоки, Висконсин : Американское общество качества . стр. 15. Получено 2010-02-05 .
  9. ^ "Scatter Chart – AnyChart JavaScript Chart Documentation". AnyChart. Архивировано из оригинала 1 февраля 2016 года . Получено 3 февраля 2016 года .
  10. ^ Матрица диаграммы рассеяния на itl.nist.gov.
  11. ^ Эмерсон, Джон В.; Грин, Уолтон А.; Шорке, Баррет; Кроули, Джейсон (2013). «Обобщенный парный график». Журнал вычислительной и графической статистики . 22 (1): 79– 91. doi :10.1080/10618600.2012.694762. S2CID  28344569.

Дальнейшее чтение

  • Каттанео, Матиас Д.; Крамп, Ричард К.; Фаррелл, Макс Х.; Фэн, Инцзе (2024). «О мусорном ведре». American Economic Review . 114 (5): 1488–1514.
  • Медиа, связанные с Scatterplots на Wikimedia Commons
  • Что такое диаграмма рассеивания? Архивировано 2020-08-07 в Wayback Machine
  • Матрица диаграммы рассеяния корреляции для упорядоченных категориальных данных – Пояснение и код R
  • Диаграмма рассеяния плотности для больших наборов данных (сотни миллионов точек)
Взято с "https://en.wikipedia.org/w/index.php?title=Scatter_plot&oldid=1269057708"