Ротонда (геометрия)
| Набор ротонд | |
|---|---|
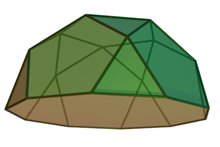 (Пример: пятиугольная ротонда ) | |
| Лица | 1 n -угольник 1 2 n -угольник n пятиугольников 2 n треугольников |
| Края | 7 н |
| Вершины | 4 н |
| Группа симметрии | C n v , [ n ], (* nn ), порядок 2 n |
| Группа вращения | C n , [n] + , ( nn ), порядок n |
| Характеристики | выпуклый |
В геометрии ротонда — это любой член семейства двугранно-симметричных многогранников . Они похожи на купол , но вместо чередующихся квадратов и треугольников, они чередуют пятиугольники и треугольники вокруг оси. Пятиугольная ротонда — это тело Джонсона .
Другие формы могут быть получены с помощью двугранной симметрии и искаженных равносторонних пятиугольников. [ нужен пример ]
Примеры
| 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
 треугольная ротонда |  квадратная ротонда |  пятиугольная ротонда |  шестиугольная ротонда |  семиугольная ротонда |  восьмиугольная ротонда |
Звезда-ротонда
| 5 | 7 | 9 | 11 |
|---|---|---|---|
 Пентаграммная ротонда |  Гептаграммовая ротонда |  Эннеаграммная ротонда |  Хендекаграммическая ротонда |
Смотрите также
Ссылки
- Норман В. Джонсон , «Выпуклые тела с правильными гранями», Канадский журнал математики, 18 , 1966, страницы 169–200. Содержит исходное перечисление 92 тел и предположение, что других нет.
- Виктор А. Залгаллер (1969). Выпуклые многогранники с правильными гранями . Consultants Bureau. ISBN отсутствует. Первое доказательство того, что существует всего 92 тела Джонсона.