Поверхность Ричмонда

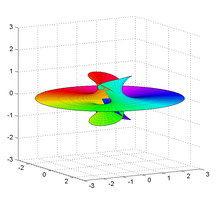
В дифференциальной геометрии поверхность Ричмонда — это минимальная поверхность, впервые описанная Гербертом Уильямом Ричмондом в 1904 году. ^[1] Это семейство поверхностей с одним плоским концом и одним самопересекающимся концом, подобным поверхности Эннепера .

Он имеет параметризацию Вейерштрасса–Эннепера . Это позволяет параметризацию на основе комплексного параметра как${\displaystyle f(z)=1/z^{2},g(z)=z^{m}}$

${\displaystyle {\begin{align}X(z)&=\Re [(-1/2z)-z^{2m+1}/(4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{2m+1}/(4m+2)]\\Z(z)&=\Re [z^{m}/m]\end{align}}}$

Ассоциированное семейство поверхности — это просто поверхность, повернутая вокруг оси z.

Принимая m  = 2, действительное параметрическое выражение принимает вид: ^[2]

${\displaystyle {\begin{aligned}X(u,v)&=(1/3)u^{3}-uv^{2}+{\frac {u}{u^{2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3} - {\frac {v}{u^{2}+v^{2}}}\\Z(u,v)&=2u\end{aligned}}}$

• Эрхан Гюлер и Омер Киши, Richmond Minimal Yüzeyler Ailesi ve Cebirsel Yüzeyleri
• Эрхан Гюлер и Омер Киши, Алгебраические минимальные поверхности (ζ−m, ζm)-типа в трехмерном евклидовом пространстве