Семейство гексагональных кристаллов
| Кристаллическая система | Треугольный | Шестиугольный | |
|---|---|---|---|
| Решетчатая система |  Ромбоэдрический |  Шестиугольный | |
| Пример | .jpg/440px-Dolomite_sur_mimétite_(Maroc).jpg) Доломит (белый) |  α- Кварц |  Берилл |
В кристаллографии гексагональное кристаллическое семейство является одним из шести кристаллических семейств , которое включает две кристаллические системы (гексагональную и тригональную ) и две системы решёток (гексагональную и ромбоэдрическую ). Хотя их часто путают, тригональная кристаллическая система и ромбоэдрическая система решётки не эквивалентны (см. раздел кристаллические системы ниже). [1] В частности, существуют кристаллы, которые имеют тригональную симметрию, но принадлежат к гексагональной решётке (например, α- кварц ).
Семейство гексагональных кристаллов состоит из 12 точечных групп, таких, что по крайней мере одна из их пространственных групп имеет гексагональную решетку в качестве базовой решетки и является объединением гексагональной кристаллической системы и тригональной кристаллической системы. [2] С ней связано 52 пространственных группы, которые являются как раз теми, чья решетка Браве является либо гексагональной, либо ромбоэдрической.
Решетчатые системы
Семейство гексагональных кристаллов состоит из двух систем решеток : гексагональной и ромбоэдрической. Каждая система решеток состоит из одной решетки Браве .

| решетка Бравэ | Шестиугольный | Ромбоэдрический |
|---|---|---|
| символ Пирсона | лс | чР |
| Гексагональная элементарная ячейка |  | 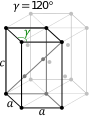 |
| Ромбоэдрическая элементарная ячейка |  | 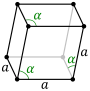 |
В гексагональном семействе кристалл традиционно описывается элементарной ячейкой в виде прямой ромбической призмы с двумя равными осями ( a на a ), прилежащим углом 120° ( γ ) и высотой ( c , которая может отличаться от a ), перпендикулярной двум базовым осям.
Гексагональная элементарная ячейка для ромбоэдрической решетки Браве — это R-центрированная ячейка, состоящая из двух дополнительных точек решетки, которые занимают одну телесную диагональ элементарной ячейки. Есть два способа сделать это, которые можно рассматривать как две нотации, представляющие одну и ту же структуру. В обычной так называемой лицевой настройке дополнительные точки решетки находятся в координатах ( 2 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 3 ) и ( 1 ⁄ 3 , 2 ⁄ 3 , 2 ⁄ 3 ), тогда как в альтернативной обратной настройке они находятся в координатах ( 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 3 ) и ( 2 ⁄ 3 , 1 ⁄ 3 , 2 ⁄ 3 ). [3] В любом случае на элементарную ячейку приходится всего 3 точки решетки, и решетка не является примитивной.
Решетки Браве в семействе гексагональных кристаллов также можно описать ромбоэдрическими осями. [4] Элементарная ячейка — ромбоэдр (что и дало название ромбоэдрической решетке). Это элементарная ячейка с параметрами a = b = c ; α = β = γ ≠ 90°. [5] На практике чаще используется гексагональное описание, поскольку в нем проще работать с системой координат с двумя углами по 90°. Однако в учебниках часто показывают ромбоэдрические оси (для ромбоэдрической решетки), поскольку эта ячейка раскрывает симметрию 3 m кристаллической решетки.
Ромбоэдрическая элементарная ячейка для гексагональной решетки Браве — это D-центрированная [1] ячейка, состоящая из двух дополнительных узлов решетки, которые занимают одну пространственную диагональ элементарной ячейки с координатами ( 1 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 3 ) и ( 2 ⁄ 3 , 2 ⁄ 3 , 2 ⁄ 3 ). Однако такое описание используется редко.
Кристаллические системы
| Кристаллическая система | Требуемые симметрии точечной группы | Точечные группы | Космические группы | Решетки Браве | Решетчатая система |
|---|---|---|---|---|---|
| Треугольный | 1 тройная ось вращения | 5 | 7 | 1 | Ромбоэдрический |
| 18 | 1 | Шестиугольный | |||
| Шестиугольный | 1 шестеричная ось вращения | 7 | 27 |
Семейство гексагональных кристаллов состоит из двух кристаллических систем : тригональной и гексагональной. Кристаллическая система — это набор точечных групп , в котором сами точечные группы и соответствующие им пространственные группы назначены решеточной системе (см. таблицу в разделе Кристаллическая система#Классы кристаллов ).
Тригональная кристаллическая система состоит из 5 точечных групп, имеющих одну тройную ось вращения, которая включает пространственные группы 143–167. Эти 5 точечных групп имеют 7 соответствующих пространственных групп (обозначаемых как R), назначенных ромбоэдрической системе решетки, и 18 соответствующих пространственных групп (обозначаемых как P), назначенных гексагональной системе решетки. Таким образом, тригональная кристаллическая система является единственной кристаллической системой, точечные группы которой имеют более одной системы решетки, связанной с их пространственными группами.
Гексагональная кристаллическая система состоит из 7 точечных групп, имеющих одну ось вращения шестого порядка. Эти 7 точечных групп имеют 27 пространственных групп (от 168 до 194), все из которых относятся к гексагональной решеточной системе.
Тригональная кристаллическая система
Ниже перечислены 5 точечных групп в этой кристаллической системе с их международными номерами и обозначениями, их пространственными группами в названиях и примерами кристаллов. [6] [7] [8]
| Космическая группа № | Группа точек | Тип | Примеры | Космические группы | |||||
|---|---|---|---|---|---|---|---|---|---|
| Имя [1] | Международный | Шён. | Шар. | Кокс. | Шестиугольный | Ромбоэдрический | |||
| 143–146 | Треугольно-пирамидальный | 3 | С 3 | 33 | [3] + | энантиоморфный полярный | карлинит, ярозит | П3, П3 1 , П3 2 | Р3 |
| 147–148 | Ромбоэдрический | 3 | С 3и (С 6 ) | 3× | [2 + ,6 + ] | центросимметричный | доломит , ильменит | П 3 | Р 3 |
| 149–155 | Треугольный трапециевидный | 32 | Д 3 | 223 | [2,3] + | энантиоморфный | абхурит , альфа- кварц (152, 154), киноварь | П312, П321, П3 1 12, П3 1 21, П3 2 12, П3 2 21 | Р32 |
| 156–161 | Дитригонально- пирамидальный | 3м | С 3в | *33 | [3] | полярный | шерл , церит , турмалин , алунит , танталат лития | П3м1, П31м, П3с1, П31с | Р3м, Р3с |
| 162–167 | Дитригональный скаленоэдрический | 3 м | Д 3д | 2*3 | [2 + ,6] | центросимметричный | сурьма , гематит , корунд , кальцит , висмут | П 3 1м, П 3 1ц, П 3 м1, П 3 с1 | Р 3 м, Р 3 с |
Гексагональная кристаллическая система
Ниже перечислены 7 точечных групп ( кристаллических классов ) в этой кристаллической системе, за которыми следуют их представления в системе Германа-Могена или международной системе обозначений и системе обозначений Шёнфлиса , а также примеры минералов , если они существуют. [2] [9]
| Космическая группа № | Группа точек | Тип | Примеры | Космические группы | ||||
|---|---|---|---|---|---|---|---|---|
| Имя [1] | Международный | Шён. | Шар. | Кокс. | ||||
| 168–173 | Шестиугольный пирамидальный | 6 | С 6 | 66 | [6] + | энантиоморфный полярный | нефелин , канкринит | П6, П6 1 , П6 5 , П6 2 , П6 4 , П6 3 |
| 174 | Тригонально-дипирамидальный | 6 | С 3ч | 3* | [2,3 + ] | цезанит , лаурелит | П 6 | |
| 175–176 | Гексагональная дипирамидальная | 6/м | С 6ч | 6* | [2,6 + ] | центросимметричный | апатит , ванадинит | П6/м, П6 3 /м |
| 177–182 | Шестиугольный трапециевидный | 622 | Д 6 | 226 | [2,6] + | энантиоморфный | кальсилит , бета- кварц | П622, П6 1 22, П6 5 22, П6 2 22, П6 4 22, П6 3 22 |
| 183–186 | Дигексагональная пирамидальная | 6мм | С 6в | *66 | [6] | полярный | Гринокит , вюрцит [10] | P6mm, P6cc, P6 3 см, P6 3 мс |
| 187–190 | Дитригонально-дипирамидальный | 6 м2 | Д 3ч | *223 | [2,3] | бенитоит | П 6 м2, П 6 с2, П 6 2м, П 6 2с | |
| 191–194 | Дигексагональная дипирамидальная | 6/ммм | Д 6ч | *226 | [2,6] | центросимметричный | берилл | P6/mmm, P6/mcc, P6 3 /mcm, P6 3 /mmc |
Объем элементарной ячейки определяется как 2 c • sin(60°)
Гексагональная плотноупакованная

Гексагональная плотноупакованная (ГПУ) — один из двух простых типов атомной упаковки с самой высокой плотностью, другой — гранецентрированная кубическая (ГЦК). Однако, в отличие от ГЦК, это не решетка Бравэ, поскольку есть два неэквивалентных набора точек решетки. Вместо этого ее можно построить из гексагональной решетки Бравэ, используя двухатомный мотив (дополнительный атом примерно в ( 2 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 2 )), связанный с каждой точкой решетки. [11]
Многоэлементные конструкции
Соединения, состоящие из более чем одного элемента (например, бинарные соединения ), часто имеют кристаллические структуры, основанные на гексагональном кристаллическом семействе. Некоторые из наиболее распространенных перечислены здесь. Эти структуры можно рассматривать как две или более взаимопроникающих подрешеток, где каждая подрешетка занимает интерстициальные позиции других.
Структура вюрцита



Кристаллическая структура вюрцита обозначается обозначением Strukturbericht B4 и символом Пирсона hP4. Соответствующая пространственная группа — № 186 (в классификации Международного союза кристаллографии) или P6 3 mc (в нотации Германна-Могена ). Символы Германна-Могена в P6 3 mc можно прочитать следующим образом: [13]
- 6 3 .. : шестикратное вращение винта вокруг оси c
- .m. : плоскость зеркала с нормалью {100}
- ..c : плоскость скольжения в c -направлениях с нормалью {120}.
Среди соединений, которые могут иметь структуру вюрцита, есть сам вюрцит ( ZnS с содержанием железа вместо цинка до 8% ), иодид серебра (AgI), оксид цинка (ZnO), сульфид кадмия (CdS), селенид кадмия (CdSe), карбид кремния (α-SiC), нитрид галлия (GaN), нитрид алюминия (AlN), нитрид бора (w-BN) и другие полупроводники . [14] В большинстве этих соединений вюрцит не является предпочтительной формой объемного кристалла, но структура может быть предпочтительной в некоторых нанокристаллических формах материала.
В материалах с более чем одной кристаллической структурой к эмпирической формуле иногда добавляют префикс «w-», чтобы обозначить кристаллическую структуру вюрцита, например, w-BN .
Каждый из двух отдельных типов атомов образует подрешетку, которая является гексагональной плотноупакованной (тип HCP). Если рассматривать все вместе, то атомные позиции такие же, как в лонсдейлите (гексагональный алмаз ). Каждый атом тетраэдрически координирован. Структуру также можно описать как решетку HCP цинка с атомами серы, занимающими половину тетраэдрических пустот , или наоборот.
Структура вюрцита нецентросимметрична (т.е. не имеет инверсионной симметрии ). Благодаря этому кристаллы вюрцита могут (и обычно имеют) обладать такими свойствами, как пьезоэлектричество и пироэлектричество , которые отсутствуют у центросимметричных кристаллов. [ необходима цитата ]
Структура арсенида никеля
Структура арсенида никеля состоит из двух взаимопроникающих подрешеток: примитивной гексагональной подрешетки никеля и гексагональной плотноупакованной подрешетки мышьяка. Каждый атом никеля октаэдрически координирован с шестью атомами мышьяка, в то время как каждый атом мышьяка тригонально призматически координирован с шестью атомами никеля. [15] Структуру также можно описать как решетку HCP мышьяка с никелем, занимающим каждую октаэдрическую пустоту .
Соединения, имеющие структуру NiAs, обычно представляют собой халькогениды , арсениды , антимониды и висмутиды переходных металлов . [ требуется ссылка ]
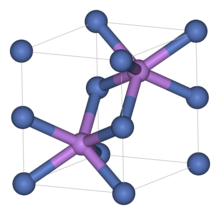
Ниже перечислены члены группы никеля: [16]
- Ачавалит : FeSe
- Брейтгауптит : NiSb
- Фреболдит: CoSe
- Котульскит: Pd(Te,Bi)
- Лангистит: (Co,Ni)As
- Никелин: NiAs
- Соболевскит: Pd(Bi,Te)
- Садбериит: (Pd,Ni)Sb
В двух измерениях
Существует только одна гексагональная решетка Браве в двух измерениях: гексагональная решетка.
| решетка Бравэ | Шестиугольный |
|---|---|
| символ Пирсона | л.с. |
| Элементарная ячейка |  |
Смотрите также
Ссылки
- ^ abcd Hahn, Theo, ed. (2005). Международные таблицы по кристаллографии (5-е изд.). Дордрехт, Нидерланды: Опубликовано для Международного союза кристаллографии издательством Springer. ISBN 978-0-7923-6590-7.
- ^ ab Dana, James Dwight; Hurlbut, Cornelius Searle (1959). Dana's Manual of Mineralogy (17-е изд.). Нью-Йорк: Chapman Hall. С. 78–89.
- ^ Эдвард Принс (2004). Математические методы в кристаллографии и материаловедении . Springer Science & Business Media. стр. 41.
- ^ "Диаграммы и таблицы пространственных групп среднего разрешения". img.chem.ucl.ac.uk .
- ^ Эшкрофт, Нил В.; Мермин, Н. Дэвид (1976). Физика твердого тела (1-е изд.). Холт, Райнхарт и Уинстон. стр. 119. ISBN 0-03-083993-9.
- ^ Pough, Frederick H.; Peterson, Roger Tory (1998). Полевое руководство по горным породам и минералам. Houghton Mifflin Harcourt. стр. 62. ISBN 0-395-91096-X.
- ^ Херлбат, Корнелиус С.; Кляйн, Корнелис (1985). Руководство по минералогии (20-е изд.). Wiley. стр. 78–89. ISBN 0-471-80580-7.
- ^ «Кристаллография и минералы, упорядоченные по форме кристаллов». Webmineral .
- ^ "Кристаллография". Webmineral.com . Получено 2014-08-03 .
- ^ "Минералы в гексагональной кристаллической системе, класс дигексагональной пирамиды (6 мм)". Mindat.org . Получено 2014-08-03 .
- ^ Джасвон, Морис Аарон (1965-01-01). Введение в математическую кристаллографию. American Elsevier Pub. Co.
- ^ Де Граф, Марк; МакГенри, Майкл Э. (2012). Структура материалов; Введение в кристаллографию, дифракцию и симметрию (PDF) . Cambridge University Press. стр. 16.
- ^ Хичкок, Питер Б. (1988). Международные таблицы по кристаллографии, том А.
- ^ Того, Ацуши; Чапут, Лоран; Танака, Исао (2015-03-20). "Распределения времен жизни фононов в зонах Бриллюэна". Physical Review B. 91 ( 9): 094306. arXiv : 1501.00691 . Bibcode : 2015PhRvB..91i4306T. doi : 10.1103/PhysRevB.91.094306. S2CID 118851924.
- ^ Неорганическая химия Дьюарда Шрайвера и Питера Аткинса, 3-е издание, WH Freeman and Company, 1999, стр. 47,48.
- ^ http://www.mindat.org/min-2901.html Mindat.org
