Октадекагон

Правильный октадекагон
Правильный октадекагон
	Правильный октадекагон
Тип	Правильный многоугольник
Ребра и вершины	18
Символ Шлефли	{18}, т{9}
Диаграммы Кокстера–Дынкина	;
Группа симметрии	Двугранный (D 18 ), порядок 2×18
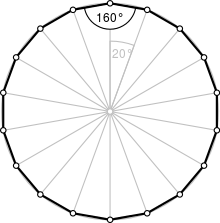
Внутренний угол ( градусы )	160°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

Многоугольник с 18 гранями

В геометрии октадекагон (или октакаидекагон ^[1]) или 18-угольник — это восемнадцатиугольник . ^[2]

Правильный октадекагон

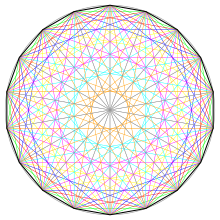
Правильный октадекагон имеет символ Шлефли {18} и может быть построен как квазиправильный усеченный девятиугольник , t{9}, который чередует два типа ребер.

Строительство

Так как 18 = 2 × 3 ² , то правильный октадекагон нельзя построить с помощью циркуля и линейки . ^[3] Однако его можно построить с помощью невзиса или трисекции угла с помощью томагавка .

Октадекагон, точное построение на основе трисекции угла 120° с помощью томагавка, анимация 1 мин 34 с.

Следующая приблизительная конструкция очень похожа на конструкцию девятиугольника, поскольку октадекагон может быть построен как усеченный девятиугольник. Это также осуществимо с использованием исключительно циркуля и линейки.

Уменьшите угол AMC (также 60°) с помощью четырех биссектрис и постройте треть дуги окружности MON с приближенным решением между биссектрисами угла w ₃ и w ₄ . Прямая вспомогательная линия g направлена через точку O к точке N (фактически линейка в точках O и N), между O и N, поэтому вспомогательной линии нет. Таким образом, дуга окружности MON свободно доступна для последующей точки пересечения R. $\scriptstyle \angle {}$ АМР = 19,999999994755615...° 360° ÷ 18 = 20° $\scriptstyle \angle {}$ АМР - 20° = -5,244...E-9° Пример, иллюстрирующий ошибку : При радиусе описанной окружности r = 100 000 км абсолютная погрешность первой стороны составит приблизительно -9 мм. См. также расчет наноган (Berechnung, немецкий) 6.0 JMR эквивалентен AMR. $\scriptstyle \angle {}$ $\scriptstyle \angle {}$

Симметрия

Правильный октадекагон имеет симметрию Dih ₁₈ , порядок 36. Существует 5 диэдральных симметрий подгрупп: Dih ₉ , (Dih ₆ , Dih ₃ ) и (Dih ₂ Dih ₁ ), а также 6 симметрий циклических групп : (Z ₁₈ , Z ₉ ), (Z ₆ , Z ₃ ) и (Z ₂ , Z ₁ ).

Эти 15 симметрий можно увидеть в 12 различных симметриях на октадекагоне. Джон Конвей помечает их буквой и порядком группы. ^[4] Полная симметрия правильной формы — r36 , и ни одна симметрия не помечена как a1 . Диэдральные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце помечены как g для их центральных порядков инерции.

Каждая подгруппа симметрии допускает одну или несколько степеней свободы для нерегулярных форм. Только подгруппа g18 не имеет степеней свободы, но может рассматриваться как направленные ребра .

Вскрытие

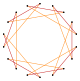
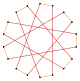
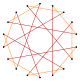
Коксетер утверждает, что каждый зоногон (2 m -угольник, противоположные стороны которого параллельны и имеют одинаковую длину) можно разрезать на m ( m -1)/2 параллелограммов. ^[6] В частности, это верно для правильных многоугольников с равным числом сторон, в этом случае все параллелограммы являются ромбами. Для правильного октадекагона m = 9 , и его можно разделить на 36: 4 набора по 9 ромбов. Это разложение основано на проекции многоугольника Петри 9-куба с 36 из 4608 граней. Список OEIS : A006245 перечисляет количество решений как 112018190, включая до 18-кратных вращений и хиральных форм в отражении.

Разрезание на 36 ромбов

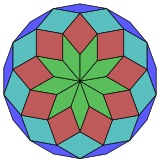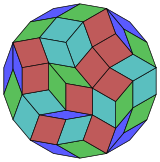Использует

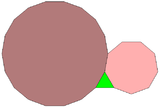
Правильный треугольник, девятиугольник и октадекагон могут полностью окружить точку на плоскости, одну из 17 различных комбинаций правильных многоугольников с этим свойством. ^[7] Однако этот шаблон не может быть распространен на архимедову мозаику плоскости: поскольку треугольник и девятиугольник оба имеют нечетное число сторон, ни один из них не может быть полностью окружен кольцом, чередующим два других вида многоугольников.

Правильный октадекагон может замостить плоскость вогнутыми шестиугольными зазорами. А другая мозаика смешивает девятиугольники и восьмиугольные зазоры. Первая мозаика связана с усеченной шестиугольной мозаикой , а вторая — с усеченной тришестиугольной мозаикой .

Связанные цифры

Октадекаграмма — это 18-сторонний звездчатый многоугольник, представленный символом {18/n}. Существует два правильных звездчатых многоугольника : {18/5} и {18/7}, использующие те же точки, но соединяющие каждую пятую или седьмую точку. Существует также пять соединений: {18/2} сокращается до 2{9} или двух девятиугольников , {18/3} сокращается до 3{6} или трех шестиугольников , {18/4} и {18/8} сокращаются до 2{9/2} и 2{9/4} или двух эннеаграмм , {18/6} сокращается до 6{3} или 6 равносторонних треугольников, и, наконец, {18/9} сокращается до 9{2} как девять двуугольников .

Соединения и звездчатые многоугольники
н	1	2	3	4	5	6	7	8	9
Форма	Выпуклый многоугольник	Соединения			Звездный многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{18/1} = {18}	{18/2} = 2{9}	{18/3} = 3{6}	{18/4} = 2{9/2}	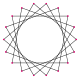{18/5}	{18/6} = 6{3}	{18/7}	{18/8} = 2{9/4}	{18/9} = 9{2}
Внутренний угол	160°	140°	120°	100°	80°	60°	40°	20°	0°

Более глубокие усечения правильного эннеагона и эннеаграмм могут производить изогональные ( вершинно-транзитивные ) промежуточные формы октадекаграмм с равноотстоящими вершинами и двумя длинами ребер. Другие усечения образуют двойные покрытия: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9}. ^[8]

Вершинно-транзитивные усечения эннеагона и эннеаграмм
Квазирегулярный	изогональный	Квазирегулярное двойное покрытие
т{9}={18}		т{9/8}={18/8} =2{9/4}
т{9/5}={18/5}		т{9/4}={18/4} =2{9/2}
т{9/7}={18/7}		т{9/2}={18/2} =2{9}

Петри полигоны

Правильный косой октадекагон является многоугольником Петри для ряда многогранников более высокой размерности, показанных на этих косых ортогональных проекциях из плоскостей Коксетера :

Восьмидесятиугольные полигоны Петри
А ₁₇	Б ₉		Д ₁₀		Е ₇
17-симплекс	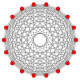9-ортоплекс	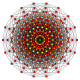9-кубовый	7 ₁₁	1 ₇₁	3 ₂₁	2 ₃₁	1 ₃₂

Ссылки

^ Кинси, Л. Кристин ; Мур, Тереза Э. (2002), Симметрия, форма и поверхности: введение в математику через геометрию, Springer, стр. 86, ISBN 9781930190092.
^ Адамс, Генри (1907), Справочник инженера Касселла: Содержит факты и формулы, принципы и практику, во Всех отраслях машиностроения, Д. Маккей, стр. 528.
^ Конвей, Джон Б. (2010), Математические связи: курс обучения, Американское математическое общество, стр. 31, ISBN 9780821849798.
^ Джон Х. Конвей, Хайди Бергиль, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
^ Хиршхорн и Хант 1985.
^ Коксетер , Математические развлечения и эссе, тринадцатое издание, стр. 141
^ Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. д., Джон У. Паркер и сын, стр. 134.
^ Более светлая сторона математики: Труды конференции памяти Эжена Стренса по занимательной математике и ее истории, (1994), Метаморфозы многоугольников , Бранко Грюнбаум

Хиршхорн, MD; Хант, DC (1985), «Равносторонние выпуклые пятиугольники, которые заполняют плоскость» (PDF) , Журнал комбинаторной теории, Серия A , 39 (1): 1– 18, doi : 10.1016/0097-3165(85)90078-0 , ISSN 1096-0899, MR 0787713 , получено 30 октября 2020 г.
октадекагон

Внешние ссылки

Вайсштейн, Эрик В. «Октадекагон». MathWorld .

[1] Кинси, Л. Кристин ; Мур, Тереза Э. (2002), Симметрия, форма и поверхности: введение в математику через геометрию, Springer, стр. 86, ISBN 9781930190092.

[2] Адамс, Генри (1907), Справочник инженера Касселла: Содержит факты и формулы, принципы и практику, во Всех отраслях машиностроения, Д. Маккей, стр. 528.

[3] Конвей, Джон Б. (2010), Математические связи: курс обучения, Американское математическое общество, стр. 31, ISBN 9780821849798.

[4] Джон Х. Конвей, Хайди Бергиль, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)

[FOOTNOTEHirschhornHunt1985-5] Хиршхорн и Хант 1985.

[6] Коксетер , Математические развлечения и эссе, тринадцатое издание, стр. 141

[7] Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. д., Джон У. Паркер и сын, стр. 134.

[8] Более светлая сторона математики: Труды конференции памяти Эжена Стренса по занимательной математике и ее истории, (1994), Метаморфозы многоугольников , Бранко Грюнбаум