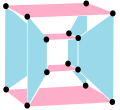
Правильный сложный многоугольник

Три вида правильного комплексного многоугольника ₄ {4} ₂ ,

Этот сложный многоугольник имеет 8 ребер (комплексных линий), обозначенных как a .. h , и 16 вершин. Четыре вершины лежат на каждом ребре, и два ребра пересекаются в каждой вершине. На левом изображении обведенные квадраты не являются элементами многогранника, а включены просто для того, чтобы помочь идентифицировать вершины, лежащие на одной и той же комплексной линии. Восьмиугольный периметр левого изображения не является элементом многогранника, но является многоугольником Петри . [1] На среднем изображении каждое ребро представлено как действительная линия, и четыре вершины в каждой линии можно увидеть более четко.

Перспективный эскиз, представляющий 16 вершинных точек как большие черные точки и 8 4-ребер как ограниченные квадраты внутри каждого ребра. Зеленый путь представляет восьмиугольный периметр левого изображения.

В геометрии правильный комплексный многоугольник является обобщением правильного многоугольника в реальном пространстве до аналогичной структуры в комплексном гильбертовом пространстве , где каждое действительное измерение сопровождается мнимым . Правильный многоугольник существует в 2 действительных измерениях, , в то время как комплексный многоугольник существует в двух комплексных измерениях, , которым можно дать действительные представления в 4 измерениях, , которые затем должны быть спроецированы до 2 или 3 действительных измерений для визуализации. Комплексный многоугольник обобщается как комплексный многогранник в .${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbb {C} ^{2}}$${\displaystyle \mathbb {R} ^{4}}$${\displaystyle \mathbb {C} ^{n}}$

Сложный многоугольник можно понимать как совокупность сложных точек, линий, плоскостей и т. д., где каждая точка является пересечением нескольких линий, каждая линия — нескольких плоскостей и т. д.

Правильные сложные многоугольники полностью охарактеризованы и могут быть описаны с помощью символической нотации, разработанной Коксетером .

Правильный сложный многоугольник со всеми 2-ребрами может быть представлен графом , тогда как формы с k -ребрами могут быть связаны только гиперграфами . K -ребро можно рассматривать как набор вершин, без подразумеваемого порядка. Их можно нарисовать с попарными 2-ребрами, но это не является структурно точным.

В то время как 1-многогранники могут иметь неограниченное число p , конечные правильные комплексные многоугольники, за исключением многоугольников двойной призмы _p {4} ₂ , ограничены элементами с 5 ребрами (пятиугольными ребрами), а бесконечные правильные апейрогоны также включают элементы с 6 ребрами (шестиугольными ребрами).

Шепард изначально разработал модифицированную форму обозначения Шлефли для правильных многогранников. Для многоугольника, ограниченного p ₁ -ребрами, с p ₂ -множеством в качестве вершинной фигуры и общей группой симметрии порядка g , мы обозначаем многоугольник как p ₁ ( g ) p ₂ .

Тогда число вершин V _равно g / p2 _, а число ребер E равно g / p1 .

Сложный многоугольник, показанный выше, имеет восемь квадратных ребер ( p ₁ =4) и шестнадцать вершин ( p ₂ =2). Из этого мы можем вывести, что g = 32, что дает модифицированный символ Шлефли 4(32)2.

Более современная нотация _{p 1} { q } _{p 2} принадлежит Кокстеру [ 2 ^] и основана на теории групп. Как группа симметрии, ее символ — _{p 1} [ q ] _{p 2} .

Группа симметрии _{p 1} [ q ] _{p 2} представлена ​​2 генераторами R ₁ , R ₂ , где: R ₁ ^{p ₁} = R ₂ ^{p ₂} = I. Если q четное, (R ₂ R ₁ ) ^{q /2} = (R ₁ R ₂ ) ^{q /2} . Если q нечетное, (R ₂ R ₁ ) ^{( q −1)/2} R ₂ = (R ₁ R ₂ ) ^{( q −1)/2} R ₁ . Когда q нечетное, p ₁ = p ₂ .

Для ₄ [4] ₂ имеет R ₁ ⁴ = R ₂ ² = I, (R ₂ R ₁ ) ² = (R ₁ R ₂ ) ² .

Для ₃ [5] ₃ имеет R ₁ ³ = R ₂ ³ = I, (R ₂ R ₁ ) ² R ₂ = (R ₁ R ₂ ) ² R ₁ .

Коксетер также обобщил использование диаграмм Коксетера–Дынкина на комплексные многогранники, например, комплексный многоугольник _p { q } _r представлен каки эквивалентная группа симметрии, _p [ q ] _r , является диаграммой без колец. Узлы p и r представляют зеркала, создающие p и r изображения на плоскости. Непомеченные узлы на диаграмме имеют неявные 2 метки. Например, действительный правильный многоугольник — это ₂ { q } ₂ или { q } или.

Одно ограничение: узлы, соединенные нечетными порядками ветвей, должны иметь идентичные порядки узлов. Если нет, группа создаст «звездчатые» полигоны с перекрывающимися элементами. Такиявляются обычными, в то время какзвездный.

12 неприводимых групп Шепарда с их индексными соотношениями подгрупп. [3]	Подгруппы из <5,3,2> 30 , <4,3,2> 12 и <3,3,2> 6
Подгруппы связаны путем удаления одного отражения: p [2 q ] 2 --> p [ q ] p , индекс 2 и p [4] q --> p [ q ] p , индекс q .

Коксетер перечислил этот список правильных комплексных многоугольников в . Правильный комплексный многоугольник, _p { q } _r или${\displaystyle \mathbb {C} ^{2}}$, имеет p -рёбер и r -угольные вершинные фигуры . _p { q } _r является конечным многогранником, если ( p  +  r ) q  >  pr ( q  − 2).

Ее симметрия записывается как _p [ q ] _r , называется группой Шепарда , аналогичной группе Кокстера , но также допускающей унитарные отражения .

Для незвездных групп порядок группы _p [ q ] _r можно вычислить как . ^[4]${\displaystyle g=8/q\cdot (1/p+2/q+1/r-1)^{-2}}$

Число Кокстера для _p [ q ] _r равно , поэтому порядок группы также может быть вычислен как . Правильный комплексный многоугольник можно нарисовать в ортогональной проекции с h -угольной симметрией.${\displaystyle h=2/(1/p+2/q+1/r-1)}$${\displaystyle g=2h^{2}/q}$

Решения ранга 2, генерирующие сложные многоугольники:

Группа	G3 = G( q ,1,1)	G 2 = G( п ,1,2)	Г 4	Г 6	Г 5	Г 8	Г 14	Г 9	Г 10	Г 20	Г 16	Г 21	Г 17	Г 18
	2 [ q ] 2 , q = 3,4...	р [4] 2 , р = 2,3...	3 [3] 3	3 [6] 2	3 [4] 3	4 [3] 4	3 [8] 2	4 [6] 2	4 [4] 3	3 [5] 3	5 [3] 5	3 [10] 2	5 [6] 2	5 [4] 3
Заказ	2 кв.	2 п 2	24	48	72	96	144	192	288	360	600	720	1200	1800
час	д	2 стр.	6	12			24			30		60

Исключенные решения с нечетным q и неравными p и r : ₆ [3] ₂ , ₆ [3] ₃ , ₉ [3] ₃ , ₁₂ [3] ₃ , ..., ₅ [5] ₂ , ₆ [5] ₂ , ₈ [5] ₂ , ₉ [5] ₂ , ₄ [7] ₂ , ₉ [5] ₂ , ₃ [9] ₂ и ₃ [11] ₂ .

Другие целые q с неравными p и r создают звездные группы с перекрывающимися фундаментальными областями:,,,,, и.

Двойственный многоугольник _p { q } _r есть _r { q } _p . Многоугольник вида _p { q } _p является самодвойственным. Группы вида _p [2 q ] ₂ имеют половинную симметрию _p [ q ] _p , поэтому правильный многоугольникто же самое, что и квазирегулярный. Также, правильный многоугольник с теми же порядками узлов,, имеют альтернативную конструкцию, что позволяет соседним ребрам быть двух разных цветов. ^[5]

Порядок группы g используется для вычисления общего числа вершин и ребер. Он будет иметь g / r вершин и g / p ребер. Когда p = r , число вершин и ребер равно. Это условие требуется, когда q нечетно.

Группа p [ q ] r ,, можно представить двумя матрицами: ^[6]

Имя	Р 1	Р 2
Заказ	п	г
Матрица	${\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\(e^{2\pi i/p}-1)k&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&(e^{2\pi i/r}-1)k\\0&e^{2\pi i/r}\end{smallmatrix}}\right]}$

С

${\displaystyle k={\sqrt {\frac {\cos({\frac {\pi }{p}} - {\frac {\pi }{r}})+\cos({\frac {2\pi }{q}})}{2\sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}}}}}$

Примеры

Имя Р 1 Р 2 Заказ п д Матрица ${\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&e^{2\pi i/q}\\\end{smallmatrix}}\right]}$	Имя Р 1 Р 2 Заказ п 2 Матрица ${\displaystyle \left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]}$	Имя Р 1 Р 2 Заказ 3 3 Матрица ${\displaystyle \left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\{\frac {-3+{\sqrt {3}}i}{2}}&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1&{\frac {-3+{\sqrt {3}}i}{2}}\\0&{\frac {-1+{\sqrt {3}}i}{2}}\\\end{smallmatrix}}\right]}$
Имя Р 1 Р 2 Заказ 4 4 Матрица ${\displaystyle \left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&i\\\end{smallmatrix}}\right]}$	Имя Р 1 Р 2 Заказ 4 2 Матрица ${\displaystyle \left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]}$	Имя Р 1 Р 2 Заказ 3 2 Матрица ${\displaystyle \left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\{\frac {-3+{\sqrt {3}}i}{2}}&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1&-2\\0&-1\\\end{smallmatrix}}\right]}$

Коксетер перечислил комплексные многоугольники в Таблице III Правильных комплексных многогранников. ^[7]

Группа	Заказ	Число Кокстера	Полигон		Вершины	Края		Примечания
G ( q , q ,2) 2 [ q ] 2 = [ q ] q = 2,3,4,...	2 кв.	д	2 { д } 2		д	д	{}	Действительные правильные многоугольники То же, что и То же самое, что иесли q четное

Группа	Заказ	Число Кокстера	Полигон			Вершины	Края		Примечания
G( п ,1,2) п [4] 2 п=2,3,4,...	2 п 2	2 стр.	п (2 п 2 )2	п {4} 2		стр 2	2 стр.	п {}	то же самое, что p {}× p {} или ${\displaystyle \mathbb {R} ^{4}}$представление в виде p - p дуопризмы
			2(2 п 2 ) п	2 {4} п		2 стр.	стр 2	{}	${\displaystyle \mathbb {R} ^{4}}$представление в виде p - p дуопирамиды
Г(2,1,2) 2 [4] 2 = [4]	8	4		2 {4} 2 = {4}		4	4	{}	то же, что {}×{} или Действительный квадрат
Г(3,1,2) 3 [4] 2	18	6	6(18)2	3 {4} 2		9	6	3 {}	то же самое, что 3 {}× 3 {} или ${\displaystyle \mathbb {R} ^{4}}$представление в виде 3-3 дуопризмы
			2(18)3	2 {4} 3		6	9	{}	${\displaystyle \mathbb {R} ^{4}}$представление в виде 3-3 дуопирамиды
Г(4,1,2) 4 [4] 2	32	8	8(32)2	4 {4} 2		16	8	4 {}	то же самое, что 4 {}× 4 {} или ${\displaystyle \mathbb {R} ^{4}}$представление в виде 4-4 дуопризмы или {4,3,3}
			2(32)4	2 {4} 4		8	16	{}	${\displaystyle \mathbb {R} ^{4}}$представление в виде 4-4 дуопирамиды или {3,3,4}
Г(5,1,2) 5 [4] 2	50	25	5(50)2	5 {4} 2		25	10	5 {}	то же самое, что 5 {}× 5 {} или ${\displaystyle \mathbb {R} ^{4}}$представление в виде 5-5 дуопризмы
			2(50)5	2 {4} 5		10	25	{}	${\displaystyle \mathbb {R} ^{4}}$представление в виде 5-5 дуопирамиды
Г(6,1,2) 6 [4] 2	72	36	6(72)2	6 {4} 2		36	12	6 {}	то же самое, что 6 {}× 6 {} или ${\displaystyle \mathbb {R} ^{4}}$представление в виде 6-6 дуопризмы
			2(72)6	2 {4} 6		12	36	{}	${\displaystyle \mathbb {R} ^{4}}$представление в виде 6-6 дуопирамиды
Г 4 =Г(1,1,2) 3 [3] 3 <2,3,3>	24	6	3(24)3	3 {3} 3		8	8	3 {}	Конфигурация Мёбиуса–Кантора самодвойственная, то же самое, что ${\displaystyle \mathbb {R} ^{4}}$представление как {3,3,4}
Г 6 3 [6] 2	48	12	3(48)2	3 {6} 2		24	16	3 {}	то же самое, что и
				3 {3} 2					звездный многоугольник
			2(48)3	2 {6} 3		16	24	{}
				2 {3} 3					звездный многоугольник
Г 5 3 [4] 3	72	12	3(72)3	3 {4} 3		24	24	3 {}	самодвойственный, то же самое, что ${\displaystyle \mathbb {R} ^{4}}$представление как {3,4,3}
Г 8 4 [3] 4	96	12	4(96)4	4 {3} 4		24	24	4 {}	самодвойственный, то же самое, что ${\displaystyle \mathbb {R} ^{4}}$представление как {3,4,3}
Г 14 3 [8] 2	144	24	3(144)2	3 {8} 2		72	48	3 {}	то же самое, что и
				3 {8/3} 2					звездный многоугольник, то же самое, что
			2(144)3	2 {8} 3		48	72	{}
				2 {8/3} 3					звездный многоугольник
Г 9 4 [6] 2	192	24	4(192)2	4 {6} 2		96	48	4 {}	то же самое, что и
			2(192)4	2 {6} 4		48	96	{}
				4 {3} 2		96	48	{}	звездный многоугольник
				2 {3} 4		48	96	{}	звездный многоугольник
Г 10 4 [4] 3	288	24	4(288)3	4 {4} 3		96	72	4 {}
		12		4 {8/3} 3					звездный многоугольник
		24	3(288)4	3 {4} 4		72	96	3 {}
		12		3 {8/3} 4					звездный многоугольник
Г 20 3 [5] 3	360	30	3(360)3	3 {5} 3		120	120	3 {}	самодвойственный, то же самое, что ${\displaystyle \mathbb {R} ^{4}}$представление как {3,3,5}
				3 {5/2} 3					самодвойственный, звездный многоугольник
Г 16 5 [3] 5	600	30	5(600)5	5 {3} 5		120	120	5 {}	самодвойственный, то же самое, что ${\displaystyle \mathbb {R} ^{4}}$представление как {3,3,5}
		10		5 {5/2} 5					самодвойственный, звездный многоугольник
Г 21 3 [10] 2	720	60	3(720)2	3 {10} 2		360	240	3 {}	то же самое, что и
				3 {5} 2					звездный многоугольник
				3 {10/3} 2					звездный многоугольник, то же самое, что
				3 {5/2} 2					звездный многоугольник
			2(720)3	2 {10} 3		240	360	{}
				2 {5} 3					звездный многоугольник
				2 {10/3} 3					звездный многоугольник
				2 {5/2} 3					звездный многоугольник
Г 17 5 [6] 2	1200	60	5(1200)2	5 {6} 2		600	240	5 {}	то же самое, что и
		20		5 {5} 2					звездный многоугольник
		20		5 {10/3} 2					звездный многоугольник
		60		5 {3} 2					звездный многоугольник
		60	2(1200)5	2 {6} 5		240	600	{}
		20		2 {5} 5					звездный многоугольник
		20		2 {10/3} 5					звездный многоугольник
		60		2 {3} 5					звездный многоугольник
Г 18 5 [4] 3	1800	60	5(1800)3	5 {4} 3		600	360	5 {}
		15		5 {10/3} 3					звездный многоугольник
		30		5 {3} 3					звездный многоугольник
		30		5 {5/2} 3					звездный многоугольник
		60	3(1800)5	3 {4} 5		360	600	3 {}
		15		3 {10/3} 5					звездный многоугольник
		30		3 {3} 5					звездный многоугольник
		30		3 {5/2} 5					звездный многоугольник

Многоугольники вида _p {2 r } _q можно визуализировать с помощью q цветовых наборов p -ребер. Каждое p -ребро рассматривается как правильный многоугольник, при этом граней нет.

Сложные многоугольники ₂ { r } _q

Многоугольники вида ₂ {4} _q называются обобщенными ортоплексами . Они имеют общие вершины с 4D q - q дуопирамидами , вершины которых соединены 2-ребрами.

• 
  ₂ {4} ₂ ,, с 4 вершинами и 4 ребрами
• 
  ₂ {4} ₃ ,, с 6 вершинами и 9 ребрами ^[8]
• 
  ₂ {4} ₄ ,, с 8 вершинами и 16 ребрами
• 
  ₂ {4} ₅ ,, с 10 вершинами и 25 ребрами
• 
  ₂ {4} ₆ ,, с 12 вершинами и 36 ребрами
• 
  ₂ {4} ₇ ,, с 14 вершинами и 49 ребрами
• 
  ₂ {4} ₈ ,, с 16 вершинами и 64 ребрами
• 
  ₂ {4} ₉ ,, с 18 вершинами и 81 ребром
• 
  ₂ {4} ₁₀ ,, с 20 вершинами и 100 ребрами

Сложные многоугольники _p {4} ₂

Многоугольники вида _p {4} ₂ называются обобщенными гиперкубами (квадратами для многоугольников). Они разделяют вершины с 4D p - p дуопризмами , вершины соединены p-ребрами. Вершины нарисованы зеленым цветом, а p -ребра нарисованы альтернативными цветами, красным и синим. Перспектива слегка искажается для нечетных измерений, чтобы переместить перекрывающиеся вершины из центра.

• 
  ₂ {4} ₂ ,или, с 4 вершинами и 4 2-ребрами
• 
  ₃ {4} ₂ ,или, с 9 вершинами и 6 (треугольными) 3-ребрами ^[9]
• 
  ₄ {4} ₂ ,или, с 16 вершинами и 8 (квадратными) 4-ребрами
• 
  ₅ {4} ₂ ,или, с 25 вершинами и 10 (пятиугольными) 5-ребрами
• 
  ₆ {4} ₂ ,или, с 36 вершинами и 12 (шестиугольными) 6-гранниками
• 
  ₇ {4} ₂ ,или, с 49 вершинами и 14 (семиугольными)7-ребрами
• 
  ₈ {4} ₂ ,или, с 64 вершинами и 16 (восьмиугольными) 8-ребрами
• 
  ₉ {4} ₂ ,или, с 81 вершиной и 18 (девятиугольными) 9-ребрами
• 
  ₁₀ {4} ₂ ,или, со 100 вершинами и 20 (десятиугольными) 10-ребрами

Сложные многоугольники _p { r } ₂

• 
  ₃ {6} ₂ ,или, с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребрьев красного и синего цвета ^[10]
• 
  ₃ {8} ₂ ,или, с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора по 3-ребра красного и синего цвета ^[11]

Сложные многоугольники, _p { r } _p

Многоугольники вида _p { r } _p имеют одинаковое количество вершин и ребер. Они также являются самодвойственными.

• 
  ₃ {3} ₃ ,или, с 8 вершинами черного цвета и 8 3-ребрами, окрашенными в 2 набора 3-ребрьев красного и синего цвета ^[12]
• 
  ₃ {4} ₃ ,или, с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор заполнен ^[13]
• 
  ₄ {3} ₄ ,или, с 24 вершинами и 24 4-ребрами, показанными в 4 наборах цветов ^[14]
• 
  ₃ {5} ₃ ,или, со 120 вершинами и 120 3-ребрами ^[15]
• 
  ₅ {3} ₅ ,или, со 120 вершинами и 120 5-ребрами ^[16]

Трехмерные перспективные проекции сложных многоугольников _p {4} ₂ могут отображать структуру точек и ребер сложного многоугольника, при этом масштаб не сохраняется.

Дуалы ₂ {4} _p : можно увидеть, добавив вершины внутрь ребер и добавив ребра вместо вершин.

• 
  ₂ {4} ₃ ,с 6 вершинами, 9 ребрами в 3 наборах
• 
  ₃ {4} ₂ ,с 9 вершинами, 6 3-ребрами в 2 наборах цветов, как
• 
  ₄ {4} ₂ ,с 16 вершинами, 8 4-гранниками в 2 наборах цветов и заполненным квадратом с 4-гранниками, как
• 
  ₅ {4} ₂ ,с 25 вершинами, 10 5-ребрами в 2 наборах цветов, как

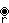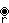Квазиправильный многоугольник — это усечение правильного многоугольника. Квазиправильный многоугольниксодержит альтернативные ребра правильных многоугольниковиКвазиправильный многоугольник имеет p вершин на p-ребрах правильной формы.

Примеры квазиправильных многоугольников

п [ д ] р	2 [4] 2	3 [4] 2	4 [4] 2	5 [4] 2	6 [4] 2	7 [4] 2	8 [4] 2	3 [3] 3	3 [4] 3
Обычный	4 2-реберных	9 3-ребер	16 4-реберных	25 5-гранный	36 6-гранный	49 7-гранный	64 8-гранные
Квазирегулярный	= 4+4 2-реберные	6 2-ребер 9 3-ребер	8 2-реберных 16 4-реберных	10 2-реберных 25 5-реберных	12 2-реберных 36 6-реберных	14 2-ребер 49 7-ребер	16 2-ребер 64 8-ребер	=	=
Обычный	4 2-реберных	6 2-ребер	8 2-ребер	10 2-ребер	12 2-гранных	14 2-ребер	16 2-гранных

• Коксетер, Х. С. М. и Мозер, У. О. Дж.; Генераторы и соотношения для дискретных групп (1965), особенно стр. 67–80.
• Коксетер, HSM (1991), Правильные комплексные многогранники , Cambridge University Press, ISBN 0-521-39490-2
• Коксетер, Х. С. М. и Шепард, Г. К.; Портреты семейства сложных многогранников, Leonardo Vol 25, No 3/4, (1992), стр. 239–244,
• Шепард, GC; Правильные комплексные многогранники , Proc. London math. Soc. Series 3, Vol 2, (1952), стр. 82–97.
• Шепард, GC ; Тодд, JA (1954), "Конечные унитарные группы отражений", Canadian Journal of Mathematics , 6 : 274–304, doi :10.4153/cjm-1954-028-3, MR  0059914
• Густав И. Лерер и Дональд Э. Тейлор, «Группы единой рефлексии» , Cambridge University Press, 2009