Референтная модель атмосферы

Референтная атмосферная модель описывает, как изменяются свойства идеального газа (а именно: давление, температура, плотность и молекулярный вес) атмосферы, в первую очередь в зависимости от высоты , а иногда также в зависимости от широты , дня года и т. д. Статическая атмосферная модель имеет более ограниченную область, исключая время. Стандартная атмосфера определяется Всемирной метеорологической организацией как «гипотетическое вертикальное распределение атмосферной температуры, давления и плотности, которое, по международному соглашению, является примерно репрезентативным для круглогодичных условий в средних широтах ».

Типичное применение — в качестве основы для калибровки барометрических высотомеров , расчетов летно-технических характеристик самолетов, проектирования самолетов и ракет, баллистических таблиц и метеорологических диаграмм». [1]

Например, Стандартная атмосфера США выводит значения температуры воздуха, давления и плотности массы в зависимости от высоты над уровнем моря.

Другие статические атмосферные модели могут иметь другие выходные данные или зависеть от входных данных помимо высоты.

Основные предположения

Газ, из которого состоит атмосфера, обычно считается идеальным газом , то есть:

ρ = М П Р Т {\displaystyle \rho ={\frac {MP}{RT}}}

Где ρ — плотность массы, M — средняя молекулярная масса, P — давление, T — температура, а R — постоянная идеального газа.

Газ удерживается на месте так называемыми " гидростатическими " силами. То есть, для определенного слоя газа на некоторой высоте: направленная вниз (к планете) сила его веса, направленная вниз сила, оказываемая давлением в слое над ним, и направленная вверх сила, оказываемая давлением в слое под ним, все в сумме равны нулю. Математически это:

П А − ( П + г П ) А − ( ρ А г час ) г 0 = 0 {\displaystyle PA-(P+{\text{d}}P)A-(\rho A{\text{d}}h)g_{0}=0\,}
г П = − г 0 ρ г час {\displaystyle {\text{d}}P=-g_{0}\rho {\text{d}}h\,}

Наконец, эти переменные, описывающие систему, не изменяются со временем, т.е. это статическая система.

g_0 , гравитационное ускорение используется здесь как константа, с тем же значением, что и стандартная гравитация (среднее ускорение под действием силы тяжести на поверхности Земли или другого большого тела). Для простоты оно не меняется в зависимости от широты, высоты или местоположения. Изменение из-за всех этих факторов составляет около 1% до 50 км. Более сложные модели учитывают эти изменения.

Некоторые примеры

В зависимости от модели некоторые свойства газа можно считать постоянными по отношению к высоте.

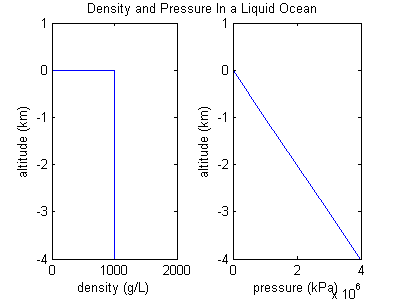
Пример океана

Если плотность газа постоянна, то он на самом деле не ведет себя как газ. Вместо этого он ведет себя как несжимаемая жидкость , или жидкость , и эта ситуация больше похожа на океан. Если предположить, что плотность постоянна, то график давления в зависимости от высоты будет иметь сохраняющийся наклон, поскольку вес океана над головой прямо пропорционален его глубине.

Изотермически-баротропное приближение и масштаб высоты

Эта атмосферная модель предполагает, что как молекулярный вес, так и температура постоянны в широком диапазоне высот. Такую модель можно назвать изотермической (постоянная температура). Подстановка постоянного молекулярного веса и постоянной температуры в уравнение для закона идеального газа приводит к тому, что плотность и давление, две оставшиеся переменные, зависят только друг от друга. По этой причине эту модель можно также назвать баротропной (плотность зависит только от давления).

Для изотермически-баротропной модели плотность и давление оказываются экспоненциальными функциями высоты. Увеличение высоты, необходимое для того, чтобы P или ρ упали до 1/ e от своего начального значения, называется высотой шкалы :

ЧАС = Р Т М г 0 {\displaystyle H={\frac {RT}{Mg_{0}}}}

где R — идеальная газовая постоянная, T — температура, M — средний молекулярный вес, а g 0 — ускорение свободного падения на поверхности планеты. Используя значения T =273 K и M =29 г/моль как характеристики атмосферы Земли, H = RT / Mg = (8,315*273)/(29*9,8) = 7,99, или около 8 км, что по совпадению является приблизительной высотой Эвереста .

Для изотермической атмосферы, или около 63% общей массы атмосферы находится между поверхностью планеты и одной масштабной высотой. (Общая масса воздуха ниже определенной высоты рассчитывается путем интегрирования по функции плотности.) ( 1 − 1 е ) {\displaystyle (1-{\frac {1}{e}})}

В примере с океаном был резкий переход в плотности наверху или «поверхности» океана. Однако для атмосфер, состоящих из газа, нет эквивалентного резкого перехода или края. Газовые атмосферы просто становятся все менее и менее плотными, пока они не станут настолько тонкими, что станут пространством.

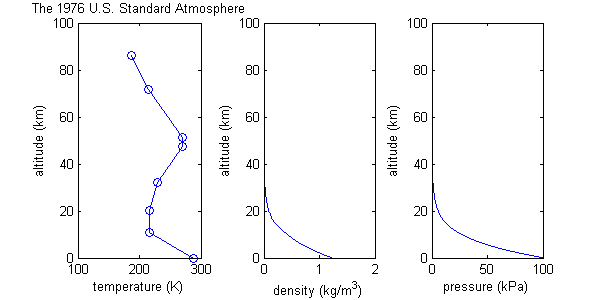
Стандартная атмосфера США

Модель стандартной атмосферы США начинается со многих из тех же предположений, что и изотермически-баротропная модель, включая поведение идеального газа и постоянный молекулярный вес, но она отличается определением более реалистичной температурной функции, состоящей из восьми точек данных, соединенных прямыми линиями; т. е. областей постоянного градиента температуры. (См. график.) Конечно, реальная атмосфера не имеет распределения температуры с такой точной формой. Температурная функция является приближением. Затем значения давления и плотности рассчитываются на основе этой температурной функции, а постоянные градиенты температуры помогают упростить некоторые математические вычисления.

Глобальная эталонная атмосферная модель НАСА

Глобальная эталонная атмосферная модель Земли NASA Earth (Earth-GRAM) была разработана Центром космических полетов им. Маршалла для обеспечения эталонной атмосферы, которая, в отличие от стандартных атмосфер, допускает географическую изменчивость, широкий диапазон высот (от поверхности до орбитальных высот), а также различные месяцы и время суток. Она также может моделировать пространственные и временные возмущения атмосферных параметров из-за турбулентности и других явлений атмосферных возмущений. Она доступна [2] в компьютерном коде, написанном на языке Fortran . [3] Серия GRAM также включает атмосферные модели для планет Венеры , Марса и Нептуна и луны Сатурна , Титана . [4]

Геопотенциальная высота

Гравитационное ускорение g (z) уменьшается с высотой, поскольку движение вверх означает удаление от центра планеты.

г ( з ) = Г м е ( г е + з ) 2 {\displaystyle g(z)={\frac {Gm_{e}}{(r_{e}+z)^{2}}}}

Эту проблему уменьшения g можно решить, определив преобразование из реальной геометрической высоты z в абстракцию, называемую «геопотенциальной высотой» h , определяемую следующим образом:

час = г е з г е + з {\displaystyle h={\frac {r_{e}z}{r_{e}+z}}}

h имеет свойство

г ( з ) г з = г 0 г час {\displaystyle {\frac {}{}}g(z)dz=g_{0}dh} где г 0 = г ( 0 ) = Г м е г е 2 {\displaystyle g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}}

По сути, это означает, что объем работы, выполненной для подъема пробной массы m на высоту z через атмосферу, где сила тяжести уменьшается с высотой, равен объему работы, выполненной для подъема той же массы на высоту h через атмосферу, где g волшебным образом остается равным g0 , его значению на уровне моря.

Эта геопотенциальная высота h затем используется вместо геометрической высоты z в гидростатических уравнениях.

Распространенные модели

Смотрите также

Ссылки

  1. ^ Национальное управление океанических и атмосферных исследований ; Национальное управление по аэронавтике и исследованию космического пространства ; Военно-воздушные силы США (октябрь 1976 г.), Стандартная атмосфера США, 1976 (PDF) , Вашингтон, округ Колумбия: Типография правительства США, стр. xiv
  2. ^ "Earth Global Reference Atmospheric Model (Earth-Gram) 2010", Каталог программного обеспечения 2015–2016 , NASA – Technology Transfer Program , получено 16 августа 2016 г.
  3. ^ Лесли, Ф. У.; Джастус, К. Г. (июнь 2011 г.), Глобальная эталонная атмосферная модель Земли Центра космических полетов им. Маршалла НАСА — версия 2010 г. (PDF) , NASA/TM — 2011–216467, Центр космических полетов им. Маршалла, Алабама: Национальное управление по аэронавтике и исследованию космического пространства , дата обращения 15 августа 2016 г.
  4. ^ Justh, Hilary L.; Justus, CG; Keller, Vernon W. (2006), «Глобальные эталонные атмосферные модели, включая термосферы, для Марса, Венеры и Земли», Конференция специалистов по астродинамике AIAA/AAS; 21–24 августа 2006 г.; Keystone, CO; Соединенные Штаты Америки , doi : 10.2514/6.2006-6394, hdl : 2060/20060048492
На Викискладе есть медиафайлы по теме «Справочная модель атмосферы» .
  • Общедоступное авиационное программное обеспечение – Вывод гидростатических уравнений, используемых в Стандартной атмосфере США 1976 года
  • Код FORTRAN для расчета стандартной атмосферы США
  • Обзор атмосферных моделей NASA GSFC
  • Различные модели в NASA GSFC ModelWeb
  • Глобальная эталонная модель атмосферы Земли (Earth-GRAM 2010)
Взято с "https://en.wikipedia.org/w/index.php?title=Эталонная_атмосферная_модель&oldid=1249060907"