Выпрямленные 9-симплексы

9-симплекс	Выпрямленный 9-симплекс
Биректифицированный 9-симплекс	Триректифицированный 9-симплекс	Квадриректифицированный 9-симплекс
Ортогональные проекции в плоскости Коксетера A 9

В девятимерной геометрии выпрямленный 9-симплекс — это выпуклый однородный 9-многогранник , являющийся выпрямлением правильного 9-симплекса .

Эти многогранники являются частью семейства из 271 однородных 9-мерных многогранников с симметрией _A9 .

Существуют уникальные 4 степени спрямлений. Вершины спрямленного 9-симплекса расположены в центрах ребер 9-симплекса. Вершины биспрямленного 9-симплекса расположены в центрах треугольных граней 9-симплекса. Вершины триспрямленного 9-симплекса расположены в центрах тетраэдрических ячеек 9-симплекса. Вершины квадриспрямленного 9-симплекса расположены в центрах 5 ячеек 9-симплекса.

Выпрямленный 9-симплекс
Тип	однородный 9-многогранник
Символ Шлефли	т 1 {3,3,3,3,3,3,3,3,3}
Диаграммы Коксетера-Дынкина
8-гранный	20
7-гранный	135
6-гранный	480
5-гранный	1050
4-х гранный	1512
Клетки	1470
Лица	960
Края	360
Вершины	45
Вершинная фигура	8-симплексная призма
Петри полигон	декагон
Группы Коксетера	А 9 , [3,3,3,3,3,3,3,3]
Характеристики	выпуклый

Выпрямленный 9-симплекс является вершинной фигурой 10- демикуба .

• Исправленный распадоттон (reday) (Джонатан Бауэрс) ^[1]

Декартовы координаты вершин выпрямленного 9-симплекса проще всего расположить в 10-пространстве как перестановки (0,0,0,0,0,0,0,0,1,1). Эта конструкция основана на гранях выпрямленного 10-ортоплекса .

ортографические проекции

Самолет Коксетера ​	А 9	А 8	А 7	А 6
График
Диэдральная симметрия	[10]	[9]	[8]	[7]
Самолет Коксетера​	А 5	А 4	А 3	А 2
График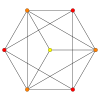
Диэдральная симметрия	[6]	[5]	[4]	[3]

Биректифицированный 9-симплекс
Тип	однородный 9-многогранник
Символ Шлефли	т 2 {3,3,3,3,3,3,3,3,3}
Диаграммы Коксетера-Дынкина
8-гранный
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края	1260
Вершины	120
Вершинная фигура	{3}×{3,3,3,3,3}
Группы Коксетера	А 9 , [3,3,3,3,3,3,3,3]
Характеристики	выпуклый

Этот многогранник является вершинной фигурой для сот 1 _62. Его 120 вершин представляют собой число соприкосновений соответствующей гиперболической 9-мерной упаковки сфер .

• Биректифицированный распадоттон (бредей) (Джонатан Бауэрс) ^[2]

Декартовы координаты вершин 9-симплекса с двойным выпрямлением могут быть наиболее просто расположены в 10-пространстве как перестановки (0,0,0,0,0,0,0,1,1,1). Эта конструкция основана на гранях 10-ортоплекса с двойным выпрямлением .

ортографические проекции

Самолет Коксетера ​	А 9	А 8	А 7	А 6
График
Диэдральная симметрия	[10]	[9]	[8]	[7]
Самолет Коксетера​	А 5	А 4	А 3	А 2
График
Диэдральная симметрия	[6]	[5]	[4]	[3]

Триректифицированный 9-симплекс
Тип	однородный 9-многогранник
Символ Шлефли	т 3 {3,3,3,3,3,3,3,3,3}
Диаграммы Коксетера-Дынкина
8-гранный
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края
Вершины
Вершинная фигура	{3,3}×{3,3,3,3}
Группы Коксетера	А 9 , [3,3,3,3,3,3,3,3]
Характеристики	выпуклый

• Триректифицированный распадоттон (тредей) (Джонатан Бауэрс) ^[3]

Декартовы координаты вершин триректифицированного 9-симплекса могут быть наиболее просто расположены в 10-пространстве как перестановки (0,0,0,0,0,0,1,1,1,1). Эта конструкция основана на гранях триректифицированного 10-ортоплекса .

ортографические проекции

Самолет Коксетера ​	А 9	А 8	А 7	А 6
График
Диэдральная симметрия	[10]	[9]	[8]	[7]
Самолет Коксетера​	А 5	А 4	А 3	А 2
График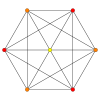
Диэдральная симметрия	[6]	[5]	[4]	[3]

Квадриректифицированный 9-симплекс
Тип	однородный 9-многогранник
Символ Шлефли	т 4 {3,3,3,3,3,3,3,3,3}
Диаграммы Коксетера-Дынкина	или
8-гранный
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края
Вершины
Вершинная фигура	{3,3,3}×{3,3,3}
Группы Коксетера	А 9 ×2, [[3 8 ]]
Характеристики	выпуклый

• Quadrirectified decayоттон
• Икосайоттон (icoy) (Джонатан Бауэрс) ^[4]

Декартовы координаты вершин квадриректифицированного 9-симплекса проще всего расположить в 10-пространстве как перестановки (0,0,0,0,0,1,1,1,1,1). Эта конструкция основана на гранях квадриректифицированного 10-ортоплекса .

ортографические проекции

Самолет Коксетера ​	А 9	А 8	А 7	А 6
График
Диэдральная симметрия	[10]	[9]	[8]	[7]
Самолет Коксетера​	А 5	А 4	А 3	А 2
График
Диэдральная симметрия	[6]	[5]	[4]	[3]

• HSM Коксетер :
  • HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
• Клитцинг, Ричард. «9D однородные многогранники (полиетты)».o3x3o3o3o3o3o3o3o - редай, o3o3x3o3o3o3o3o3o - бредай, o3o3o3x3o3o3o3o3o - тредей, o3o3o3o3x3o3o3o3o - icoy

• Многогранники различных размерностей
• Многомерный глоссарий