Инверсия населения
В физике , в частности в статистической механике , инверсия населенности происходит, когда система (например, группа атомов или молекул ) находится в состоянии, в котором больше членов системы находятся в более высоких, возбужденных состояниях, чем в более низких, невозбужденных энергетических состояниях . Это называется «инверсией», потому что во многих знакомых и часто встречающихся физических системах это невозможно. Эта концепция имеет фундаментальное значение в лазерной науке, поскольку создание инверсии населенности является необходимым шагом в работе стандартного лазера .
Распределения Больцмана и тепловое равновесие
Чтобы понять концепцию инверсии населенности, необходимо понимать некоторые аспекты термодинамики и то, как свет взаимодействует с веществом . Для этого полезно рассмотреть очень простую совокупность атомов , образующих лазерную среду .
Предположим, что имеется группа из N атомов, каждый из которых способен находиться в одном из двух энергетических состояний : либо
- Основное состояние с энергией E 1 ; или
- Возбужденное состояние с энергией E 2 , при этом E 2 > E 1 .
Число этих атомов, находящихся в основном состоянии, определяется как N 1 , а число в возбужденном состоянии — как N 2 . Поскольку всего имеется N атомов,
Разница энергий между двумя состояниями определяется выражением
определяет характерную частоту света, который будет взаимодействовать с атомами; Это задается соотношением
h — постоянная Планка .
Если группа атомов находится в тепловом равновесии , то с помощью статистики Максвелла-Больцмана можно показать , что отношение числа атомов в каждом состоянии определяется отношением двух распределений Больцмана , фактором Больцмана:
где T — термодинамическая температура группы атомов, k — постоянная Больцмана , а g 1 и g 2 — вырождения каждого состояния.
Можно рассчитать отношение населенностей двух состояний при комнатной температуре ( T ≈ 300 К ) для разности энергий Δ E , соответствующей свету с частотой, соответствующей видимому свету ( ν ≈ 5 × 10 14 Гц ). В этом случае Δ E = E 2 − E 1 ≈ 2,07 эВ, а kT ≈ 0,026 эВ. Поскольку E 2 − E 1 ≫ kT , то отсюда следует, что аргумент экспоненты в приведенном выше уравнении является большим отрицательным числом, и, как таковое, N 2 / N 1 исчезающе мало; т. е. в возбужденном состоянии почти нет атомов. Таким образом, при тепловом равновесии видно, что состояние с более низкой энергией более заселено, чем состояние с более высокой энергией, и это нормальное состояние системы. По мере увеличения T число электронов в состоянии с высокой энергией ( N 2 ) увеличивается, но N 2 никогда не превышает N 1 для системы, находящейся в тепловом равновесии; напротив, при бесконечной температуре заселенности N 2 и N 1 становятся равными. Другими словами, инверсия населенности ( N 2 / N 1 > 1 ) никогда не может существовать для системы, находящейся в тепловом равновесии. Поэтому для достижения инверсии населенности требуется перевести систему в неравновесное состояние.
Взаимодействие света с материей
Существует три типа возможных взаимодействий между системой атомов и светом, которые представляют интерес:
Поглощение
Если свет ( фотоны ) частоты ν 12 проходит через группу атомов, существует вероятность поглощения света электронами, находящимися в основном состоянии, что приведет к их возбуждению до более высокого энергетического состояния. Скорость поглощения пропорциональна плотности излучения света, а также числу атомов, находящихся в данный момент в основном состоянии, N 1 .
Спонтанное излучение
Если атомы находятся в возбужденном состоянии, то спонтанные события распада в основное состояние будут происходить со скоростью, пропорциональной N 2 , числу атомов в возбужденном состоянии. Разница энергий между двумя состояниями Δ E 21 испускается атомом в виде фотона с частотой ν 21 , как указано в приведенном выше соотношении частоты и энергии.
Фотоны испускаются стохастически , и нет фиксированного фазового соотношения между фотонами, испускаемыми группой возбужденных атомов; другими словами, спонтанное излучение некогерентно . При отсутствии других процессов число атомов в возбужденном состоянии в момент времени t определяется как
где N 2 (0) — число возбужденных атомов в момент времени t = 0, а τ 21 — среднее время жизни перехода между двумя состояниями.
Вынужденное излучение
Если атом уже находится в возбужденном состоянии, он может быть возбужден прохождением фотона с частотой ν 21 , соответствующей энергетической щели Δ E перехода из возбужденного состояния в основное состояние. В этом случае возбужденный атом релаксирует в основное состояние и производит второй фотон с частотой ν 21 . Первоначальный фотон не поглощается атомом, и поэтому результатом являются два фотона с одинаковой частотой. Этот процесс известен как вынужденное излучение .
В частности, возбужденный атом будет действовать как небольшой электрический диполь, который будет колебаться с внешним полем. Одним из последствий этого колебания является то, что оно побуждает электроны распадаться до состояния с самой низкой энергией. Когда это происходит из-за наличия электромагнитного поля от фотона, фотон испускается в той же фазе и направлении, что и «стимулирующий» фотон, и это называется стимулированным излучением.
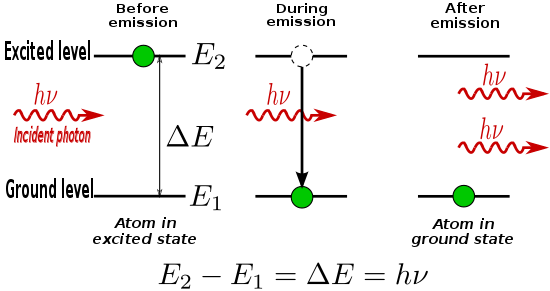
Скорость, с которой происходит вынужденное излучение, пропорциональна числу атомов N 2 в возбужденном состоянии и плотности излучения света. Альберт Эйнштейн показал, что базовая вероятность того, что фотон вызовет вынужденное излучение в одном возбужденном атоме , в точности равна вероятности поглощения фотона атомом в основном состоянии. Поэтому, когда число атомов в основном и возбужденном состояниях равно, скорость вынужденного излучения равна скорости поглощения для данной плотности излучения.
Критическая деталь вынужденного излучения заключается в том, что индуцированный фотон имеет ту же частоту и фазу , что и падающий фотон. Другими словами, два фотона когерентны . Именно это свойство обеспечивает оптическое усиление и создание лазерной системы. Во время работы лазера происходят все три взаимодействия света и вещества, описанные выше. Первоначально атомы переводятся из основного состояния в возбужденное с помощью процесса, называемого накачкой , описанного ниже. Некоторые из этих атомов распадаются посредством спонтанного излучения, высвобождая некогерентный свет в виде фотонов с частотой ν . Эти фотоны возвращаются в лазерную среду, обычно с помощью оптического резонатора . Некоторые из этих фотонов поглощаются атомами в основном состоянии, и фотоны теряются в процессе лазера. Однако некоторые фотоны вызывают вынужденное излучение в атомах в возбужденном состоянии, высвобождая другой когерентный фотон. По сути, это приводит к оптическому усилению .
Если число фотонов, усиливаемых за единицу времени, больше числа поглощаемых фотонов, то конечным результатом является непрерывно увеличивающееся число производимых фотонов; говорят, что лазерная среда имеет коэффициент усиления больше единицы.
Вспомним из описаний поглощения и вынужденного излучения выше, что скорости этих двух процессов пропорциональны числу атомов в основном и возбужденном состояниях, N 1 и N 2 соответственно. Если основное состояние имеет большую заселенность, чем возбужденное состояние ( N 1 > N 2 ), то процесс поглощения доминирует, и происходит чистое затухание фотонов. Если заселенности двух состояний одинаковы ( N 1 = N 2 ), скорость поглощения света точно уравновешивает скорость излучения; тогда говорят, что среда оптически прозрачна .
Если состояние с более высокой энергией имеет большую заселенность, чем состояние с более низкой энергией ( N 1 < N 2 ), то процесс испускания доминирует, и свет в системе претерпевает чистое увеличение интенсивности. Таким образом, ясно, что для получения более высокой скорости стимулированного испускания, чем поглощения, требуется, чтобы отношение заселенностей двух состояний было таким, что N 2 / N 1 > 1; Другими словами, для работы лазера требуется инверсия заселенности.
Правила отбора
Многие переходы, включающие электромагнитное излучение, строго запрещены в квантовой механике. Разрешенные переходы описываются так называемыми правилами отбора , которые описывают условия, при которых разрешен радиационный переход. Например, переходы разрешены только если Δ S = 0, где S — полный спиновый угловой момент системы. В реальных материалах другие эффекты, такие как взаимодействие с кристаллической решеткой, вмешиваются, чтобы обойти формальные правила, предоставляя альтернативные механизмы. В этих системах запрещенные переходы могут происходить, но обычно с более низкой скоростью, чем разрешенные переходы. Классическим примером является фосфоресценция , когда материал имеет основное состояние с S = 0, возбужденное состояние с S = 0 и промежуточное состояние с S = 1. Переход из промежуточного состояния в основное состояние путем испускания света происходит медленно из-за правил отбора. Таким образом, испускание может продолжаться после того, как внешнее освещение удалено. Напротив, флуоресценция в материалах характеризуется испусканием, которое прекращается при удалении внешнего освещения.
Переходы, не связанные с поглощением или испусканием излучения, не подвержены влиянию правил отбора. Безызлучательный переход между уровнями, например, между возбужденными состояниями S = 0 и S = 1, может происходить достаточно быстро, чтобы откачать часть популяции S = 0, прежде чем она спонтанно вернется в основное состояние.
Существование промежуточных состояний в материалах имеет существенное значение для техники оптической накачки лазеров (см. ниже).
Создание инверсии населенности
Для работы лазера требуется инверсия населенности , но ее невозможно достичь в указанной выше теоретической группе атомов с двумя уровнями энергии, когда они находятся в тепловом равновесии. Фактически, любой метод, с помощью которого атомы напрямую и непрерывно возбуждаются из основного состояния в возбужденное состояние (например, оптическое поглощение), в конечном итоге достигнет равновесия с девозбуждающими процессами спонтанного и стимулированного излучения. В лучшем случае может быть достигнута равная населенность двух состояний, N 1 = N 2 = N /2, что приводит к оптической прозрачности, но не к чистому оптическому усилению.
Трехуровневые лазеры
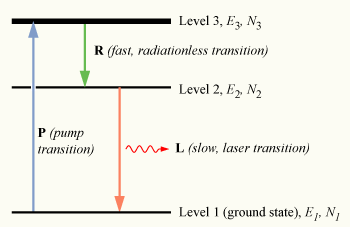
Для достижения длительных неравновесных условий необходимо использовать косвенный метод заселения возбужденного состояния. Чтобы понять, как это делается, рассмотрим немного более реалистичную модель — трехуровневого лазера . Снова рассмотрим группу из N атомов, на этот раз каждый из которых может находиться в любом из трех энергетических состояний, уровней 1, 2 и 3, с энергиями E 1 , E 2 и E 3 и заселенностями N 1 , N 2 и N 3 соответственно.
Предположим, что E 1 < E 2 < E 3 ; то есть энергия уровня 2 лежит между энергией основного состояния и уровнем 3.
Первоначально система атомов находится в тепловом равновесии, и большинство атомов будут находиться в основном состоянии, т. е. N 1 ≈ N , N 2 ≈ N 3 ≈ 0 . Если атомы подвергаются воздействию света с частотой , процесс оптического поглощения возбудит электроны из основного состояния на уровень 3. Этот процесс называется накачкой и не обязательно всегда напрямую включает поглощение света; могут использоваться другие методы возбуждения лазерной среды, такие как электрический разряд или химические реакции. Уровень 3 иногда называют уровнем накачки или полосой накачки , а энергетический переход E 1 → E 3 - переходом накачки , который показан стрелкой, обозначенной P на диаграмме справа.
При накачке среды значительное число атомов перейдет на уровень 3, так что N 3 > 0. Чтобы среда была пригодна для работы лазера, необходимо, чтобы эти возбужденные атомы быстро распадались на уровень 2. Энергия, выделяемая при этом переходе, может испускаться в виде фотона (спонтанное излучение), однако на практике переход 3 → 2 , называемый эффектом Оже (обозначен как R на схеме), обычно является безызлучательным , при этом энергия передается колебательному движению ( теплу ) основного материала, окружающего атомы, без генерации фотона.
Электрон на уровне 2 может распасться путем спонтанного излучения в основное состояние, высвобождая фотон с частотой ν 12 (задается как E 2 − E 1 = hν 12 ), что показано как переход L , называемый лазерным переходом на диаграмме. Если время жизни этого перехода τ 21 намного больше времени жизни безызлучательного перехода 3 → 2 τ 32 (если τ 21 ≫ τ 32 , известное как благоприятное отношение времени жизни ), заселенность E 3 будет по существу равна нулю ( N 3 ≈ 0 ), и заселенность атомов в возбужденном состоянии будет накапливаться на уровне 2 ( N 2 > 0 ). Если более половины атомов N могут быть накоплены в этом состоянии, это превысит заселенность основного состояния N 1 . Таким образом, между уровнями 1 и 2 достигается инверсия населенности ( N 2 > N 1 ), и может быть получено оптическое усиление на частоте ν 21 .
Поскольку по крайней мере половина популяции атомов должна быть возбуждена из основного состояния для получения инверсии населенности, лазерная среда должна быть очень сильно накачана. Это делает трехуровневые лазеры довольно неэффективными, несмотря на то, что это первый тип лазера, который был открыт (на основе рубиновой лазерной среды Теодором Майманом в 1960 году). Трехуровневая система также может иметь излучательный переход между уровнями 3 и 2 и неизлучательный переход между 2 и 1. В этом случае требования к накачке слабее. На практике большинство лазеров являются четырехуровневыми лазерами , описанными ниже.
Четырехуровневый лазер

Здесь есть четыре энергетических уровня, энергии E 1 , E 2 , E 3 , E 4 и популяции N 1 , N 2 , N 3 , N 4 соответственно. Энергии каждого уровня таковы, что E 1 < E 2 < E 3 < E 4 .
В этой системе переход накачки P возбуждает атомы в основном состоянии (уровень 1) в полосу накачки (уровень 4). С уровня 4 атомы снова распадаются посредством быстрого безызлучательного перехода Ra на уровень 3. Поскольку время жизни лазерного перехода L велико по сравнению со временем жизни Ra ( τ 32 ≫ τ 43 ), на уровне 3 ( верхнем лазерном уровне ) накапливается популяция , которая может релаксировать посредством спонтанного или стимулированного излучения на уровень 2 ( нижний лазерный уровень ). Этот уровень также имеет быстрый безызлучательный распад Rb в основное состояние.
Как и прежде, наличие быстрого безызлучательного распада приводит к быстрому истощению популяции полосы накачки ( N 4 ≈ 0). В четырехуровневой системе любой атом на нижнем лазерном уровне E 2 также быстро девозбуждается, что приводит к незначительной популяции в этом состоянии ( N 2 ≈ 0). Это важно, поскольку любая заметная популяция, накапливающаяся на уровне 3, верхнем лазерном уровне, будет формировать инверсию населенности относительно уровня 2. То есть, пока N 3 > 0, то N 3 > N 2 , и достигается инверсия населенности. Таким образом, оптическое усиление и работа лазера могут происходить на частоте ν 32 ( E 3 − E 2 = hν 32 ).
Поскольку для формирования инверсии населенности необходимо возбудить всего несколько атомов на верхнем лазерном уровне, четырехуровневый лазер гораздо эффективнее трехуровневого, и большинство практических лазеров относятся к этому типу. В действительности в лазерном процессе может быть задействовано гораздо больше четырех энергетических уровней, причем между этими уровнями происходят сложные процессы возбуждения и релаксации. В частности, полоса накачки может состоять из нескольких отдельных энергетических уровней или континуума уровней, что позволяет осуществлять оптическую накачку среды в широком диапазоне длин волн.
Обратите внимание, что как в трех-, так и в четырехуровневых лазерах энергия перехода накачки больше, чем у лазерного перехода. Это означает, что если лазер накачивается оптически, частота света накачки должна быть больше, чем частота результирующего лазерного света. Другими словами, длина волны накачки короче длины волны лазера. В некоторых средах возможно использовать множественное поглощение фотонов между множественными переходами с более низкой энергией для достижения уровня накачки; такие лазеры называются лазерами с ап-конверсией .
Хотя во многих лазерах лазерный процесс включает переход атомов между различными электронными энергетическими состояниями, как описано в модели выше, это не единственный механизм, который может привести к лазерному действию. Например, существует много распространенных лазеров (например, лазеры на красителях , лазеры на углекислом газе ), где лазерная среда состоит из полных молекул, а энергетические состояния соответствуют колебательным и вращательным модам колебаний молекул. Это касается водных мазеров , которые встречаются в природе .
В некоторых средах возможно, накладывая дополнительное оптическое или микроволновое поле, использовать эффекты квантовой когерентности для снижения вероятности перехода из основного состояния в возбужденное. Эта техника, известная как лазерная генерация без инверсии , позволяет осуществлять оптическое усиление без создания инверсии населенности между двумя состояниями.
Другие методы создания инверсии населенности
Вынужденное излучение впервые было обнаружено в микроволновой области электромагнитного спектра, что дало начало аббревиатуре MASER (Microwave Amplification by Stimulated Emission of Radiation). В микроволновой области распределение Больцмана молекул по энергетическим состояниям таково, что при комнатной температуре все состояния заселены почти одинаково.
Чтобы создать инверсию населенности в этих условиях, необходимо выборочно удалить некоторые атомы или молекулы из системы на основе различий в свойствах. Например, в водородном мазере , хорошо известный 21 см волновой переход в атомарном водороде , где одинокий электрон переворачивает свое спиновое состояние с параллельного ядерному спину на антипараллельное, может быть использован для создания инверсии населенности, поскольку параллельное состояние имеет магнитный момент, а антипараллельное состояние — нет. Сильное неоднородное магнитное поле отделит атомы в более высоком энергетическом состоянии от пучка атомов в смешанном состоянии. Разделенная населенность представляет собой инверсию населенности, которая может демонстрировать стимулированные излучения.
Смотрите также
Ссылки
- Свелто, Орацио (1998). Принципы работы лазеров , 4-е изд. (перевод Дэвида Ханны), Спрингер. ISBN 0-306-45748-2






