Алгоритм Полларда ро

Алгоритм факторизации целых чисел

Алгоритм Ро Полларда — это алгоритм факторизации целых чисел . Он был изобретен Джоном Поллардом в 1975 году. ^[1] Он использует лишь небольшой объем памяти, а его ожидаемое время работы пропорционально квадратному корню наименьшего простого множителя факторизуемого составного числа .

Основные идеи

Алгоритм используется для факторизации числа , где — нетривиальный множитель. Многочлен по модулю , называемый (например, ), используется для генерации псевдослучайной последовательности . Важно отметить, что должно быть многочленом. Выбирается начальное значение, скажем, 2, и последовательность продолжается как , , , и т. д. Последовательность связана с другой последовательностью . Поскольку заранее неизвестно, эта последовательность не может быть явно вычислена в алгоритме. Тем не менее, в ней заключается основная идея алгоритма. $n=pq$ $p$ $n$ $g(x)$ $g(x)=(x^{2}+1){\bmod {n}}$ $g(x)$ $x_{1}=g(2)$ $x_{2}=g(g(2))$ $x_{3}=g(g(g(2)))$ $\{x_{k}{\bmod {p}}\}$ $p$

Поскольку число возможных значений для этих последовательностей конечно, и последовательность, которая равна mod , и последовательность в конечном итоге будут повторяться, даже если эти значения неизвестны. Если бы последовательности вели себя как случайные числа, парадокс дней рождения подразумевает, что число до того, как произойдет повторение, должно быть , где — число возможных значений. Таким образом, последовательность, скорее всего, повторится гораздо раньше, чем последовательность . Когда найдено такое, что но , число кратно , поэтому был найден нетривиальный делитель. ^[2] $\{x_{k}\}$ $n$ $\{x_{k}{\bmod {p}}\}$ $x_{k}$ $O({\sqrt {N}})$ $N$ $\{x_{k}{\bmod {p}}\}$ $\{x_{k}\}$ $k_{1},k_{2}$ $x_{k_{1}}\neq x_{k_{2}}$ $x_{k_{1}}\equiv x_{k_{2}}{\bmod {p}}$ $|x_{k_{1}}-x_{k_{2}}|$ $p$

Как только последовательность имеет повторяющееся значение, последовательность будет цикличной, поскольку каждое значение зависит только от предыдущего. Эта структура окончательного цикла дает начало названию «алгоритм rho» из-за сходства с формой греческой буквы ρ, когда значения , , и т. д. представлены как узлы в направленном графе . $x_{1}{\bmod {p}}$ $x_{2}{\bmod {p}}$

Это обнаруживается алгоритмом поиска цикла Флойда : сохраняются два узла и (т. е. и ). На каждом шаге один перемещается к следующему узлу в последовательности, а другой перемещается вперед на два узла. После этого проверяется , . Если он не равен 1, то это означает, что в последовательности есть повторение (т. е . Это работает, потому что если равен , то разность между и обязательно кратна . Хотя это всегда происходит в конечном итоге, полученный наибольший общий делитель (НОД) является делителем, отличным от 1. Это может быть он сам, поскольку две последовательности могут повторяться одновременно. В этом (редком) случае алгоритм терпит неудачу и может быть повторен с другим параметром. $i$ $j$ $x_{i}$ $x_{j}$ $\gcd(x_{i}-x_{j},n)\neq 1$ $\{x_{k}{\bmod {p}}\}$ $x_{i}{\bmod {p}}=x_{j}{\bmod {p}})$ $x_{i}{\bmod {p}}$ $x_{j}{\bmod {p}}$ $x_{i}$ $x_{j}$ $p$ $n$ $n$

Алгоритм

Алгоритм принимает в качестве входных данных $n$ , целое число , которое нужно разложить на множители; и ⁠ ⁠ $g(x)$ , многочлен от $x,$ вычисленный по модулю $n$ . В оригинальном алгоритме , но в настоящее время чаще используют . Выходными данными является либо нетривиальный множитель $n$ , либо неудача. $g(x)=(x^{2}-1){\bmod {n}}$ $g(x)=(x^{2}+1){\bmod {n}}$

Он выполняет следующие шаги: ^[2]

Псевдокод для алгоритма Полларда rho

 x ← 2 // начальное значение у ← х г ← 1 в то время как d = 1: х ← г(х) у ← г(г(у)) d ← НОД(|x - y|, n) если d = n: вернуть ошибку,  иначе : вернуть d

Здесь $x$ и $y$ соответствуют ⁠ ⁠ $x_{i}$ и ⁠ ⁠ $x_{j}$ в предыдущем разделе. Обратите внимание, что этот алгоритм может не найти нетривиальный множитель, даже если $n$ является составным. В этом случае метод можно попробовать снова, используя начальное значение x, отличное от 2 ( ) или другое ⁠ ⁠ , , с . $0\leq x<n$ $g(x)$ $g(x)=(x^{2}+b){\bmod {n}}$ $1\leq b<n-2$

Пример факторизации

Пусть и . $n=8051$ $g(x)=(x^{2}+1){\bmod {8}}051$

{\displaystyle n=253} — Пример факторизации ро-алгоритма Полларда для и с начальным значением 2. В примере используется алгоритм поиска цикла Флойда . $n=253$ $g(x)=x^{2}{\bmod {2}}53$

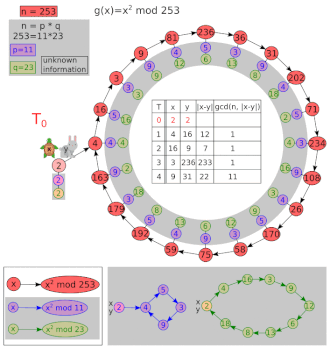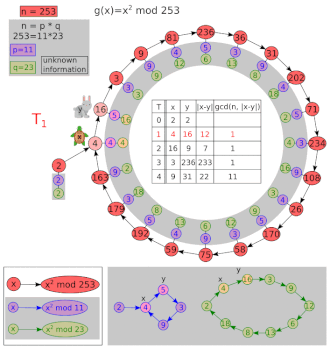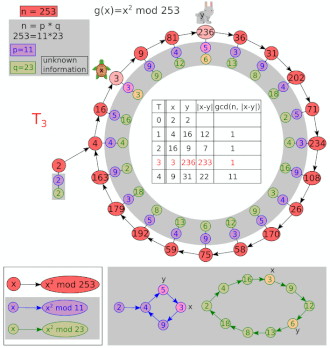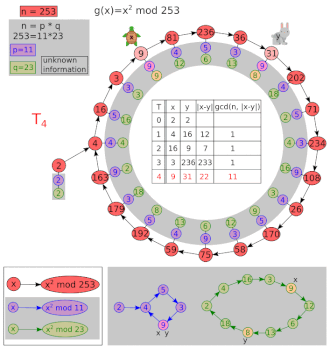
$я$	$х$	$у$	$НОД(\| x - y \|, 8051)$
1	5	26	1
2	26	7474	1
3	677	871	97
4	7474	1481	1

Теперь 97 — нетривиальный множитель 8051. Начальные значения, отличные от $x = y = 2,$ могут дать сомножитель (83) вместо 97. Одна дополнительная итерация показана выше, чтобы прояснить, что $y$ движется в два раза быстрее, чем $x$ . Обратите внимание, что даже после повторения НОД может вернуться к 1.

Варианты

В 1980 году Ричард Брент опубликовал более быстрый вариант алгоритма rho. Он использовал те же основные идеи, что и Поллард, но другой метод обнаружения цикла, заменив алгоритм поиска цикла Флойда на связанный метод поиска цикла Брента . ^[3] CLRS дает эвристический анализ и условия отказа ( находится тривиальный делитель ). ^[2] $n$

Дальнейшее улучшение было сделано Поллардом и Брентом. Они заметили, что если , то также для любого положительного целого числа ⁠ ⁠ . В частности, вместо того, чтобы вычислять на каждом шаге, достаточно определить ⁠ ⁠ как произведение 100 последовательных членов по модулю ⁠ ⁠ , а затем вычислить один . Значительное ускорение достигается за счет замены 100 шагов $НОД на 99 умножений по модулю$ ⁠ ⁠ и один $НОД$ . Иногда это может привести к сбою алгоритма из-за введения повторяющегося множителя, например, когда ⁠ ⁠ является квадратом . Но тогда достаточно вернуться к предыдущему члену $НОД$ , где , и использовать обычный алгоритм ρ оттуда. ^{[примечание 1]} $\gcd(a,n)>1$ $\gcd(ab,n)>1$ $b$ $\gcd(|x-y|,n)$ $z$ $|x-y|$ $n$ $\gcd(z,n)$ $n$ $n$ $\gcd(z,n)=1$

Приложение

Алгоритм очень быстр для чисел с малыми множителями, но медленнее в случаях, когда все множители велики. Самым выдающимся успехом алгоритма ρ стала факторизация в 1980 году числа Ферма $F 8$ = 1238926361552897 × 93461639715357977769163558199606896584051237541638188580280321. ^[4] Алгоритм ρ был хорошим выбором для $F 8$ , потому что простой множитель $p$ = 1238926361552897 намного меньше другого множителя. Факторизация заняла 2 часа на UNIVAC 1100/42 . ^[4]

Пример: факторинг $н$ = 10403 = 101 · 103

В следующей таблице показаны числа, полученные алгоритмом, начиная с и используя полином . Третий и четвертый столбцы таблицы содержат дополнительную информацию, не известную алгоритму. Они включены, чтобы показать, как работает алгоритм. $x=2$ $g(x)=(x^{2}+1){\bmod {1}}0403$

⁠ ⁠ $x$	⁠ ⁠ $y$	⁠ ⁠ $x{\bmod {1}}01$	⁠ ⁠ $y{\bmod {1}}01$	шаг
2	2	2	2	0
5	2	5	2	1
26	2	26	2	2
677	26	71	26	3
598	26	93	26	4
3903	26	65	26	5
3418	26	85	26	6
156	3418	55	85	7
3531	3418	97	85	8
5168	3418	17	85	9
3724	3418	88	85	10
978	3418	69	85	11
9812	3418	15	85	12
5983	3418	24	85	13
9970	3418	72	85	14
236	9970	34	72	15
3682	9970	46	72	16
2016	9970	97	72	17
7087	9970	17	72	18
10289	9970	88	72	19
2594	9970	69	72	20
8499	9970	15	72	21
4973	9970	24	72	22
2799	9970	72	72	23

Первое повторение по модулю 101 равно 97, что происходит на шаге 17. Повторение не обнаруживается до шага 23, когда . Это приводит к тому, что , и находится множитель. $x\equiv y{\pmod {101}}$ $\gcd(x-y,n)=\gcd(2799-9970,n)$ $p=101$

Сложность

Если бы псевдослучайное число, встречающееся в алгоритме Полларда ρ, было бы фактическим случайным числом, то из этого следовало бы, что успех был бы достигнут в половине случаев, по парадоксу дня рождения в итерациях. Считается, что тот же анализ применим и к фактическому алгоритму rho, но это эвристическое утверждение, и строгий анализ алгоритма остается открытым. ^[5] $x=g(x)$ $O({\sqrt {p}})\leq O(n^{1/4})$

Смотрите также

Примечания

^ Упражнение 31.9-4 в CLRS

Ссылки

^ Поллард, Дж. М. (1975). «Метод Монте-Карло для факторизации» (PDF) . BIT Numerical Mathematics . 15 (3): 331– 334. doi :10.1007/bf01933667. S2CID 122775546.
^ abc Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. & Stein, Clifford (2009). "Раздел 31.9: Факторизация целых чисел". Введение в алгоритмы (третье изд.). Cambridge, MA: MIT Press. стр. 975–980 . ISBN 978-0-262-03384-8.(в этом разделе обсуждается только алгоритм Полларда rho).
^ Брент, Ричард П. (1980). «Улучшенный алгоритм факторизации Монте-Карло». BIT . 20 (2): 176– 184. doi :10.1007/BF01933190. S2CID 17181286.
^ ab Брент, RP; Поллард, JM (1981). «Факторизация восьмого числа Ферма». Математика вычислений . 36 (154): 627– 630. doi : 10.2307/2007666 . JSTOR 2007666.
^ Гэлбрейт, Стивен Д. (2012). «14.2.5 На пути к строгому анализу ро Полларда». Математика криптографии с открытым ключом. Cambridge University Press. С. 272– 273. ISBN 9781107013926..

Дальнейшее чтение

Бай, Ши; Брент, Ричард П. (январь 2008 г.). «Об эффективности метода Ро Полларда для дискретных логарифмов». Конференции по исследованиям и практике в области информационных технологий, т. 77. Симпозиум по теории Австралазии (CATS2008). Вуллонгонг. стр. 125–131 . Описывает улучшения, доступные с помощью различных итерационных функций и алгоритмов поиска циклов.
Кац, Джонатан; Линделл, Йехуда (2007). «Глава 8». Введение в современную криптографию . CRC Press.
Сэмюэл С. Вагстафф, младший (2013). Радость факторизации. Провиденс, Род-Айленд: Американское математическое общество. стр. 135–138 . ISBN 978-1-4704-1048-3.

Внешние ссылки

Подробная статья об алгоритме Полларда Rho, рассчитанная на аудиторию начального уровня.
Вайсштейн, Эрик В. «Метод факторизации Полларда по ро». MathWorld .
Реализация Java
О Полларде ро

[4] Упражнение 31.9-4 в CLRS

[1] Поллард, Дж. М. (1975). «Метод Монте-Карло для факторизации» (PDF) . BIT Numerical Mathematics . 15 (3): 331– 334. doi :10.1007/bf01933667. S2CID 122775546.

[:0-2] Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. & Stein, Clifford (2009). "Раздел 31.9: Факторизация целых чисел". Введение в алгоритмы (третье изд.). Cambridge, MA: MIT Press. стр. 975–980 . ISBN 978-0-262-03384-8.(в этом разделе обсуждается только алгоритм Полларда rho).

[3] Брент, Ричард П. (1980). «Улучшенный алгоритм факторизации Монте-Карло». BIT . 20 (2): 176– 184. doi :10.1007/BF01933190. S2CID 17181286.

[FotEFN-5] Брент, RP; Поллард, JM (1981). «Факторизация восьмого числа Ферма». Математика вычислений . 36 (154): 627– 630. doi : 10.2307/2007666 . JSTOR 2007666.

[6] Гэлбрейт, Стивен Д. (2012). «14.2.5 На пути к строгому анализу ро Полларда». Математика криптографии с открытым ключом. Cambridge University Press. С. 272– 273. ISBN 9781107013926..