Показатели неравенства доходов
Метрики неравенства доходов или метрики распределения доходов используются социологами для измерения распределения доходов и экономического неравенства среди участников конкретной экономики, например, экономики конкретной страны или мира в целом. В то время как различные теории могут пытаться объяснить, как возникает неравенство доходов, метрики неравенства доходов просто предоставляют систему измерений, используемую для определения дисперсии доходов. Понятие неравенства отличается от бедности [Примечание 1] и справедливости .
Распределение доходов всегда было центральной проблемой экономической теории и экономической политики . Классические экономисты, такие как Адам Смит , Томас Мальтус и Давид Рикардо, в основном интересовались распределением доходов по факторам, то есть распределением доходов между основными факторами производства , землей, трудом и капиталом. Его часто связывают с распределением богатства , хотя на неравенство богатства влияют и отдельные факторы .
Современные экономисты также обращались к этой проблеме, но больше интересовались распределением доходов между отдельными лицами и домохозяйствами. Важные теоретические и политические проблемы включают связь между неравенством доходов и экономическим ростом . В статье « Экономическое неравенство» обсуждаются социальные и политические аспекты вопросов распределения доходов.
Определение дохода
Все метрики, описанные ниже, применимы для оценки неравенства распределения различных видов ресурсов. Здесь основное внимание уделяется доходу как ресурсу. Поскольку существуют различные формы «дохода», исследуемый вид дохода должен быть четко описан.
Одной из форм дохода является общая сумма товаров и услуг, которые получает человек, и, таким образом, здесь не обязательно задействованы деньги или наличные. Если фермер в Уганде выращивает собственное зерно, это будет считаться доходом. Такие услуги, как здравоохранение и образование, также учитываются. Часто расходы или потребление (что одно и то же в экономическом смысле) используются для измерения дохода. Всемирный банк использует так называемые «обследования по измерению уровня жизни» [1] для измерения дохода. Они состоят из анкет с более чем 200 вопросами. Опросы были проведены в большинстве развивающихся стран .
Применительно к анализу неравенства доходов внутри стран, «доход» часто означает налогооблагаемый доход на одного человека или на одно домохозяйство. Здесь показатели неравенства доходов также могут использоваться для сравнения распределения доходов до и после налогообложения с целью измерения эффектов прогрессивных налоговых ставок.
Свойства показателей неравенства
В дискретном случае индекс экономического неравенства может быть представлен функцией I(x) , где x — это набор из n экономических значений (например, богатства или дохода) x={x 1 ,x 2 ,...,x n } , где x i — экономическое значение, связанное с «экономическим агентом» i .
В экономической литературе, посвященной неравенству, обычно постулируются четыре свойства, которым должна удовлетворять любая мера неравенства:
- Анонимность или симметрия
- Это предположение утверждает, что показатель неравенства не зависит от «маркировки» индивидов в экономике, и все, что имеет значение, — это распределение дохода. Например, в экономике, состоящей из двух человек, мистера Смита и миссис Джонс, где один из них имеет 60% дохода, а другой — 40%, показатель неравенства должен быть одинаковым, независимо от того, мистер Смит или миссис Джонс имеют долю в 40%. Это свойство отличает концепцию неравенства от концепции справедливости , где центральное значение имеет то, кто владеет определенным уровнем дохода и как он был получен. Показатель неравенства — это утверждение просто о том, как распределяется доход, а не о том, кем являются конкретные люди в экономике или какой доход они «заслуживают».
- Математически это обычно выражается так:
- где P(x) — любая перестановка x ;
- Масштабная независимость или однородность
- Это свойство говорит о том, что более богатые экономики не должны автоматически считаться более неравными по конструкции. Другими словами, если доход каждого человека в экономике удваивается (или умножается на любую положительную константу), то общая метрика неравенства не должна меняться. Конечно, то же самое относится и к более бедным экономикам. Метрика неравенства доходов должна быть независимой от совокупного уровня дохода. Это можно сформулировать так:
- где α — положительное действительное число.
- Независимость населения
- Аналогично, показатель неравенства доходов не должен зависеть от того, имеет ли экономика большое или малое население. Экономика с небольшим количеством людей не должна автоматически оцениваться показателем как более равная, чем большая экономика с большим количеством людей. Это означает, что показатель должен быть независимым от уровня населения. Обычно это записывается так:
- где — объединение x с (копией) самого себя .
- Принцип передачи
- Принцип Пигу–Дальтона , или принцип переноса, — это предположение, которое делает метрику неравенства фактически мерой неравенства. В своей слабой форме он гласит, что если некоторый доход передается от богатого человека бедному человеку, при этом сохраняется порядок рангов доходов, то измеряемое неравенство не должно увеличиваться. В своей сильной форме измеряемый уровень неравенства должен уменьшаться.
Другие полезные, но не обязательные свойства включают в себя:
- Неотрицательность
- Индекс I(x) больше или равен нулю.
- Эгалитарный ноль
- Индекс I(x) равен нулю в эгалитарном случае, когда все значения x i равны.
- Ограничено сверху максимальным неравенством
- Индекс I(x) достигает максимального значения при максимальном неравенстве (все x i равны нулю, кроме одного). Это значение обычно равно единице, поскольку число агентов n стремится к бесконечности.
- Подгрупповая разложимость [2]
- Это свойство гласит, что если множество агентов x разделить на два непересекающихся подмножества ( y и z ), то I(x) можно выразить как:
- где μ(x) и μ(y) — средние доходы x и y .
- и функции w являются скалярными весовыми функциями множеств y и z . В более сильном утверждении w y = μ y / μ x и w z = μ z / μ x .
Общие показатели неравенства доходов
Среди наиболее распространенных метрик, используемых для измерения неравенства, — индекс Джини (также известный как коэффициент Джини ), индекс Тейла и индекс Гувера . Они обладают всеми четырьмя свойствами, описанными выше.
Дополнительным свойством метрики неравенства, которое может быть желательным с эмпирической точки зрения, является свойство «разложимости». Это означает, что если конкретная экономика разбита на субрегионы и метрика неравенства вычисляется для каждого субрегиона отдельно, то мера неравенства для экономики в целом должна быть средневзвешенным значением регионального неравенства плюс член, пропорциональный неравенству в средних значениях регионов. (в более слабой форме это означает, что она должна быть явной функцией субрегионального неравенства, хотя и не обязательно линейной). Из вышеперечисленных индексов только индекс Тейла обладает этим свойством.
Поскольку эти показатели неравенства доходов являются сводной статистикой, которая стремится объединить все распределение доходов в единый индекс, информация об измеренном неравенстве сокращается. Это сокращение информации, конечно, является целью вычисления показателей неравенства, поскольку оно снижает сложность.
Более слабое снижение сложности достигается, если распределение доходов описывается долями общего дохода. Вместо того, чтобы указывать единую меру, исследуемое общество делится на сегменты, например, на квинтили (или любой другой процент населения). Обычно каждый сегмент содержит одинаковую долю получателей дохода. В случае неравного распределения дохода доли дохода, доступные в каждом сегменте, различны.
Во многих случаях индексы неравенства, упомянутые выше, вычисляются из таких сегментных данных без оценки неравенства внутри сегментов. Чем больше число сегментов (например, децилей вместо квинтилей), тем ближе измеренное неравенство распределения становится к реальному неравенству. (Если неравенство внутри сегментов известно, общее неравенство может быть определено теми метриками неравенства, которые обладают свойством быть «разложимыми».)
Квинтильные показатели неравенства удовлетворяют принципу переноса только в его слабой форме, поскольку любые изменения в распределении доходов за пределами соответствующих квинтилей не улавливаются этими показателями; имеет значение только распределение доходов между очень богатыми и очень бедными, тогда как неравенство в середине не играет никакой роли.
Подробности трех мер неравенства описаны в соответствующих статьях Википедии. Следующие подразделы охватывают их лишь кратко.
индекс Джини

Индекс Джини — это сводная статистика, которая измеряет, насколько справедливо распределены ресурсы среди населения ; доход — это основной пример. В дополнение к самодостаточному представлению индекса Джини мы даем два эквивалентных способа интерпретации этой сводной статистики: во-первых, с точки зрения процентильного уровня человека, который зарабатывает средний доллар , и, во-вторых, с точки зрения того, как меньший из двух случайно выбранных доходов сравнивается в среднем со средним доходом. [3]
Индекс Джини представляет собой сумму дефицита совокупного дохода по всем процентилям населения, упорядоченным по уровню дохода, от равной доли до каждого процентиля населения, причем этот суммарный дефицит делится на наибольшее возможное значение при полном неравенстве.
Диапазон индекса Джини составляет от 0 до 1 (0% и 100%), где 0 указывает на полное равенство, а 1 (100%) — на максимальное неравенство.
Индекс Джини является наиболее часто используемым индексом неравенства. Причина его популярности в том, что легко понять, как вычислить индекс Джини как отношение двух областей на диаграммах кривых Лоренца . Эта мера пытается охватить общую дисперсию дохода; однако она имеет тенденцию придавать разную степень важности нижнему, среднему и верхнему концам распределения. Недостатком индекса Джини является то, что он только сопоставляет число со свойствами диаграммы, но сама диаграмма не основана ни на какой модели процесса распределения. «Значение» индекса Джини можно понять только эмпирически. Кроме того, Джини не фиксирует, где в распределении возникает неравенство. В результате два совершенно разных распределения дохода могут иметь одинаковый индекс Джини.
соотношение 20:20

Соотношение 20:20 или 20/20 сравнивает, насколько богаче верхние 20% населения по сравнению с нижними 20% данного населения. Это может быть более показательным для фактического влияния неравенства на население, поскольку это уменьшает влияние на статистику выбросов сверху и снизу и не позволяет средним 60% статистически скрывать неравенство, которое в противном случае очевидно в этой области. Эта мера используется для показателей развития человеческого потенциала Программы развития ООН. [4] [5] Соотношение 20:20, например, показывает, что в Японии и Швеции низкий разрыв в равенстве, где самые богатые 20% зарабатывают всего в 4 раза больше, чем самые бедные 20%, тогда как в Великобритании это соотношение составляет 7 раз, а в США — 8 раз. Некоторые полагают, что соотношение 20:20 является более полезным показателем, поскольку оно хорошо коррелирует с показателями человеческого развития и социальной стабильности, включая индекс благополучия детей, [6] индекс проблем здравоохранения и социальных проблем, [7] численность населения в тюрьмах, [8] физическое здоровье, [9] психическое здоровье [10] и многие другие. [11]
Соотношение Пальма

Коэффициент Пальмы определяется как отношение доли самых богатых 10% населения в валовом национальном доходе к доле самых бедных 40%. [12] Он основан на работе чилийского экономиста Габриэля Пальмы , который обнаружил, что доходы среднего класса почти всегда составляют около половины валового национального дохода, в то время как другая половина делится между самыми богатыми 10% и самыми бедными 40%, но доля этих двух групп значительно различается в разных странах. [13]
Коэффициент Пальмы учитывает повышенную чувствительность индекса Джини к изменениям в середине распределения и нечувствительность к изменениям в верхней и нижней части [14] и, следовательно, более точно отражает экономические последствия неравенства доходов для общества в целом. Пальма предположил, что распределительная политика в основном касается борьбы между богатыми и бедными и того, на чьей стороне средний класс. [13]
Коэффициент углерода Пальма, который выводится из коэффициента дохода Пальма и описывается как отношение общего объема выбросов 10% самых крупных эмитентов к общему объему выбросов 40% самых бедных, предлагается в качестве нового индикатора для информирования международного сообщества и широкой общественности о неравенстве распределения выбросов углерода среди отдельных лиц. Коэффициент рассчитывается как внутри стран, так и между ними с использованием эластичной связи между индивидуальными выбросами и доходами. Результаты показывают, что коэффициенты углерода Пальма в большинстве развивающихся стран, как правило, высоки, что подразумевает, что им следует больше концентрироваться на координации регионального и доходного неравенства и в первую очередь поощрять крупных эмитентов сокращать выбросы, чтобы одновременно повышать выбросы и справедливость доходов. Коэффициенты углерода Пальма в развитых странах сравнительно ниже; однако их более высокие исторические обязательства по потеплению указывают на то, что они значительно сокращают выбросы всех людей, чтобы систематически увеличивать национальные взносы на смягчение последствий. В глобальном масштабе текущий коэффициент углерода Пальма заметно выше, чем внутри любой страны, что указывает на чрезвычайно серьезное неравенство, когда индивидуальные выбросы рассматриваются за пределами территориальных границ. [15]
индекс Гувера
Индекс Гувера является самым простым для расчета показателем неравенства: это доля всех доходов, которую необходимо перераспределить для достижения состояния полного равенства.
В идеально равном мире не нужно было бы перераспределять ресурсы для достижения равного распределения: индекс Гувера равен 0. В мире, в котором весь доход получала бы только одна семья, почти 100% этого дохода пришлось бы перераспределять (т. е. забирать и отдавать другим семьям) для достижения равенства. Индекс Гувера тогда колеблется от 0 до 1 (0% и 100%), где 0 указывает на идеальное равенство, а 1 (100%) указывает на максимальное неравенство.
Оценка Галта
Оценка Галта — это простое отношение зарплаты генерального директора компании к зарплате среднего работника этой компании. Компания, которая платит своему генеральному директору во много раз больше, чем средний работник, будет иметь высокую оценку Галта.
Он назван в честь вымышленного персонажа Джона Галта из романа Айн Рэнд «Атлант расправил плечи» (1957).
Оценка рассчитывается с использованием общей компенсации генерального директора, включая заработную плату, бонусы, стоимость премий в виде акций и опционов на акции для сотрудников , а также компенсацию по плану поощрений, не связанную с акциями, и неквалифицированную отложенную компенсацию .
Коэффициент вариации
Коэффициент вариации (CV), используемый в качестве меры неравенства доходов, рассчитывается путем деления стандартного отклонения дохода (квадратного корня из дисперсии доходов) на среднее значение дохода. Поэтому коэффициент вариации будет ниже в странах с меньшим стандартным отклонением, что подразумевает более равномерное распределение доходов.
Он имеет преимущества в том, что он математически поддается обработке, а его квадрат разлагается на подгруппы, но он не ограничен сверху. Эта простая форма измерения не используется обычно в основном из-за двух ее существенных ограничений. Первое можно отнести к тому, что CV не имеет верхнего предела, в отличие от коэффициента Джини, что вызывает трудности с интерпретацией и сравнением. Во-вторых, поскольку среднее и стандартное отклонение могут сильно зависеть от аномальных пограничных значений, коэффициент не будет подходящим выбором меры неравенства доходов в случае ненормального распределения данных. [16]
По сравнению с коэффициентом Джини на практике, CV придает больший вес правому хвосту шкалы, делая ее чувствительной к богатым. Коэффициент вариации может быть подходящим выбором меры, если целью исследования является анализ концентрации богатства в верхней части распределения. [17] [18]
Дисперсия натурального логарифма дохода
Дисперсия логарифма дохода описывается как дисперсия, примененная к распределению логарифма дохода. [19] Эта инвариантная к масштабу мера относительного неравенства чувствительна к левому хвосту, что делает ее идеальной для использования при изучении уровней бедности половины населения с низким доходом (бедных). [16]
Доля заработной платы
Доля заработной платы — это отношение между компенсацией работникам и ВВП. Другими словами, это общая сумма доходов работников, деленная на национальный доход.
Мера бедности Сена
Показатель бедности Сена объединяет коэффициент Джини для людей, живущих за чертой бедности, с долей бедных и средним доходом тех, кто находится за чертой бедности. [20] Этот показатель был разработан лауреатом Нобелевской премии Амартией Сеном, но до сих пор не использовался в области гипотезы неравенства доходов. Хотя он был встречен с энтузиазмом, индекс бедности Сена не удовлетворяет ряду идеальных условий, например, он не удовлетворяет аксиоме переноса, он не является разложимым или согласованным по подгруппам. [21]
индекс Тейла
Как описано в разделе ниже, Theil-L — это дезэнтропия распределения доходов на человека, измеренная относительно максимальной энтропии (которая достигается при полном равенстве). (В альтернативной интерпретации Theil-L — это натуральный логарифм геометрического среднего отношения: (средний доход)/(доход i) по всем доходам. Соответствующий Atkinson(1) равен всего 1 минус геометрическое среднее отношение (доход i)/(средний доход) по распределению доходов.)
Поскольку трансферт между большим доходом и меньшим изменит соотношение меньшего дохода больше, чем соотношение большего дохода, этот индекс удовлетворяет принципу трансферта.
Индекс Тейла, равный 0, указывает на идеальное равенство. Индекс Тейла, равный 1, указывает на то, что энтропия распределения исследуемой системы почти подобна системе с распределением 82:18. [22] Это немного более неравномерно, чем неравенство в системе, к которой применяется « принцип Парето 80:20 ». [Примечание 2] Индекс Тейла можно преобразовать в индекс Аткинсона , который имеет диапазон от 0 до 1 (0% и 100%), где 0 указывает на идеальное равенство, а 1 (100%) указывает на максимальное неравенство. (См. Обобщенный индекс энтропии для преобразования.)
Индекс Тейла является мерой энтропии. Как и для любого распределения ресурсов и в отношении теории информации, «максимальная энтропия» возникает, когда получатели дохода не могут быть различены по своим ресурсам, т. е. когда существует полное равенство. В реальных обществах людей можно различить по их различным ресурсам, причем ресурсами являются доходы. Чем более они «различимы», тем ниже «реальная энтропия» системы, состоящей из дохода и получателей дохода. Также на основе теории информации разрыв между этими двумя энтропиями можно назвать « избыточностью ». [23] Он ведет себя как отрицательная энтропия .
Для индекса Тейла также использовался термин «энтропия Тейла». Это вызывало путаницу. В качестве примера Амартия Сен прокомментировал индекс Тейла: «Учитывая связь гибели с энтропией в контексте термодинамики, может потребоваться некоторое время, чтобы привыкнуть к энтропии как к чему-то хорошему». [24] Важно понимать, что увеличение индекса Тейла не указывает на увеличение энтропии, вместо этого оно указывает на увеличение избыточности (уменьшение энтропии).
Высокое неравенство приводит к высокой избыточности Тейла. Высокая избыточность означает низкую энтропию. Но это не обязательно означает, что очень высокое неравенство «хорошо», потому что очень низкая энтропия также может привести к взрывным процессам компенсации. Использование индекса Тейла также не обязательно означает, что очень низкое неравенство (низкая избыточность, высокая энтропия) «хорошо», потому что высокая энтропия связана с медленными, слабыми и неэффективными процессами распределения ресурсов.
Существует три варианта индекса Тейла. Применительно к распределению доходов первый индекс Тейла (Theil-L) относится к тому, как доход распределяется между получателями дохода, тогда как второй индекс Тейла (Theil-T) относится к тому, как получатели дохода распределяются между доходами.
Третий «симметризированный» индекс Тейла (Theil-S) — это арифметическое среднее двух предыдущих индексов. Формула третьего индекса Тейла имеет некоторое сходство с индексом Гувера (как объясняется в соответствующих статьях). Как и в случае индекса Гувера, симметризированный индекс Тейла не меняется при обмене доходов с получателями дохода. Как сгенерировать этот третий индекс Тейла с помощью вычислений в электронной таблице непосредственно из данных о распределении, показано ниже.
Важным свойством индекса Тейла, которое делает его применение популярным, является его разложение на межгрупповой и внутригрупповой компоненты. Например, индекс Тейла общего неравенства доходов может быть разложен на межрегиональные и внутрирегиональные компоненты неравенства, в то время как относительная доля, приписываемая межрегиональному компоненту, предполагает относительную важность пространственного измерения неравенства доходов. [25]
Сравнение индекса Тейла и индекса Гувера

Индекс Тейла указывает на распределительную избыточность системы, в которой доходы распределяются между получателями дохода в стохастическом процессе. Для сравнения, индекс Гувера указывает минимальный размер доли дохода общества, который должен быть перераспределен для достижения максимальной энтропии. Чтобы не превысить этот минимальный размер, потребуется идеально спланированное перераспределение. Таким образом, индекс Гувера является «нестохастическим» аналогом «стохастического» индекса Тейла.
Применение индекса Тейла к процессам распределения в реальном мире не означает, что эти процессы являются стохастическими: Тейл дает расстояние между упорядоченным распределением ресурсов в наблюдаемой системе и конечной стадией стохастического распределения ресурсов в закрытой системе. Аналогично, применение индекса Гувера не означает , что процессы распределения происходят в идеально спланированной экономике: индекс Гувера дает расстояние между распределением ресурсов в наблюдаемой системе и конечной стадией запланированного «выравнивания» распределения ресурсов. Для обоих индексов такое выравнивание служит только ссылкой, а не целью.
Для заданного распределения индекс Тейла может быть больше индекса Гувера или меньше индекса Гувера:
- Для высокого неравенства индекс Тейла больше индекса Гувера. Это означает, что для достижения равновесия (максимальной энтропии) в закрытой системе необходимо перераспределить больше ресурсов, чем в случае спланированного и оптимизированного процесса перераспределения, где необходимо перераспределять только необходимую минимальную долю ресурсов. Для открытой системы экспорт энтропии (импорт избыточности) позволит поддерживать динамику распределения, обусловленную высоким неравенством.
- Для низкого неравенства индекс Тейла меньше индекса Гувера. Здесь, на пути к достижению равновесия, запланированное и оптимизированное перераспределение ресурсов будет вносить больший вклад в динамику перераспределения, чем стохастическое перераспределение. Это также интуитивно понятно, поскольку низкое неравенство также ослабляет стремление к перераспределению ресурсов. Люди в такой системе могут терпеть или даже способствовать увеличению неравенства. Поскольку это было бы увеличением избыточности (уменьшением энтропии), избыточность должна была бы импортироваться в общество (энтропия должна была бы экспортироваться из) общества. В этом случае общество должно быть открытой системой. Чтобы увеличить избыточность в категории распределения общества как закрытой системы, энтропия должна быть экспортирована из подсистемы, работающей в этой экономической категории, в другие подсистемы с другими категориями энтропии в обществе. Например, может увеличиться социальная энтропия. Однако в реальном мире общества являются открытыми системами, но открытость ограничена возможностями обмена энтропией интерфейсов между обществом и средой этого общества. Для обществ с распределением ресурсов, которое по энтропии похоже на распределение ресурсов эталонного общества с разделением 73:27 (73% ресурсов принадлежат 27% населения и наоборот), [Примечание 3] точка, в которой индекс Гувера и индекс Тейла равны, находится на значении около 46% (0,46) для индекса Гувера и индекса Тейла.
индекс Аткинсона
Индекс Аткинсона (также известный как мера Аткинсона или мера неравенства Аткинсона) — это мера, полезная для определения того, какой конец распределения внес наибольший вклад в наблюдаемое неравенство.
Параметр ε Аткинсона часто называют «параметром неприятия неравенства», поскольку он регулирует чувствительность подразумеваемых потерь общественного благосостояния от неравенства к неравенству доходов, измеряемую некоторым соответствующим обобщенным индексом энтропии. Индекс Аткинсона определяется относительно соответствующей функции общественного благосостояния, где средний доход, умноженный на единицу за вычетом индекса Аткинсона, дает эквивалентный равномерно распределенный доход общественного благосостояния.
Индекс можно превратить в нормативную меру, назначив коэффициент ε для взвешивания доходов. Больший вес можно придать изменениям в заданной части распределения доходов, выбрав ε, уровень «неприятия неравенства», соответствующим образом. Индекс Аткинсона становится более чувствительным к изменениям в нижней части распределения доходов по мере увеличения ε. И наоборот, по мере того, как уровень неприятия неравенства падает (то есть, когда ε приближается к 0), индекс Аткинсона становится менее чувствительным к изменениям в нижней части распределения. Индекс Аткинсона ни для какого значения ε не является высокочувствительным к верхним доходам из-за общего ограничения, что ε неотрицательно.
Коэффициенты
Другой распространенный класс метрик — взять соотношение доходов двух разных групп, как правило, «выше по сравнению с ниже». Это сравнивает две части распределения доходов, а не распределение в целом; равенство между этими частями соответствует 1:1, в то время как чем более неравны части, тем больше соотношение. Эти статистические данные легко интерпретировать и сообщать, поскольку они относительны (эта группа населения зарабатывает вдвое больше, чем эта группа населения), но, поскольку они не попадают в абсолютную шкалу, не дают абсолютной меры неравенства.
Соотношение процентилей

Особенно часто сравнивают заданный процентиль с медианой, как на первой диаграмме здесь; сравните семизначное резюме , которое суммирует распределение по определенным процентилям. Хотя такие соотношения не отражают общий уровень неравенства в населении в целом, они дают представление о форме распределения доходов. Например, прилагаемый график показывает, что в период с 1967 по 2003 год соотношение доходов в США между медианой и 10-м и 20-м процентилями существенно не изменилось, в то время как соотношение между медианой и 80-м, 90-м и 95-м процентилями увеличилось. Это отражает то, что увеличение коэффициента Джини в США в этот период времени обусловлено приростом лиц с более высоким доходом (по отношению к медиане), а не потерями лиц с более низким доходом (по отношению к медиане).

Доля дохода
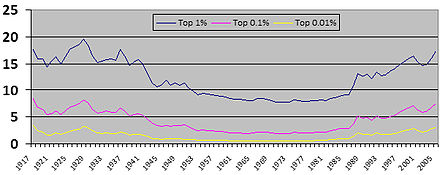
Связанный класс коэффициентов — «доля дохода», процент национального дохода, получаемый некоторой определенной самой богатой или самой бедной процентной группой населения.
Население, а кривая Лоренца (обсуждаемая в разделе Джини) отображает график совокупного дохода наименее обеспеченного населения x % для всех x от 0 до 100. Однако, комментируя данные, ее можно выразить как обратную величину, показывающую процент дохода самых богатых x %.
Важным и очевидным свойством кривой Лоренца является то, что если в стране А совокупная доля национального дохода, приходящаяся, скажем, на 1% беднейшего населения, выше, чем в стране В, то:
- Если кривые Лоренца двух стран не пересекаются, то кривая Лоренца страны А везде выше, чем кривая Лоренца страны В, что означает, что для любого значения X от 0 до 100 беднейшие X% населения имеют большую долю национального дохода в стране А, чем в стране В.
- Если кривые Лоренца двух стран пересекаются, то почти наверняка можно сказать, что на бедной стороне точки пересечения страна А имеет более высокую кривую Лоренца, что означает, что для любых беднейших X% населения до точки пересечения население страны А имеет большую долю национального дохода.
Когда неравенство наносит вред, оно наносит его в основном беднейшим слоям населения. В любом процентиле, упорядоченном по доходу, большая доля национального дохода означает больший полученный процент равной доли (средний национальный доход).
Таким образом, страна с большей совокупной долей национального дохода для 1% беднейшего населения будет иметь больший совокупный процент равной доли для X% беднейшего населения либо для каждого процентиля X, либо (если кривые Лоренца пересекаются) для процентилей на более бедной стороне точки пересечения.
Некоторые источники [ какие? ] сообщают о нескольких точках кривой Лоренца (совокупные доли национального дохода до нескольких процентилей).
Как упоминалось выше, соотношение доли дохода к размеру подгруппы населения соответствует соотношению среднего дохода подгруппы населения к среднему доходу.
Поскольку распределение доходов, как правило, имеет положительный перекос , среднее значение выше медианы, поэтому отношение к среднему значению ниже отношения к медиане. Это, в частности, используется для измерения той доли дохода, которая приходится на самых высокооплачиваемых лиц — 10%, 1%, 0,1%, 0,01%, а также на «100» самых высокооплачиваемых лиц и т. п.; в США 400 самых высокооплачиваемых лиц составляют 0,0002% от всех (2 из 1 000 000) — для изучения концентрации дохода — конденсации богатства или, скорее, конденсации дохода. Например, на диаграмме справа доля дохода самых высокооплачиваемых лиц в США была примерно постоянной с середины 1950-х до середины 1980-х годов, а затем увеличилась с середины 1980-х до 2000-х годов; это возросшее неравенство отразилось в коэффициенте Джини.
Например, в 2007 году на верхний дециль (10%) работников США приходилось 49,7% от общей заработной платы ( умноженное на дробь при равенстве), а на верхний 0,01% работников США приходилось 6% от общей заработной платы (умноженное на дробь при равенстве) [30] .
Подходы
Нормативный подход
Нормативная интерпретация неравенства через индексы неравенства означает, что существует связь между индексом неравенства и социально-оценочным порядком, определенным на основе доходов — доходов (номинальных или реальных) членов общества. Доходы обычно назначаются отдельным лицам, а не домохозяйствам, с использованием шкалы эквивалентности взрослых. [31]
Нормативный подход рассматривался Чарльзом Блэкорби, Уолтером Боссертом и Дэвидом Дональдсоном в работе «Измерение неравенства доходов: нормативный подход».
Статистический подход
Статистическая интерпретация неравенства основана на фискальных данных и параметре α из модели Парето (1895) как меры неравенства доходов . [32] Этот подход более подробно обсуждается в работе «Измерение неравенства доходов: статистический подход» Джованни М. Джорджи.
Расчеты в электронных таблицах
Коэффициент Джини, индекс Гувера и индекс Тейла, а также связанные с ними функции благосостояния [33] можно вычислить вместе в электронной таблице. [Примечание 5] Функции благосостояния служат альтернативами медианному доходу .
| Группа | Количество участников в группе | Доход на группу | Доход на душу населения | Относительное отклонение | Накопленный доход | Джини | Пылесос | Тейл |
|---|---|---|---|---|---|---|---|---|
| 1 | А 1 | Э 1 | Ē 1 = E 1 /A 1 | D 1 = E 1 /ΣE - A 1 /ΣA | К 1 = Э 1 | Г 1 = (2 * К 1 - Э 1 ) * А 1 | H 1 = абс(D 1 ) | Т 1 = ln(Ē 1 ) * D 1 |
| 2 | А 2 | Э 2 | Ē 2 = E 2 /A 2 | D 2 = E 2 /ΣE - A 2 /ΣA | К2 = Э2 + К1 | Г2 = ( 2 * К2 - Э2 ) * А2 | H 2 = абс(D 2 ) | Т 2 = ln(Ē 2 ) * D 2 |
| 3 | А 3 | Е 3 | Ē 3 = E 3 /A 3 | D 3 = E 3 /ΣE - A 3 /ΣA | К 3 = Э 3 + К 2 | Г 3 = (2 * К 3 - Э 3 ) * А 3 | H 3 = абс(D 3 ) | Т 3 = ln(Ē 3 ) * D 3 |
| 4 | А 4 | Е 4 | Ē 4 = Э 4 /А 4 | D 4 = E 4 /ΣE - A 4 /ΣA | К 4 = Э 4 + К 3 | С 4 = (2 * К 4 - Э 4 ) * А 4 | H 4 = абс(D 4 ) | Т 4 = ln(Ē 4 ) * D 4 |
| Итого | ΣА | ΣE | Ē = ΣE/ΣA | ΣG | ΣH | ΣТ | ||
| Меры неравенства | Джини = 1 - ΣG/ΣA/ΣE | Гувер = ΣH / 2 | Тейл = ΣT / 2 | |||||
| Функция благосостояния | W G = Ē * (1 - Джини) | W H = Ē * (1 - Гувер) | W T = Ē * (1 - Тейл) |
В таблице поля с желтым фоном используются для ввода данных. Из этих данных рассчитываются показатели неравенства, а также соответствующие функции благосостояния, которые отображаются в полях с зеленым фоном.
В приведенном здесь примере «индекс Тейла» означает среднее арифметическое индекса Тейла, вычисленного для распределения дохода внутри общества по отдельным лицам (или домохозяйствам) в этом обществе, и индекса Тейла, вычисленного для распределения отдельных лиц (или домохозяйств) в обществе по доходу этого общества. Разница между индексом Тейла и индексом Гувера заключается во взвешивании относительного отклонения D. Для индекса Гувера относительное отклонение D на группу взвешивается с собственным знаком. Для индекса Тейла относительное отклонение D на группу взвешивается с размером информации, предоставленным доходом на одного человека в этой группе.
Для расчета общество обычно делится на группы по уровню дохода. Часто бывает четыре или пять групп, состоящих из одинакового количества людей в каждой группе. В других случаях группы создаются на основе диапазонов доходов, что приводит к разному количеству людей в разных группах. В таблице выше показан расчет индексов неравенства для четырех групп. Для каждой группы указано количество людей (или домохозяйств) в группе A и общий доход в этой группе E.
Для вычисления коэффициента Джини необходимо отсортировать пары параметров A и E. (Для индекса Тейла и индекса Гувера сортировка не требуется.) A и E необходимо отсортировать таким образом, чтобы значения в столбце «Доход на душу населения» были выстроены в порядке возрастания.
Правильное использование
- При использовании показателей дохода необходимо четко указать, как следует определять доход. Должен ли он включать прирост капитала , вмененную арендную плату за жилье от владения домом и подарки? Если эти источники дохода или предполагаемые источники дохода (в случае « вмененной арендной платы ») игнорируются (как это часто бывает), как это может повлиять на анализ? Как следует обрабатывать неоплачиваемую работу (такую как родительский уход за детьми или самостоятельное приготовление пищи вместо найма повара для каждого приема пищи)? Богатство или потребление могут быть более подходящими мерами в некоторых ситуациях. Более широкие показатели качества жизни могут быть полезны.
- Сравнение показателей неравенства требует, чтобы сегментация сравниваемых групп (обществ и т. д.) на квинтили была схожей.
- Правильно различайте, является ли базовой единицей измерения домохозяйства или отдельные лица. Значение Джини для домохозяйств всегда ниже, чем для отдельных лиц из-за объединения доходов и внутрисемейных трансфертов. И в домохозяйствах разное количество членов. Метрики будут изменяться либо в сторону повышения, либо в сторону понижения в зависимости от того, какая единица измерения используется.
- Рассмотрим эффекты жизненного цикла. В большинстве западных обществ человек, как правило, начинает жизнь с небольшим или нулевым доходом, постепенно увеличивая доход примерно до 50 лет, после чего доход снижается, в конечном итоге становясь отрицательным. Это влияет на выводы, которые можно сделать из измеренного неравенства. Было подсчитано (AS Blinder в The Decomposition of Inequality , MIT press), что 30% измеренного неравенства доходов обусловлено неравенством, которое человек испытывает по мере прохождения различных этапов жизни.
- Уточните, следует ли использовать реальное или номинальное распределение доходов. Какое влияние окажет инфляция на абсолютные показатели? Ощущают ли некоторые группы (например, пенсионеры) влияние инфляции больше, чем другие?
- Делая выводы из измерений неравенства, подумайте, как нам следует распределять выгоды от государственных расходов? Как существование социальной защиты влияет на определение абсолютных показателей бедности? Поддерживают ли государственные программы некоторые группы доходов больше, чем другие?
- Метрики неравенства измеряют неравенство. Они не измеряют возможные причины неравенства доходов. Некоторые предполагаемые причины включают: эффекты жизненного цикла (возраст), унаследованные характеристики (IQ, талант), готовность рисковать (неприятие риска), выбор досуга/трудолюбия, унаследованное богатство, экономические обстоятельства, образование и обучение, дискриминация и несовершенство рынка.
- Показатели неравенства анонимны. Они игнорируют определенные эффекты мобильности доходов , в которых рассматривается идентичность «кто богат» и «кто беден». Например, в определенное время у Алисы может быть 10 долларов, а у Боба — 2 доллара. В какой-то момент времени у Боба может быть 10 долларов, а у Алисы — 2 доллара. Индекс неравенства будет одинаковым в обоих случаях и довольно высоким. Однако неравенство среднего будет равно нулю, поскольку средние активы Алисы и Боба равны (6 долларов). 8 долларов, которые перешли из рук в руки, являются мерой мобильности богатства, а среднее неравенство, как правило, выше, чем неравенство среднего.
Помня об этих моментах, можно понять проблемы, вызванные неправильным использованием мер неравенства. Однако они не делают коэффициенты неравенства недействительными. Если меры неравенства вычисляются хорошо объясненным и последовательным образом, они могут стать хорошим инструментом для количественного сравнения неравенств.
Неравенство, рост и прогресс
Данные из широкого круга недавних академических исследований показывают, что существует нелинейная связь между неравенством доходов и темпами роста и инвестиций. Очень высокое неравенство замедляет рост; умеренное неравенство стимулирует рост. Исследования расходятся во мнениях относительно влияния очень низкого неравенства.
Роберт Дж. Барро из Гарвардского университета в своем исследовании «Неравенство и рост в группе стран» обнаружил, что более высокое неравенство имеет тенденцию замедлять рост в бедных странах и стимулировать рост в хорошо развитых регионах. [34] Подчеркивая необходимость таких инициатив, как Цель 10 в области устойчивого развития Организации Объединенных Наций , направленных на сокращение неравенства. [35] По словам Пак Хунг Мо, неравенство доходов оказывает существенное негативное влияние на темпы роста ВВП . В своей работе «Неравенство доходов и экономический рост» они обнаружили, что наиболее важным является канал передачи, а наименее важным — канал человеческого капитала. Однако прямое влияние неравенства доходов на темпы роста производительности составляет более 55 процентов от его общего совокупного эффекта. Это указывает на то, что влияние неравенства доходов на экономический рост гораздо сложнее, чем мы воспринимали или моделировали. [36]
В своем исследовании для Всемирного института исследований экономики развития Джованни Андреа Корниа и Джулиус Корт (2001) пришли к несколько иным выводам. [37] [38] Поэтому авторы рекомендуют придерживаться умеренности также в отношении распределения богатства и, в частности, избегать крайностей. Как очень высокий эгалитаризм, так и очень высокое неравенство вызывают медленный рост. Учитывая неравенство в экономически развитых странах, государственная политика должна быть нацелена на «эффективный диапазон неравенства». Авторы утверждают, что такой диапазон эффективности примерно лежит между значениями коэффициентов Джини 0,25 (неравенство, близкое к наименее неравным европейским странам) и 0,40 (близкое к уровню неравенства в США.
Согласно работе «Неравенство возможностей, неравенство доходов и экономический рост», связь между неравенством доходов и экономическим ростом опосредована уровнем равенства возможностей, определяемым межпоколенческой мобильностью. После ряда недавно разработанных международно сопоставимых мер межпоколенческой мобильности они подтвердили, что негативное влияние неравенства доходов на рост увеличивается по мере снижения межпоколенческой мобильности. Результаты подразумевают, что исключение межпоколенческой мобильности приводит к неправильной спецификации, что объясняет, почему эмпирическая литература по неравенству доходов и росту была столь неубедительной. [39]
Другой исследователь показал, что на совершенных рынках неравенство не влияет на рост. [40]
Точная форма кривой неравенства-роста, очевидно, различается в разных странах в зависимости от их обеспеченности ресурсами, истории, сохраняющегося уровня абсолютной бедности и имеющегося фонда социальных программ, а также от распределения физического и человеческого капитала.
Смотрите также
- Список стран по уровню равенства доходов
- Список стран по уровню благосостояния
- Неравенство доходов в Соединенных Штатах
- Дефицит дохода
- Международное неравенство
- кривая Кузнеца
- Порог бедности
- Социоэкономика
- Цели устойчивого развития
- « Богатые становятся еще богаче, а бедные — еще беднее »
- Распределительная справедливость – политический идеал, направленный на большее равенство доходов
- Индекс разнообразия
- Кривая Великого Гэтсби
- Индекс развития человеческого потенциала
- Индекс костюмов
- индекс Джини
- кривая Лоренца
- Кривая Слона
Примечания
- ^ О бедности см. показатели FGT .
- ^ Индекс Тейла 0,5 характеризует системы, близкие к распределению 74:26. Распределение 92:8 даст индекс Тейла 2, а 98:2 даст 4. Некоторые особые наблюдения: Для распределения 80:20 (принцип Парето) индекс Тейла равен 0,83. Для 73:27 индекс Тейла и индекс Гувера идентичны: оба равны 0,46. Для 62:38 разница между индексом Тейла (представляющим стохастическое распределение) и индексом Гувера (представляющим идеально спланированное распределение) достигает минимума в −0,12.
- ^ В таких обществах, которые разделены на два так называемых «а-фрактиля», индекс Гувера и коэффициент Джини всегда близки.
- ^ Различия между данными переписи и данными Службы внутренних доходов легче всего увидеть в 95-м процентиле, присутствующем в обоих наборах данных. Более подробную информацию см. в файле справки для данных "incomeInequality" в пакете Ecdat, доступном в Comprehensive R Archive Network (CRAN; см. r-project.org).
- ^ В качестве альтернативы вычислениям в электронных таблицах можно использовать скрипт Python.
Ссылки
- ^ "Survey Unit – surveyunit". Worldbank.org . Получено 8 сентября 2018 г. .
- ^ "Basics and Completely Decomposable Groups", Almost Completely Decomposable Groups , CRC Press, стр. 37–72, 2000-03-09, doi :10.1201/9781482287486-8, ISBN 978-0-429-07843-9, получено 2021-04-30
- ^ "Рисунок 5.8. Коэффициенты Джини различных показателей неравенства между провинциями". doi :10.1787/778454437583 . Получено 2021-04-30 .
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) - ^ «Notes on Statistical Sources and Methods – The Equality Trust». Equalitytrust.org.uk . Архивировано из оригинала 16 января 2014 года . Получено 8 сентября 2018 года .
- ^ Эконометрика панельных данных: теоретические вклады и эмпирические приложения под редакцией Бади Хани Балтаг
- ^ "Радиография". Br Med J . 2 (4157): 321. 7 сентября 1940 г. doi :10.1136/bmj.2.4157.321-a. S2CID 214960331 . Получено 8 сентября 2018 г. – через www.bmj.com.
- ^ "Экономическое неравенство вредно для вашего здоровья". Архивировано из оригинала 2013-05-25 . Получено 2013-05-18 .
- ^ "Тюремное заключение – The Equality Trust". Equalitytrust.org.uk . Получено 8 сентября 2018 г. .
- ^ "Physical Health – The Equality Trust". Equalitytrust.org.uk . Получено 8 сентября 2018 г. .
- ^ "Психическое здоровье – The Equality Trust". Equalitytrust.org.uk . Получено 8 сентября 2018 г. .
- ^ "Внешние исследования – Страница 2 – The Equality Trust". Equalitytrust.org.uk . Получено 8 сентября 2018 г. .
- ^ Алекс Кобэм; Энди Самнер (15 марта 2013 г.). «Возвращение индекса Джини в бутылку? «Пальма» как показатель неравенства, значимый для политики» (PDF) . King's International Development Institute . King's College London. Архивировано из оригинала (PDF) 23 апреля 2013 г. . Получено 14 января 2019 г. .
- ^ ab Palma, José Gabriel (январь 2011 г.). «Однородные середины против неоднородных хвостов и конец «перевернутой U»: все дело в доле богатых» (PDF) . Cambridge Working Papers in Economics (CWPE) 1111. Cambridge University . Получено 19 марта 2013 г.
- ^ Аткинсон, Энтони (1970). «Об измерении неравенства» (PDF) . Журнал экономической теории . 2 (3): 244–63. doi :10.1016/0022-0531(70)90039-6 . Получено 19 марта 2013 г. .
- ^ Пан, Сюньчжан; Ван, Хайлинь; Ван, Цзывэй; Линь, Лу; Чжан, Ци; Чжэн, Синьчжу; Чэнь, Вэньин (декабрь 2019 г.). «Соотношение углерода и пальмы: новый показатель для измерения неравенства распределения выбросов углерода среди людей». Журнал чистого производства . 241 : 118418. doi : 10.1016/j.jclepro.2019.118418. ISSN 0959-6526. S2CID 203452007.
- ^ ab Трапезникова, Ия (2019-07-17). "Измерение неравенства доходов". IZA World of Labor . doi : 10.15185/izawol.462 .
- ^ Рено, Б.; Буда, М.; Льюис, Б. Д.; Пуйоль, Дж. Ф. (1975-09-15). «Влияние 5,6-дигидрокситриптамина на активность тирозингидроксилазы в центральных катехоламинергических нейронах крысы». Биохимическая фармакология . 24 (18): 1739–1742. doi :10.1016/0006-2952(75)90018-0. ISSN 0006-2952. PMID 17.
- ^ Рис, ММ; Дейтрих, РА; Фон Вартбург, ДжП (1975-10-15). «Ингибирование изоферментов альдегидредуктазы в мозге человека и крысы». Биохимическая фармакология . 24 (20): 1865–1869. doi :10.1016/0006-2952(75)90405-0. ISSN 0006-2952. PMID 18.
- ^ Фостер, Джеймс Э.; Ок, Эфе А. (июль 1999 г.). «Доминирование Лоренца и дисперсия логарифмов». Econometrica . 67 (4): 901–907. doi :10.1111/1468-0262.00057. ISSN 0012-9682.
- ^ Fahnestock, SR (1975-12-02). «Доказательства участия 50S рибосомального белка в нескольких активных сайтах». Биохимия . 14 (24): 5321–5327. doi :10.1021/bi00695a016. ISSN 0006-2960. PMID 52.
- ^ Шоррокс, Энтони Ф. (сентябрь 1995 г.). «Пересмотр индекса бедности Сена». Econometrica . 63 (5): 1225–1230. doi :10.2307/2171728. JSTOR 2171728.
- ^ "Онлайн-калькулятор: неравенство". Poorcity.richcity.org . Получено 8 сентября 2018 г. .
- ^ ISO/IEC DIS 2382-16:1996 ( Теория информации )
- ↑ стр. 35, глава 2.11 в книге Амартия Сен и Джеймс Э. Фостер: Об экономическом неравенстве , Oxford University Press, 1996 (скрипт Python, архивированный 19 июля 2011 г. на Wayback Machine для выбора формул в книге).
- ^ Новотны, Дж. (2007). «Об измерении регионального неравенства: имеет ли значение пространственное измерение неравенства доходов?» (PDF) . Annals of Regional Science . 41, 3 (3): 563–80. doi :10.1007/s00168-007-0113-y. S2CID 51753883.
- ^ "Таблица F-1. Пределы доходов для каждого пятого и верхних 5 процентов семей (все расы): 1947 по 2010 год". Текущее обследование населения, ежегодные социальные и экономические дополнения . Бюро переписи населения США . Получено 24.01.2012 .
Медиана вычисляется как геометрическое среднее 20-го и 40-го процентилей.
- ^ Пикетти, Томас ; Саез, Эммануэль , «Неравенство доходов в Соединенных Штатах, 1913–2002», в Аткинсон, AB; Пикетти, Томас (ред.), Максимальные доходы в течение двадцатого века: контраст между континентальными европейскими и англоязычными странами , получено 2012-02-08
- ^ Саез, Э. и Пикетти, Т. (2003). «Неравенство доходов в Соединенных Штатах: 1913–1998». Quarterly Journal of Economics , 118(1), 1–39.
- ^ "Saez, E. (октябрь 2007 г.). Таблица A1: Верхние квантили распределения доходов (исключая прирост капитала) в США, 1913–2005 гг.". Elsa.berkeley.edu . Получено 17.01.2008 .
- ^ «Стать богаче: эволюция самых высоких доходов в Соединенных Штатах», обновлено в августе 2009 г., Эммануэль Саез, резюме работы для широкой общественности.
- ^ Чарльз., Блэкорби (1999). Измерение неравенства доходов: нормативный подход. [sn] OCLC 848679839.
- ^ Мария., Джорджи, Джованни (1999). Измерение неравенства доходов: статистический подход. [sn] OCLC 848679881.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Джеймс Э. Фостер и Амартия Сен, 1997, Об экономическом неравенстве, расширенное издание с существенным приложением , ISBN 0-19-828193-5 . Для вычисления функции благосостояния Сен привел пример с использованием коэффициента Джини, тогда как Фостер использовал меру энтропии. Индекс Тейла является такой мерой энтропии.
- ^ "Неравенство и рост в группе стран" (PDF) . Scholar.harvard.edu . Получено 8 сентября 2018 г. .
- ^ "Goal 10 tasks". ПРООН . Архивировано из оригинала 2020-11-27 . Получено 2020-09-23 .
- ^ Мо, Пак Хунг (2000). «Неравенство доходов и экономический рост». Международный обзор социальных наук . 53 (3): 293–315. doi :10.1111/1467-6435.00122.
- ^ «Неравенство, рост и бедность в эпоху либерализации и глобализации». UNU-WIDER . 2015-08-18 . Получено 2019-05-25 .
- ^ "UNU-WIDER : Publications" (PDF) . UNU-WIDER . Архивировано из оригинала (PDF) 14 июля 2020 г. . Получено 8 сентября 2018 г. .
- ^ Айяр, Шехар; Эбеке, Кристиан (декабрь 2020 г.). «Неравенство возможностей, неравенство доходов и экономический рост». Мировое развитие . 136 : 105115. doi : 10.1016/j.worlddev.2020.105115. ISSN 0305-750X. S2CID 224891145.
- ^ Вольфганг Киттерер: Mehr Wachstum durch Umverteilung? Архивировано 27 сентября 2007 г. в Wayback Machine (Больший рост за счет перераспределения?) , 2006 г.
Литература
- AB Atkinson и F. Bourguignon, ред. (2000). Справочник по распределению доходов , т. 1. Elsevier.оглавление
- _____, « Международная энциклопедия социальных и поведенческих наук» (2001), стр. 7265–7271. Аннотация.
- Йорам Амиель (автор), Фрэнк А. Коуэлл: Размышления о неравенстве: личное суждение и распределение доходов , 2000
- Филип Б. Коултер: Измерение неравенства , 1989
Внешние ссылки
- Трэвис Хейл, Проект неравенства Техасского университета: Теоретические основы популярных мер неравенства; онлайн-вычисление примеров: 1A, 1B
- Сэмюэл Мюррей Матесон: Меры распределительной справедливости для выбора устойчивого проекта, 1997 г.
- Исследование доходов в Люксембурге проводит сравнительное исследование неравенства доходов
- Две Америки: одна богатая, другая бедная? Понимание неравенства доходов в Соединенных Штатах
- Действительно ли неравенство доходов в США возросло?
- Сайт, посвященный теме неравенства доходов
- WIID – База данных о неравенстве доходов в мире, Всемирный институт исследований экономики развития Университета ООН
- Программное обеспечение:
- Онлайн-калькулятор вычисляет коэффициент Джини, строит кривую Лоренца и вычисляет множество других показателей концентрации для любого набора данных.
- Онлайн-калькулятор: Онлайн (пример для обработки данных из Таблицы HINC-06 [ постоянная неработающая ссылка ] , Бюро переписи населения США, 2007: Распределение доходов домохозяйств с доходом до 250 000 долларов США или более) и загружаемые скрипты ( Python и Lua ) для неравенств Аткинсона, Джини и Гувера
- Скрипт Python, архив 2011-07-10 на Wayback Machine, с использованием формул из книги Амартии Сена «Об экономическом неравенстве»
- Пользователи программного обеспечения для анализа данных R могут установить пакет ineq, который позволяет вычислять различные индексы неравенства, включая Джини, Аткинсона и Тейла.
- Пакет неравенства MATLAB Архивировано 2008-10-04 на Wayback Machine , включая код для вычисления индексов Джини, Аткинсона, Тейла и для построения кривой Лоренца. Доступно много примеров.








