последовательность Падована
Последовательность целых чисел

В теории чисел последовательность Падована — это последовательность целых чисел P ( n ), определяемая [1] начальными значениями

П ( 0 ) = П ( 1 ) = П ( 2 ) = 1 , {\displaystyle P(0)=P(1)=P(2)=1,}

и рекуррентное соотношение

П ( н ) = П ( н − 2 ) + П ( н − 3 ) . {\displaystyle P(n)=P(n-2)+P(n-3).}

Первые несколько значений P ( n ) равны

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, ... (последовательность A000931 в OEIS )

Простое число Падована — это число Падована, которое является простым . Первые простые числа Падована:

2, 3, 5, 7, 37, 151, 3329, 23833, 13091204281, 3093215881333057, 1363005552434666078217421284621279933627102780881053358473, 1558877695141608507751098941899265975115403618621811951868598809164180630185566719, ... (последовательность A100891 в OEIS ).
Спираль из равносторонних треугольников с длинами сторон, которые следуют последовательности Падована.

Последовательность Падована названа в честь Ричарда Падована , который приписал ее открытие голландскому архитектору Хансу ван дер Лаану в своем эссе 1994 года Dom. Hans van der Laan: Modern Primitive . [2] Последовательность была описана Яном Стюартом в его колонке Scientific American Mathematical Recreations в июне 1996 года. [3] Он также пишет о ней в одной из своих книг «Math Hysteria: Fun Games With Mathematics». [4]

Вышеприведенное определение дано Яном Стюартом и MathWorld . Другие источники могут начинать последовательность в другом месте, и в этом случае некоторые тождества в этой статье должны быть скорректированы с соответствующими смещениями.

Рекуррентные соотношения

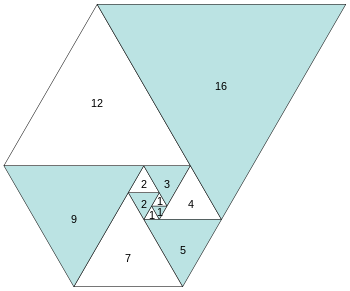
В спирали каждый треугольник имеет общую сторону с двумя другими, что наглядно доказывает, что последовательность Падована также удовлетворяет рекуррентному соотношению.

П ( н ) = П ( н − 1 ) + П ( н − 5 ) {\displaystyle P(n)=P(n-1)+P(n-5)}

Исходя из этого, определяющего повторения и других повторений по мере их обнаружения, можно создать бесконечное количество дальнейших повторений, многократно заменяя на П ( м ) {\displaystyle P(м)} П ( м − 2 ) + П ( м − 3 ) {\displaystyle P(м-2)+P(м-3)}

Последовательность Перрена удовлетворяет тем же рекуррентным соотношениям, что и последовательность Падована, хотя имеет другие начальные значения.

Последовательность Перрена может быть получена из последовательности Падована по следующей формуле:

П е г г я н ( н ) = П ( н + 1 ) + П ( н − 10 ) . {\ displaystyle \ mathrm {Перрин} (n) = P (n + 1) + P (n-10). \,}

Расширение до отрицательных параметров

Как и в случае любой последовательности, определяемой рекуррентным соотношением, числа Падована P ( m ) при m < 0 можно определить, переписав рекуррентное соотношение как

П ( м ) = П ( м + 3 ) − П ( м + 1 ) , {\displaystyle P(м)=P(м+3)-P(м+1),}

Начиная с m = −1 и двигаясь в обратном направлении, мы расширяем P ( m ) до отрицательных индексов:

П −20П −19П −18П −17П −16П −15П −14П −13П −12П −11П −10П −9П −8П −7П −6П −5П −4П −3П −2П −1П 0П 1П 2
7−740−34−311−22−101−110010111

Суммы слагаемых

Сумма первых n членов последовательности Падована на 2 меньше P ( n  + 5), т.е.

∑ м = 0 н П ( м ) = П ( н + 5 ) − 2. {\displaystyle \sum _{m=0}^{n}P(m)=P(n+5)-2.}

Суммы чередующихся членов, суммы каждого третьего члена и суммы каждого пятого члена также связаны с другими членами последовательности:

∑ м = 0 н П ( 2 м ) = П ( 2 н + 3 ) − 1 {\displaystyle \sum _{m=0}^{n}P(2m)=P(2n+3)-1} OEIS : A077855
∑ м = 0 н П ( 2 м + 1 ) = П ( 2 н + 4 ) − 1 {\displaystyle \sum _{m=0}^{n}P(2m+1)=P(2n+4)-1}
∑ м = 0 н П ( 3 м ) = П ( 3 н + 2 ) {\displaystyle \sum _{m=0}^{n}P(3m)=P(3n+2)} OEIS : A034943
∑ м = 0 н П ( 3 м + 1 ) = П ( 3 н + 3 ) − 1 {\displaystyle \sum _{m=0}^{n}P(3m+1)=P(3n+3)-1}
∑ м = 0 н П ( 3 м + 2 ) = П ( 3 н + 4 ) − 1 {\displaystyle \sum _{m=0}^{n}P(3m+2)=P(3n+4)-1}
∑ м = 0 н П ( 5 м ) = П ( 5 н + 1 ) . {\displaystyle \sum _{m=0}^{n}P(5m)=P(5n+1).} OEIS : A012772

Суммы, включающие произведения членов последовательности Падована, удовлетворяют следующим тождествам:

∑ м = 0 н П ( м ) 2 = П ( н + 2 ) 2 − П ( н − 1 ) 2 − П ( н − 3 ) 2 {\displaystyle \sum _{m=0}^{n}P(m)^{2}=P(n+2)^{2}-P(n-1)^{2}-P(n-3)^{2}}
∑ м = 0 н П ( м ) 2 П ( м + 1 ) = П ( н ) П ( н + 1 ) П ( н + 2 ) {\displaystyle \sum _{m=0}^{n}P(m)^{2}P(m+1)=P(n)P(n+1)P(n+2)}
∑ м = 0 н П ( м ) П ( м + 2 ) = П ( н + 2 ) П ( н + 3 ) − 1. {\displaystyle \sum _{m=0}^{n}P(m)P(m+2)=P(n+2)P(n+3)-1.}

Другие идентичности

Последовательность Падована также удовлетворяет тождеству

П ( н ) 2 − П ( н + 1 ) П ( н − 1 ) = П ( − н − 7 ) . {\displaystyle P(n)^{2}-P(n+1)P(n-1)=P(-n-7).\,}

Последовательность Падована связана с суммами биномиальных коэффициентов следующим тождеством:

П ( к − 2 ) = ∑ 2 м + н = к ( м н ) = ∑ м = ⌈ к / 3 ⌉ ⌊ к / 2 ⌋ ( м к − 2 м ) . {\displaystyle P(k-2)=\sum _{2m+n=k}{m \choose n}=\sum _{m=\lceil k/3\rceil }^{\lfloor k/2\rfloor }{m \choose k-2m}.}

Например, для k = 12 значения для пары ( m ,  n ) при 2m  +  n = 12, которые дают ненулевые биномиальные коэффициенты, равны (6, 0), (5, 2) и (4, 4), а также:

( 6 0 ) + ( 5 2 ) + ( 4 4 ) = 1 + 10 + 1 = 12 = П ( 10 ) . {\displaystyle {6 \выбрать 0}+{5 \выбрать 2}+{4 \выбрать 4}=1+10+1=12=P(10).\,}

Формула типа Бине

Треугольники со сторонами в отношении 1/ ρ образуют замкнутую спираль

Последовательность чисел Падована можно записать в терминах степеней корней уравнения [ 1]

х 3 − х − 1 = 0. {\displaystyle x^{3}-x-1=0.\,}

Это уравнение имеет 3 корня: один действительный корень p (известный как пластическое отношение ) и два комплексно-сопряженных корня q и r . [5] Учитывая эти три корня, последовательность Падована можно выразить формулой, включающей p , q и r  :

П ( н ) = а п н + б д н + с г н {\displaystyle P(n)=ap^{n}+bq^{n}+cr^{n}}

где a , b и c — константы. [1]

Поскольку абсолютные значения комплексных корней q и r меньше 1 (и, следовательно, p является числом Пизо–Виджаярагхавана ), степени этих корней стремятся к 0 при больших n и стремятся к нулю. П ( н ) − а п н {\displaystyle P(n)-ap^{n}}

Для всех P ( n ) — ближайшее к целое число . Действительно, — это значение константы a выше, тогда как b и c получаются путем замены p на q и r соответственно. н ≥ 0 {\displaystyle n\geq 0} п 5 2 п + 3 п н {\displaystyle {\frac {p^{5}}{2p+3}}p^{n}} п 5 2 п + 3 {\displaystyle {\frac {p^{5}}{2p+3}}}

Отношение последовательных членов в последовательности Падована приближается к p , что имеет значение приблизительно 1,324718. Эта константа имеет такое же отношение к последовательности Падована и последовательности Перрена , как золотое сечение к последовательности Фибоначчи .

Комбинаторные интерпретации

  • P ( n ) — это число способов записи n  + 2 в виде упорядоченной суммы, в которой каждый член равен либо 2, либо 3 (т.е. число композиций n  + 2, в которых каждый член равен либо 2, либо 3). Например, P (6) = 4, и существует 4 способа записи 8 в виде упорядоченной суммы двоек и троек :
2 + 2 + 2 + 2 ; 2 + 3 + 3 ; 3 + 2 + 3 ; 3 + 3 + 2
  • Число способов записи n в виде упорядоченной суммы, в которой ни один член не равен 2, равно P (2 n  − 2). Например, P (6) = 4, и существует 4 способа записи 4 в виде упорядоченной суммы, в которой ни один член не равен 2:
4 ; 1 + 3 ; 3 + 1; 1 + 1 + 1 + 1
  • Число способов записи n в виде палиндромной упорядоченной суммы, в которой ни один член не равен 2, равно P ( n ). Например, P (6) = 4, и существует 4 способа записи 6 в виде палиндромной упорядоченной суммы, в которой ни один член не равен 2:
6 ; 3 + 3; 1 + 4 + 1 ; 1 + 1 + 1 + 1 + 1 + 1
  • Число способов записи n в виде упорядоченной суммы, в которой каждый член нечетный и больше 1, равно P ( n  − 5). Например, P (6) = 4, и существует 4 способа записи 11 в виде упорядоченной суммы, в которой каждый член нечетный и больше 1:
11 ; 5 + 3 + 3 ; 3 + 5 + 3 ; 3 + 3 + 5
  • Число способов записи n в виде упорядоченной суммы, в которой каждый член сравним с 2 mod 3, равно P ( n  − 4). Например, P (6) = 4, и существует 4 способа записи 10 в виде упорядоченной суммы, в которой каждый член сравним с 2 mod 3:
8 + 2 ; 2 + 8 ; 5 + 5 ; 2 + 2 + 2 + 2 + 2

Производящая функция

Производящая функция последовательности Падована имеет вид

Г ( П ( н ) ; х ) = 1 + х 1 − х 2 − х 3 . {\displaystyle G(P(n);x)={\frac {1+x}{1-x^{2}-x^{3}}}.}

Это можно использовать для доказательства тождеств, включающих произведения последовательности Падована с геометрическими терминами , такими как:

∑ н = 0 ∞ П ( н ) 2 н = 12 5 . {\displaystyle \sum _{n=0}^{\infty }{\frac {P(n)}{2^{n}}}={\frac {12}{5}}.}
∑ н = 0 ∞ П ( н ) α н = α 2 ( α + 1 ) α 3 − α − 1 . {\displaystyle \sum _{n=0}^{\infty }{\frac {P(n)}{\alpha ^{n}}}={\frac {\alpha ^{2}(\alpha +1 )}{\alpha ^{3}-\alpha -1}}.}

Обобщения

Аналогично числам Фибоначчи , которые можно обобщить до набора многочленов, называемых многочленами Фибоначчи , последовательность чисел Падована можно обобщить, получив многочлены Падована .

L-система Padovan

Если мы определим следующую простую грамматику:

переменные  : ABC
константы  : нет
начало  : А
правила  : (A → B), (B → C), (C → AB)

то эта система Линденмайера или L-система производит следующую последовательность строк:

n = 0 : А
n = 1 : В
n = 2 : С
n = 3 : АВ
n = 4 : БК
n = 5 : КАБ
n = 6 : АБВГ
n = 7 : BCCAB
n = 8 : КАБАББК

и если мы посчитаем длину каждой строки, то получим числа Падована:

1, 1, 1, 2, 2, 3, 4, 5, ...

Кроме того, если вы подсчитаете количество букв A , B и C в каждой строке, то для n -й строки у вас будет P ( n  − 5) букв A , P ( n  − 3) букв B и P ( n  − 4) букв C. Количество пар BB и пар CC также является числами Падована.

Кубовидная спираль

Спираль может быть образована путем соединения углов набора трехмерных кубоидов . Это спираль кубоида Падована . Последовательные стороны этой спирали имеют длины, которые являются числами Падована, умноженными на квадратный корень из 2 .

Треугольник Паскаля

Эрв Уилсон в своей статье «Весы горы Меру» [6] наблюдал определенные диагонали в треугольнике Паскаля (см. диаграмму) и нарисовал их на бумаге в 1993 году. Числа Падована были открыты в 1994 году. Пол Барри (2004) заметил, что эти диагонали генерируют последовательность Падована путем суммирования диагональных чисел. [7]

Ссылки

  1. ^ abc Вайсстейн, Эрик В. "Последовательность Падована". MathWorld ..
  2. ^ Ричард Падован. Дом Ханс ван дер Лаан: современный примитив : Architectura & Natura Press, ISBN 9789071570407 . 
  3. ↑ Ян Стюарт, Рассказы о забытом числе, Scientific American , № 6, июнь 1996 г., стр. 92-93.
  4. ^ Ян Стюарт (2004), Математическая истерия: развлечения и игры с математикой , Oxford University Press, стр. 87, ISBN 978-0-19-861336-7.
  5. ^ Ричард Падован, «Дом Ханс Ван дер Лаан и пластиковое число», стр. 181-193 в Nexus IV: Архитектура и математика, ред. Ким Уильямс и Хосе Франциско Родригес, Fucecchio (Флоренция): Kim Williams Books, 2002.
  6. ^ Эрв Уилсон (1993), Весы горы Меру
  7. ^ Sloane, N. J. A. (ред.). "Последовательность A000931". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.См. формулу, приписываемую Полу Барри, 6 июля 2004 г.
  • Ян Стюарт, Руководство по компьютерному знакомству (обратная связь), Scientific American, т. 275, № 5, ноябрь 1996 г., стр. 118.
  • Последовательность OEIS A000931 (последовательность Падована)
  • Калькулятор последовательности Padovan
Взято с "https://en.wikipedia.org/w/index.php?title=Padovan_sequence&oldid=1245185289"