Ортоцентрическая система
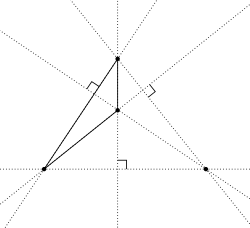
В геометрии ортоцентрическая система — это набор из четырёх точек на плоскости , одна из которых является ортоцентром треугольника , образованного тремя другими. Эквивалентно, прямые, проходящие через непересекающиеся пары среди точек, перпендикулярны , а четыре окружности, проходящие через любые три из четырёх точек, имеют одинаковый радиус. [1]
Если четыре точки образуют ортоцентрическую систему, то каждая из четырех точек является ортоцентром трех других. Все эти четыре возможных треугольника будут иметь одну и ту же девятиточечную окружность . Следовательно, все эти четыре возможных треугольника должны иметь описанные окружности с одинаковым радиусом описанной окружности .
Обычный девятиточечный круг

Центр этой общей девятиточечной окружности лежит в центроиде четырех ортоцентрических точек. Радиус общей девятиточечной окружности — это расстояние от центра девяти точек до середины любого из шести соединителей, соединяющих любую пару ортоцентрических точек, через которые проходит общая девятиточечная окружность. Девятиточечная окружность также проходит через три ортогональных пересечения в основаниях высот четырех возможных треугольников.
Этот общий центр из девяти точек лежит в середине соединителя, который соединяет любую ортоцентрическую точку с центром описанной окружности треугольника, образованного тремя другими ортоцентрическими точками.
Общая девятитрассовая окружность касается всех 16 вписанных и вневписанных окружностей четырех треугольников, вершины которых образуют ортоцентрическую систему. [2]
Общий ортоцентрический треугольник, его инцентр и его вневписанные центры
Если шесть соединителей, которые соединяют любую пару ортоцентрических точек, продлить до шести линий, которые пересекаются друг с другом, они образуют семь точек пересечения. Четыре из этих точек являются исходными ортоцентрическими точками, а дополнительные три точки являются ортогональными пересечениями у подножий высот . Объединение этих трех ортогональных точек в треугольник образует ортоцентрический треугольник , который является общим для всех четырех возможных треугольников, образованных из четырех ортоцентрических точек, взятых по три за раз.
Инцентр этого общего ортоцентрического треугольника должен быть одной из исходных четырех ортоцентрических точек. Более того, три оставшиеся точки становятся вневписанными центрами этого общего ортоцентрического треугольника. Ортоцентрическая точка, которая становится вписанным центром ортоцентрического треугольника, — это ортоцентрическая точка, ближайшая к общему девятиточечному центру. Эта связь между ортоцентрическим треугольником и исходными четырьмя ортоцентрическими точками напрямую приводит к тому факту, что вписанный и вневписанный центры референц-треугольника образуют ортоцентрическую систему. [3]
Обычно принято отличать одну из ортоцентрических точек от других, в частности ту, которая является инцентром ортоцентрического треугольника; она обозначается H как ортоцентр внешних трех ортоцентрических точек, которые выбраны в качестве опорного треугольника △ ABC . В этой нормализованной конфигурации точка H всегда будет лежать внутри треугольника △ ABC , и все углы треугольника △ ABC будут острыми. Четыре возможных треугольника, упомянутые выше, тогда являются треугольниками △ ABC , △ ABH , △ ACH , △ BCH . Шесть упомянутых выше соединителей - это AB , AC , BC , AH , BH , CH . Семь упомянутых выше пересечений - это A, B, C, H (исходные ортоцентрические точки) и H A , H B , H C (основания высот треугольника △ ABC и вершины ортоцентрического треугольника).
Ортоцентрическая система и ее ортоцентрические оси
Ортоцентрическая ось, связанная с нормализованной ортоцентрической системой A, B, C, H , где △ ABC — референтный треугольник, представляет собой линию, проходящую через три точки пересечения, образованные при встрече каждой стороны ортоцентрического треугольника с каждой стороной референтного треугольника. Теперь рассмотрим три других возможных треугольника, △ ABH , △ ACH , △ BCH . Каждый из них имеет свою собственную ортоцентрическую ось.
Линии Эйлера и гомотетические ортоцентрические системы

Пусть векторы a , b , c , h определяют положение каждой из четырех ортоцентрических точек, а n = ( a + b + c + h ) / 4 — радиус-вектор N , общего девятиточечного центра. Соединим каждую из четырех ортоцентрических точек с их общим девятиточечным центром и продолжим их в четыре линии. Эти четыре линии теперь представляют собой линии Эйлера четырех возможных треугольников, где продолженная линия HN является линией Эйлера треугольника △ ABC , а продолженная линия AN является линией Эйлера треугольника △ BCH и т. д. Если точка P выбрана на линии Эйлера HN исходного треугольника △ ABC с вектором положения p таким образом, что p = n + α( h – n ) , где α – чистая константа, не зависящая от положения четырех ортоцентрических точек, и еще три точки P A , P B , P C такие, что p a = n + α( a – n ) и т. д., то P, P A , P B , P C образуют ортоцентрическую систему. Эта сгенерированная ортоцентрическая система всегда гомотетична исходной системе из четырех точек с общим девятиточечным центром в качестве гомотетического центра и α – отношением подобия.
Если P выбран в качестве центроида G , то α = –⅓ . Если P выбран в качестве описанного центра O , то α = –1 , и сгенерированная ортоцентрическая система конгруэнтна исходной системе, а также является ее отражением относительно центра девяти точек. В этой конфигурации P A , P B , P C образуют треугольник Джонсона исходного опорного треугольника △ ABC . Следовательно, описанные окружности четырех треугольников △ ABC , △ ABH , △ ACH , △ BCH все равны и образуют набор окружностей Джонсона, как показано на диаграмме рядом.
Дополнительные свойства
Четыре линии Эйлера ортоцентрической системы ортогональны четырем ортоцентрическим осям ортоцентрической системы.
Шесть соединителей, которые соединяют любую пару исходных четырех ортоцентрических точек, создадут пары соединителей, которые ортогональны друг другу, так что они удовлетворяют уравнениям расстояния
где R — общий радиус описанной окружности четырех возможных треугольников. Эти уравнения вместе с законом синусов приводят к тождеству
Теорема Фейербаха утверждает, что окружность девяти точек касается вписанной окружности и трех вневписанных окружностей исходного треугольника. Поскольку окружность девяти точек является общей для всех четырех возможных треугольников в ортоцентрической системе, она касается 16 окружностей, включающих вписанные и вневписанные окружности четырех возможных треугольников.
Любая коника, проходящая через четыре ортоцентрические точки, может быть только прямоугольной гиперболой . Это результат теоремы Фейербаха о кониках, которая гласит, что для всех описанных коник исходного треугольника, которые также проходят через его ортоцентр, геометрическое место центров таких описанных коник образует окружность девяти точек, и что описанные коники могут быть только прямоугольными гиперболами. Геометрическое место точек перспективы этого семейства прямоугольных гипербол всегда будет лежать на четырех ортоцентрических осях. Таким образом, если прямоугольная гипербола проведена через четыре ортоцентрические точки, она будет иметь один фиксированный центр на общей окружности девяти точек, но у нее будет четыре точки перспективы, по одной на каждой из ортоцентрических осей четырех возможных треугольников. Одна точка на окружности девяти точек, которая является центром этой прямоугольной гиперболы, будет иметь четыре различных определения в зависимости от того, какой из четырех возможных треугольников используется в качестве исходного треугольника.
Хорошо известные прямоугольные гиперболы, проходящие через четыре ортоцентрические точки, — это описанные гиперболы Фейербаха, Ержабека и Киперта относительно референциального треугольника △ ABC в нормализованной системе с H в качестве ортоцентра.
Четыре возможных треугольника имеют набор из четырех инкоников, известных как ортоцентрические инконики, которые имеют определенные свойства. Контакты этих инкоников с четырьмя возможными треугольниками происходят в вершинах их общего ортоцентрического треугольника. В нормализованной ортоцентрической системе ортоцентрический инконик, который касается сторон треугольника △ ABC, является вписанным элллипсом, а ортоцентрические инконики трех других возможных треугольников являются гиперболами. Эти четыре ортоцентрических инконика также имеют одну и ту же точку Брианшона H , ортоцентрическую точку, ближайшую к общему девятиточечному центру. Центры этих ортоцентрических инкоников являются симедианными точками K четырех возможных треугольников.
Существует много документированных кубиков, которые проходят через референтный треугольник и его ортоцентр. Циркулярный куб, известный как ортокубический - K006, интересен тем, что он проходит через три ортоцентрические системы, а также через три вершины ортотреугольника (но не ортоцентр ортотреугольника). Три ортоцентрические системы - это инцентр и вневписанный центр, референтный треугольник и его ортоцентр и, наконец, ортоцентр референтного треугольника вместе с тремя другими точками пересечения, которые этот кубик имеет с описанной окружностью референтного треугольника.
Любые две полярные окружности двух треугольников в ортоцентрической системе являются ортогональными . [4]
Примечания
- ^ Кочик, Ежи; Солецки, Анджей (2009). «Распутывание треугольника» (PDF) . American Mathematical Monthly . 116 (3): 228–237.
- ^ Weisstein, Eric W. «Ортоцентрическая система». Из MathWorld — веб-ресурса Wolfram. [1]
- ↑ Джонсон 1929, стр. 182.
- ↑ Джонсон 1929, стр. 177.
Ссылки
- Джонсон, Роджер А. (1929). Современная геометрия: элементарный трактат о геометрии треугольника и окружности. Houghton Mifflin.Переиздано как Advanced Euclidean Geometry . Dover. 1960; 2007. См. особенно главу IX. Три важных момента.
Внешние ссылки
- Эрик В. Вайсштейн . «Ортоцентр», «Теорема Фейербаха», «Коническая теорема Фейербаха», «Гипербола Фейербаха», «Гипербола Йерабека», «Гипербола Киперта», «Ортоинконическая ось», «Ортоосевая ось», «Перспектор». MathWorld .
- Бернар Жиберт Циркумкубический K006
- Кларк Кимберлинг, «Энциклопедия центров треугольников». (Перечисляет около 5000 интересных точек, связанных с любым треугольником.)


