Подвижный клеточный автомат

Эта статья включает список ссылок , связанных чтений или внешних ссылок , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Май 2014 ) ( Узнайте, как и когда удалять это сообщение )

Метод подвижного клеточного автомата

Анимация подвижного клеточного автомата, используемого для моделирования трения на границе двух поверхностей
Тип метода
Непрерывный/Дискретный	Дискретный
Аналитический/Вычислительный	Вычислительный
Характеристики
Под влиянием	клеточный автомат , дискретный элемент
Метод в	вычислительная механика твёрдого тела

Метод подвижного клеточного автомата (MCA) — это метод в вычислительной механике твердого тела, основанный на дискретной концепции. Он обеспечивает преимущества как классического клеточного автомата, так и метода дискретных элементов . Одним из важных преимуществ ^[1] метода MCA является то, что он позволяет проводить прямое моделирование разрушения материала, включая образование повреждений, распространение трещин, фрагментацию и смешивание масс. Трудно моделировать эти процессы с помощью методов механики сплошной среды (например, метода конечных элементов , метода конечных разностей и т. д.), поэтому требуются некоторые новые концепции, такие как перидинамика . Метод дискретных элементов очень эффективен для моделирования зернистых материалов, но взаимные силы между подвижными клеточными автоматами обеспечивают моделирование поведения твердых тел. По мере того, как размер ячейки автомата приближается к нулю, поведение MCA приближается к классическим методам механики сплошной среды . ^[2] Метод MCA был разработан в группе С. Г. Псахье ^[3]

В рамках подхода MCA моделируемый объект рассматривается как набор взаимодействующих элементов/автоматов. Динамика набора автоматов определяется их взаимными силами и правилами их взаимоотношений. Эта система существует и функционирует во времени и пространстве. Ее эволюция во времени и пространстве управляется уравнениями движения. Взаимные силы и правила взаимоотношений между элементами определяются функцией реакции автомата. Эта функция должна быть указана для каждого автомата. В связи с подвижностью автоматов необходимо включить в рассмотрение следующие новые параметры клеточных автоматов: R ⁱ – радиус-вектор автомата; V ⁱ – скорость автомата; ω ⁱ – скорость вращения автомата; θ ⁱ – вектор вращения автомата; m ⁱ – масса автомата; J ⁱ – момент инерции автомата.

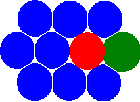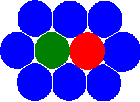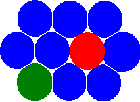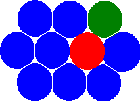
Новая концепция метода MCA основана на введении состояния пары автоматов (отношения взаимодействующих пар автоматов) в дополнение к общепринятому – состоянию отдельного автомата. Отметим, что введение этого определения позволяет перейти от статической сетевой концепции к концепции соседей . В результате этого автоматы получают возможность менять своих соседей, переключая состояния (отношения) пар.

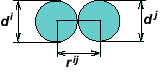
Введение нового типа состояний приводит к новому параметру, который можно использовать в качестве критерия для переключения отношений . Он определяется как автоматное перекрытие параметров  h ^ij . Таким образом, отношение клеточных автоматов характеризуется величиной их перекрытия .

Первоначальная структура формируется путем установления определенных отношений между каждой парой соседних элементов.

В отличие от классического метода клеточных автоматов в методе МКА может переключаться не только один автомат, но и связь пары автоматов . Согласно концепции бистабильных автоматов существуют два типа состояний (связей) пар:

Таким образом, изменение состояния парных отношений контролируется относительными движениями автоматов, а среды, образованные такими парами, можно рассматривать как бистабильные среды.

Эволюция среды MCA описывается следующими уравнениями движения для трансляции :

${\displaystyle {d^{2}h^{ij} \over dt^{2}}=\left({1 \over m^{i}}+{1 \over m^{j}}\right) p^{ij}+\sum _{k\neq j}C(ij,ik)\psi (\alpha _{ij,ik}){1 \over m^{i}}p^{ik}+\ сумма _{l\neq i}C(ij,jl)\psi (\alpha _{ij,jl}){1 \over m^{j}}p^{jl}}$

Здесь - масса автомата , - центральная сила, действующая между автоматами и , - некоторый коэффициент, связанный с передачей параметра h от пары ij к паре ik , - угол между направлениями ij и ik .${\displaystyle м^{я}}$${\displaystyle я}$${\displaystyle p^{ij}}$${\displaystyle я}$${\displaystyle j}$${\displaystyle C(ij,ik)}$${\displaystyle \psi (\alpha _{ij,ik})}$

Из-за конечных размеров подвижных автоматов необходимо учитывать эффекты вращения. Уравнения движения для вращения можно записать следующим образом:

${\displaystyle {d^{2}\theta ^{ij} \over dt^{2}}=\left({q^{ij} \over J^{i}}+{q^{ji} \over J^{j}}\right)\tau ^{ij}+\sum _{k\neq j}S(ij,ik){q^{ik} \over J^{i}}\tau ^{ik}+\sum _{l\neq j}S(ij,jl){q^{jl} \over J^{j}}\tau ^{jl}}$

Здесь Θ ^ij — угол относительного поворота (это параметр переключения, как h ^ij для трансляции), q ^ij — расстояние от центра автомата i до точки контакта автомата j (плечо момента), τ ^ij — тангенциальное взаимодействие пары, — некоторый коэффициент, связанный с передачей параметра Θ из одной пары в другую (он аналогичен уравнению для трансляции).${\displaystyle S(ij,ik)}$${\displaystyle C(ij,ik)}$

Эти уравнения полностью аналогичны уравнениям движения для многочастичного подхода.

Трансляция пары автоматов Безразмерный параметр деформации для трансляции пары автоматов ij можно представить в виде:

${\displaystyle \varepsilon ^{ij}={h^{ij} \over r_{0}^{ij}}={\left(q^{ij}+q^{ji}\right)-\left(d^{i}+d^{j}\right){\big /}2 \over \left(d^{i}+d^{j}\right){\big /}2}}$

В этом случае:

${\displaystyle \left(\Delta {\varepsilon ^{i(j)}}+\Delta {\varepsilon ^{j(i)}}\right){\left(d^{i}+d^{j}\right) \over 2}=V_{n}^{ij}\Delta {t}}$

где Δt – шаг по времени, V _n ^ij – относительная скорость.

Вращение парных автоматов можно рассчитать по аналогии с последними соотношениями трансляции.

Параметр ε ^ij используется как мера деформации автомата i при его взаимодействии с автоматом j . Где q ^ij – расстояние от центра автомата i до точки его контакта с автоматом j ; R ⁱ = d ⁱ /2 ( d ⁱ – размер автомата i ).

В качестве примера рассмотрен образец титана при циклическом нагружении (растяжение – сжатие). Диаграмма нагружения представлена ​​на следующем рисунке:

Схема погрузки	Диаграмма загрузки
	( Красные отметки — экспериментальные данные)

Благодаря мобильности каждого автомата метод MCA позволяет напрямую учитывать такие действия, как:

• смешивание масс
• эффекты проникновения
• химические реакции
• интенсивная деформация
• фазовые превращения
• накопление убытков
• фрагментация и перелом
• образование и развитие трещин

Используя граничные условия разных типов (фиксированные, упругие, вязкоупругие и т.д.), можно имитировать различные свойства окружающей среды, содержащей моделируемую систему. Можно моделировать различные режимы механического нагружения (растяжение, сжатие, сдвиговые деформации и т.д.), задавая дополнительные условия на границах.

• Механика сплошной среды  – раздел физики, изучающий поведение материалов, моделируемых как сплошные среды.
• Механика твёрдого тела  – раздел механики, изучающий твёрдые материалы и их поведение.
• Механика разрушения  – изучение распространения трещин в материалах.
• Перидинамика
• Компьютерное моделирование  – процесс математического моделирования, выполняемый на компьютере.
• Метод дискретных элементов  – Численные методы расчета движения и воздействия большого количества мелких частиц.
• Клеточный автомат  – Дискретная модель, изучаемая в информатике.
• Метод конечных элементов  – численный метод решения физических или инженерных задач.
• Метод конечных разностей  – Класс численных методов

• Псахье, С.Г.; Хорие, Ю.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Алексеев, СВ (ноябрь 1995). «Метод подвижных клеточных автоматов как инструмент моделирования в рамках мезомеханики». Журнал физики . 38 (11): 1157– 1168. Bibcode : 1995RuPhJ..38.1157P. doi : 10.1007/BF00559396. S2CID  120300401.
• Псахье, С.Г.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Моисеенко Д.Д.; Татаринцев Е.М.; Алексеев, СВ. (1998). «Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов». Физическая мезомеханика . 1 (1): 95–108 .( Псахье С.Г.; Коростелев С.Ю.; Смолин А.Ю.; Дмитриев А.И.; Шилько Е.В.; Моисеенко Д.Д.; Татаринцев Е.М.; Алексеев С.В. (1998). "Метод подвижных клеточных автоматов как инструмент физической мезомеханики". Физическая мезомеханика 1 ( 1): 95–108 Проверено 03 марта 2010 г.)
• Псахье, С.Г.; Остермайер, Г.П.; Дмитриев, А.И.; Шилько, Е.В.; Смолин, А.Ю.; Коростелев, С.Ю. (2000). «Метод подвижных клеточных автоматов как новое направление в численной дискретной механике. I. Теоретическое описание». Физическая мезомеханика . 3 (2): 5–13 .( Псахье С.Г.; Остермайер Г.П.; Дмитриев А.И.; Шилько Е.В.; Смолин А.Ю.; Коростелев С.Ю. (2000). «Метод подвижных клеточных Автоматы как новое направление дискретной вычислительной механики I. Теоретическое описание». Физическая мезомеханика . 3 (2): 5– 13 . 03.03.2010 .)
• Psakhie, SG; Horie, Y.; Ostermeyer, GP; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, EV; Dmitryev, AI; Blatnik, S.; Spegel, M.; Zavsek, S. (декабрь 2001 г.). "Метод подвижных клеточных автоматов для моделирования материалов с мезоструктурой" (PDF) . Theoretical and Applied Fracture Mechanics . 37 ( 1– 3): 311– 334. doi :10.1016/S0167-8442(01)00079-9. Архивировано из оригинала (PDF) 2011-07-19.
• Псахье, С.Г.; Смолин, А.Ю.; Стефанов, Ю.П.; Макаров, П.В.; Чертов, МА (2004). «Моделирование поведения сложных сред с использованием совместного использования дискретного и континуального подходов». Письма в журнал технической физики . 30 (9): 712– 714. Bibcode : 2004TePhL..30..712P. doi : 10.1134/1.1804572. S2CID  120067680.
• Симидзу, Y.; Харт, R.; Кундалл, P. (2004). Численное моделирование в микромеханике с помощью методов частиц. CRC Press. ISBN 978-90-5809-679-1. Получено 2010-03-03 .
• Gnecco, E.; Meyer E., ред. (2007). Основы трения и износа в наномасштабе. Springer. ISBN 978-3-540-36806-9. Получено 2010-03-03 .
• Юньлян, Тан; Гуйжун, Тэн; Хайтао, Ли (2008). «Модель MCA для моделирования разрушения микронеоднородных материалов». Журнал наноматериалов . 2008 : 1–7 . doi : 10.1155/2008/946038 . 946038.
• Фомин, В.М.; Андреев, А.Н.; и др. (2008). Механика - от дискретного к непрерывному . Российская академия наук, Сибирское отделение, Институт теоретической и прикладной механики (им. С.А. Христиановича). С. 344. ISBN 978-5-7692-0974-1.( Фомин, В.М.; Андреев А.Н. и др. (2008). Механика - от участкового к сплошному (на русском языке). Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича стр. 344. ISBN. 978-5-7692-0974-1. Архивировано из оригинала 6 октября 2011 . Получено 3 марта 2010 .)
• Смолин, А.Ю.; Роман, Н.В.; Добрынин, СА; Псахье, С.Г. (май–август 2009). «О вращении в методе подвижных клеточных автоматов». Физическая мезомеханика . 12 ( 3–4 ): 124–129 . doi :10.1016/j.physme.2009.07.004.
• Попов, Валентин Львович (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation) . Шпрингер Берлин Гейдельберг. дои : 10.1007/978-3-540-88837-6. ISBN 978-3-540-88836-9.
• Добрынин, С.А. (2010). Разработка метода подвижных ячеистых атомонов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел . Томск: Диссертация на соискание ученой степени кандидата физико-математических наук. С. 130.( Добрынин, С.А. (2010). Развитие методических подвижных клеточных автоматов для создания и распространения упругих волн при контактном разобщении тел (на русском языке). Томск: Диссертация … кандидата физико-математических наук. стр. 130. Дата обращения 3 марта . 2010 .)
• Добрынин, Сергей (2011). Компьютерное моделирование методом подвижного клеточного автомата . Саарбрюккен Германия: LAP LAMBERT Academic Publishing. стр. 132. ISBN 978-3-8443-5954-1.( Добрынин, Сергей (2011). Компьютерное моделирование методом подвижных клеточных автоматов (на русском языке). Саарбрюккен Германия: LAP LAMBERT Academic Publishing. стр. 132. ISBN. 978-3-8443-5954-1. Получено 19 ноября 2011 г.)

• Пакет программного обеспечения MCA
• Программное обеспечение для моделирования материалов в дискретно-континуальном приближении «FEM+MCA»: Номер государственной регистрации в Прикладном научно-исследовательском фонде алгоритмов и программного обеспечения (ПНФАП): 50208802297 / Смолин А.Ю., Зелепугин С.А., Добрынин С.А.; заявитель и центр разработки Томский государственный университет. – дата регистрации 28.11.2008; свидетельство ПНФАП N 11826 от 01.12.2008.