Максимально устойчивая урожайность
В популяционной экологии и экономике максимальный устойчивый улов ( MSY ) теоретически является наибольшим уловом (или добычей), который может быть получен из популяции вида в течение неопределенного периода времени. Основополагающая для понятия устойчивого улова концепция MSY направлена на поддержание размера популяции в точке максимального темпа роста путем вылова особей, которые обычно добавляются к популяции, позволяя популяции продолжать быть продуктивной неопределенно долго. При предположении логистического роста ограничение ресурсов не ограничивает репродуктивные показатели особей, когда популяции невелики, но поскольку особей мало, общий улов невелик. При промежуточных плотностях популяции, также представленных половиной несущей способности , особи способны размножаться с максимальной скоростью. В этой точке, называемой максимальным устойчивым уловом, существует избыток особей, которые могут быть собраны, поскольку рост популяции находится в своей максимальной точке из-за большого количества размножающихся особей. Выше этой точки факторы, зависящие от плотности, все больше ограничивают размножение, пока популяция не достигнет несущей способности. На этом этапе излишков особей для сбора нет, и урожайность падает до нуля. Максимальный устойчивый урожай обычно выше оптимального устойчивого урожая и максимального экономического урожая.
MSY широко используется для управления рыболовством . В отличие от логистической модели ( Шефера ), [1] MSY был уточнен в большинстве современных моделей рыболовства и составляет около 30% от размера неэксплуатируемой популяции. [2] [3] Эта доля различается среди популяций в зависимости от жизненного цикла вида и возрастной селективности метода рыболовства.
История
Концепция MSY как стратегии управления рыболовством была разработана в Белмаре , штат Нью-Джерси , в начале 1930-х годов. [4] [5] [6] Она приобрела популярность в 1950-х годах с появлением моделей избыточного производства с явной оценкой MSY. [1] Как очевидно простая и логичная цель управления, в сочетании с отсутствием других простых целей управления того времени, MSY была принята в качестве основной цели управления несколькими международными организациями (например, IWC , IATTC , [7] ICCAT , ICNAF ) и отдельными странами. [8]
В период с 1949 по 1955 год США маневрировали, чтобы объявить MSY целью международного управления рыболовством (Johnson 2007). Международный договор MSY, который был в конечном итоге принят в 1955 году, давал иностранным флотам право ловить рыбу у любого побережья. Страны, которые хотели исключить иностранные суда, должны были сначала доказать, что их рыба перелавливается. [9]
По мере накопления опыта работы с моделью некоторым исследователям стало очевидно, что ей не хватает возможностей справляться с реальными эксплуатационными сложностями и влиянием трофических и других взаимодействий. В 1977 году Питер Ларкин написал ее эпитафию, оспаривающую цель максимального устойчивого вылова по нескольким причинам: она подвергает популяции слишком большому риску; она не учитывает пространственную изменчивость производительности; она не учитывает виды, не являющиеся объектом рыболовства; она учитывает только выгоды, а не издержки рыболовства; и она чувствительна к политическому давлению. [10] Фактически, ни одно из этих критических замечаний не было направлено на устойчивость как цель. Первый отметил, что поиск абсолютного MSY с неопределенными параметрами был рискованным. Остальные указывают, что цель MSY не была целостной; она не учитывает слишком много важных характеристик. [9]
Некоторые менеджеры начали использовать более консервативные рекомендации по квотам, но влияние модели MSY на управление рыболовством все еще преобладало. Даже когда научное сообщество начало подвергать сомнению целесообразность и эффективность MSY как цели управления, [10] [11] она была включена в Конвенцию ООН по морскому праву 1982 года , тем самым обеспечив ее интеграцию в национальные и международные акты и законы о рыболовстве. [8] По словам Уолтерса и Магуайра, «институциональная машина была приведена в движение», достигнув кульминации в начале 1990-х годов с крахом северной трески . [12]
Моделирование MSY
Рост населения
Ключевое предположение, лежащее в основе всех моделей устойчивого сбора урожая , таких как MSY, заключается в том, что популяции организмов растут и заменяют себя, то есть они являются возобновляемыми ресурсами. Кроме того, предполагается, что поскольку темпы роста, выживаемости и репродуктивности увеличиваются, когда сбор урожая снижает плотность популяции , [4] они производят избыток биомассы, которую можно собирать. В противном случае устойчивый сбор урожая был бы невозможен.
Другое предположение о сборе возобновляемых ресурсов заключается в том, что популяции организмов не продолжают расти бесконечно; они достигают равновесного размера популяции, который возникает, когда количество особей соответствует ресурсам, доступным популяции (т.е. предполагается классический логистический рост ). При этом равновесном размере популяции, называемом пропускной способностью , популяция остается стабильной. [13]
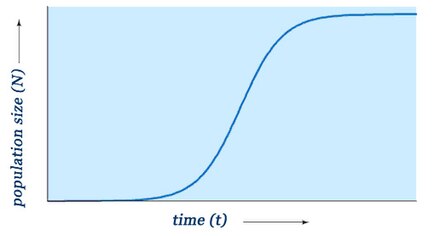
Логистическая модель (или логистическая функция ) — это функция, которая используется для описания ограниченного роста популяции при предыдущих двух предположениях. Логистическая функция ограничена в обоих крайних случаях: когда нет особей для воспроизводства и когда есть равновесное число особей (т. е. при пропускной способности ). В логистической модели скорость роста популяции между этими двумя пределами чаще всего предполагается сигмоидальной (рисунок 1). Существуют научные доказательства того , что некоторые популяции растут логистическим образом в направлении устойчивого равновесия — часто приводимым примером является логистический рост дрожжей .
Уравнение, описывающее логистический рост, имеет вид: [13]
- (уравнение 1.1)
Значения параметров:
- =Численность популяции в момент времени t
- =Пропускная способность популяции
- = Численность популяции в нулевой момент времени
- = внутренняя скорость роста населения (скорость, с которой население растет, когда оно очень мало)
Используя логистическую функцию, можно рассчитать численность популяции в любой точке , если известны , и .

Дифференцируя уравнение 1.1, получаем выражение для того, как скорость роста популяции увеличивается с ростом N. Сначала скорость роста популяции высокая, но по мере роста популяции она начинает замедляться, пока не достигнет максимального значения, после чего начинает снижаться (рисунок 2).
Уравнение для рисунка 2 является дифференциалом уравнения 1.1 ( модель роста Ферхюльста 1838 года ): [13]
- (уравнение 1.2)
можно понимать как изменение численности населения (N) относительно изменения во времени (t). Уравнение 1.2 является обычным способом, с помощью которого логистический рост представляется математически, и имеет несколько важных особенностей. Во-первых, при очень малых размерах популяции значение мало, поэтому темп роста популяции приблизительно равен , то есть популяция растет экспоненциально со скоростью r (внутренняя скорость роста популяции). Несмотря на это, темп роста популяции очень низок (низкие значения на оси Y рисунка 2), потому что, хотя каждая особь размножается с высокой скоростью, размножающихся особей немного. И наоборот, когда популяция большая, значение приближается к 1, эффективно сводя члены в скобках уравнения 1.2 к нулю. Эффект заключается в том, что темп роста популяции снова очень низок, потому что либо каждая особь едва размножается, либо показатели смертности высоки. [13] В результате этих двух крайностей темп роста популяции максимален при промежуточной популяции или половине емкости ( ).
Модель MSY

Самый простой способ моделирования сбора урожая — это модификация логистического уравнения таким образом, чтобы определенное количество особей непрерывно удалялось: [13]
- (уравнение 1.3)
Где H представляет собой количество особей, удаляемых из популяции, то есть скорость сбора урожая. Когда H постоянна, популяция будет находиться в равновесии, когда количество удаляемых особей будет равно скорости роста популяции (рисунок 3). Равновесный размер популяции при определенном режиме сбора урожая можно найти, когда популяция не растет, то есть когда . Это происходит, когда скорость роста популяции такая же, как скорость сбора урожая:
Рисунок 3 показывает, как скорость роста меняется в зависимости от плотности популяции. При низкой плотности (далеко от пропускной способности) популяция мало пополняется (или «прирастает»), просто потому, что мало организмов, которые могут дать потомство. Однако при высокой плотности существует интенсивная конкуренция за ресурсы, и скорость роста снова низкая, потому что высок уровень смертности. Между этими двумя крайностями скорость роста популяции возрастает до максимального значения ( ). Эта максимальная точка представляет собой максимальное количество особей, которые могут быть добавлены к популяции естественными процессами. Если из популяции будет удалено больше особей, популяция рискует исчезнуть. [14] Максимальное количество, которое может быть собрано устойчивым образом, называемое максимальным устойчивым урожаем, определяется этой максимальной точкой.
Рисунок 3 также показывает несколько возможных значений для скорости сбора урожая, H. При , есть две возможные точки равновесия популяции: низкая численность популяции ( ) и высокая ( ). При , немного более высокая скорость сбора урожая, однако есть только одна точка равновесия (при ), которая является размером популяции, который производит максимальную скорость роста. При логистическом росте эта точка, называемая максимальной устойчивой урожайностью, находится там, где размер популяции составляет половину пропускной способности (или ). Максимальная устойчивая урожайность - это самая большая урожайность, которую можно получить от популяции в состоянии равновесия. На рисунке 3, если больше , сбор урожая превысит способность популяции к самовосполнению при любой численности популяции ( на рисунке 3). Поскольку скорость сбора урожая выше скорости роста популяции при всех значениях , эта скорость сбора урожая не является устойчивой.
Важной особенностью модели MSY является то, как собираемые популяции реагируют на колебания окружающей среды или незаконный вылов. Рассмотрим популяцию, собираемую при постоянном уровне вылова . Если популяция падает (из-за плохой зимы или незаконного вылова), это ослабит зависящее от плотности регулирование популяции и увеличит урожайность, вернув популяцию к , устойчивому равновесию. В этом случае отрицательная обратная связь создает стабильность. Однако нижняя точка равновесия для постоянного уровня вылова нестабильна; крах популяции или незаконный вылов снизят урожайность популяции еще ниже текущего уровня вылова, создавая положительную обратную связь, ведущую к вымиранию. Вылов при также потенциально нестабилен. Небольшое уменьшение популяции может привести к положительной обратной связи и вымиранию, если режим вылова ( ) не будет сокращен. Таким образом, некоторые считают вылов при MSY небезопасным по экологическим и экономическим причинам. [14] [15] Сама модель MSY может быть изменена для вылова определенного процента популяции или с постоянными ограничениями усилий, а не фактического числа, тем самым избегая некоторых ее нестабильностей. [14]
Точка равновесия MSY полустабильна – небольшое увеличение размера популяции компенсируется, небольшое уменьшение приводит к вымиранию, если H не уменьшается. Поэтому добыча при MSY опасна, поскольку находится на острие ножа – любое небольшое снижение популяции приводит к положительной обратной связи, при этом популяция быстро сокращается до вымирания, если количество вылавливаемых особей остается прежним. [14] [15]
Формула для максимального устойчивого урожая ( ) представляет собой одну четвертую максимальной популяции или пропускной способности ( ), умноженную на внутреннюю скорость роста ( ). [16]
Для демографически структурированного населения
Принцип MSY часто справедлив и для популяций со структурой по возрасту. [17] Расчеты могут быть более сложными, а результаты часто зависят от того, возникает ли зависимость от плотности на личиночной стадии (часто моделируемой как зависящее от плотности размножение) и/или на других стадиях жизни. [18] Было показано, что если зависимость от плотности действует только на личинку, то существует оптимальная стадия жизни (размер или возрастной класс) для сбора урожая, без сбора урожая на всех других стадиях жизни. [17] Следовательно, оптимальная стратегия состоит в том, чтобы собирать эту наиболее ценную стадию жизни на MSY. [19] Однако в моделях со структурой по возрасту и стадиям постоянный MSY не всегда существует. В таких случаях циклический сбор урожая является оптимальным, когда урожай и ресурсы колеблются по размеру с течением времени. [20] Кроме того, стохастичность окружающей среды взаимодействует с демографически структурированными популяциями принципиально иными способами, чем для неструктурированных популяций при определении оптимального сбора урожая. Фактически, оптимальная биомасса, которую следует оставить в океане при вылове в условиях MSY, может быть как выше, так и ниже, чем в аналогичных детерминированных моделях, в зависимости от деталей функции пополнения, зависящей от плотности, если в модель также включена структура стадий. [21]
Выводы из модели MSY
Начало сбора ранее не собранной популяции всегда приведет к уменьшению ее размера. То есть, собранная популяция не сможет оставаться на уровне своей первоначальной емкости. Вместо этого популяция либо стабилизируется на новом, более низком равновесном размере, либо, если скорость сбора слишком высока, сократится до нуля.
Причина, по которой популяции могут устойчиво собираться, заключается в том, что они демонстрируют реакцию, зависящую от плотности. [14] [15] Это означает, что при любом размере популяции ниже K популяция производит избыточный урожай, который доступен для сбора без уменьшения размера популяции. Зависимость от плотности является регуляторным процессом, который позволяет популяции вернуться к равновесию после возмущения. Логистическое уравнение предполагает, что зависимость от плотности принимает форму отрицательной обратной связи. [15]
Если постоянное число особей изымается из популяции на уровне, превышающем MSY, популяция сократится до вымирания. Изъятие ниже уровня MSY приводит к стабильной равновесной популяции, если начальная популяция превышает нестабильный равновесный размер популяции.
Использование MSY
MSY особенно повлиял на управление возобновляемыми биологическими ресурсами, такими как коммерчески важные рыбы и дикие животные. В терминах рыболовства максимальный устойчивый вылов (MSY) — это самый большой средний улов, который может быть получен из запаса в существующих условиях окружающей среды. [22] MSY нацелен на баланс между слишком большим и слишком малым выловом, чтобы поддерживать популяцию на некотором промежуточном уровне изобилия с максимальной скоростью воспроизводства.
Что касается MSY, максимальный экономический вылов (MEY) — это уровень улова, который обеспечивает максимальную чистую экономическую выгоду или прибыль обществу. [23] [24] Как и оптимальный устойчивый вылов , MEY обычно меньше MSY.
Ограничения подхода MSY
Хотя это широко практикуется государственными и федеральными правительственными агентствами, регулирующими дикую природу, леса и рыболовство, MSY подверглась резкой критике со стороны экологов и других лиц как по теоретическим, так и по практическим причинам. [15] Концепция максимального устойчивого вылова не всегда легко применима на практике. Проблемы с оценкой возникают из-за плохих предположений в некоторых моделях и отсутствия надежности данных. [8] [25] Биологи, например, не всегда имеют достаточно данных, чтобы четко определить размер популяции и темпы ее роста. Расчет точки, в которой популяция начинает замедляться из-за конкуренции, также очень сложен. Концепция MSY также имеет тенденцию рассматривать всех особей в популяции как идентичных, тем самым игнорируя все аспекты структуры популяции, такие как размер или возрастные классы и их различные темпы роста, выживания и воспроизводства. [25]
В качестве цели управления статическая интерпретация MSY (т. е. MSY как фиксированный улов, который можно ловить из года в год) обычно не подходит, поскольку она игнорирует тот факт, что популяции рыб подвергаются естественным колебаниям (т. е. MSY рассматривает окружающую среду как неизменную) в изобилии и, как правило, в конечном итоге сильно истощаются при стратегии постоянного вылова. [25] Таким образом, большинство ученых-рыболовов теперь интерпретируют MSY в более динамическом смысле как максимальный средний улов (MAY), полученный путем применения определенной стратегии вылова к колеблющемуся ресурсу. [8] Или как оптимальную «стратегию улова», где улов означает количество рыбы, которое должно остаться в океане [а не количество рыбы, которое можно выловить]. Стратегия улова часто является оптимальной стратегией для максимизации ожидаемого улова вылавливаемой, стохастически колеблющейся популяции. [26]
Однако ограничения MSY не означают, что он работает хуже, чем люди, использующие свои наилучшие интуитивные суждения. Эксперименты с участием студентов на занятиях по управлению природными ресурсами показывают, что люди, использующие свой прошлый опыт, интуицию и наилучшие суждения для управления рыболовством, генерируют гораздо меньший долгосрочный урожай по сравнению с компьютером, использующим расчет MSY, даже если этот расчет исходит из неверных моделей динамики популяции. [27]
Более современное описание MSY и его расчет см. в [28].
Оранжевый ерш
Примером ошибок в оценке динамики популяции вида является промысел новозеландского большеротого атланта . Ранние квоты основывались на предположении, что у большеротого атланта довольно короткая продолжительность жизни и он размножается относительно быстро. Однако позже было обнаружено, что большеротый атланта живет долго и размножается медленно (~30 лет). К этому моменту запасы были в значительной степени истощены. [ необходима цитата ]
Критика
Этот подход широко критиковался за игнорирование нескольких ключевых факторов, связанных с управлением рыболовством, и привел к разрушительному краху многих рыболовных хозяйств. Среди биологов, занимающихся охраной природы, он широко рассматривается как опасный и неправильно используемый. [29] [12]
Перелов рыбы
Во всем мире наблюдается кризис мирового рыболовства. [30] В последние годы наблюдается ускоренное снижение производительности многих важных промыслов. [31] Рыболовные промыслы, которые были опустошены в последнее время, включают (но не ограничиваются) промыслом больших китов, промыслом Гранд-Бэнк в западной части Атлантического океана и промыслом перуанских анчоусов. [32] Недавние оценки Продовольственной и сельскохозяйственной организацией Объединенных Наций (ФАО) состояния мирового рыболовства указывают на стабилизацию выгрузки в 1990-х годах, составив около 100 миллионов тонн. [33]
Кроме того, изменился состав мировых уловов. [34] Поскольку рыбаки истощают запасы более крупных и долгоживущих хищных видов рыб, таких как треска, тунец, акула и люциан, они переходят на следующий уровень — к видам, которые, как правило, меньше, живут меньше и менее ценны. [35]
Чрезмерный вылов рыбы — классический пример трагедии общин . [32]
Оптимальная устойчивая урожайность
В популяционной экологии и экономике оптимальная устойчивая урожайность — это уровень усилий (LOE), который максимизирует разницу между общим доходом и общими затратами. Или, когда предельный доход равен предельным затратам. Этот уровень усилий максимизирует экономическую прибыль или ренту от используемого ресурса. Обычно он соответствует уровню усилий ниже, чем максимальный устойчивый урожай. В науке об окружающей среде оптимальная устойчивая урожайность — это наибольший экономический урожай возобновляемого ресурса, достижимый в течение длительного периода времени без снижения способности популяции или ее среды поддерживать продолжение этого уровня урожая.
Смотрите также
- Вся рыба в море: максимальный устойчивый вылов и провал управления рыболовством
- Экологический урожай
- Управление рыболовством
- Список выловленных водных животных по весу
- Максимальная экономическая доходность (MEY)
- Динамика численности населения
- Динамика численности рыбных хозяйств
Ссылки
- ^ ab Schaefer, Milner B. (1954), "Some aspects of the dynamics of populations important to the management of commercial marine fishingeries", Bulletin of the Inter-American Tropical Tuna Commission , 1 (2) (перепечатано в Bulletin of Mathematical Biology, Vol. 53, No. 1/2, pp. 253–279, 1991 ed.): 27–56, doi : 10.1007/BF02464432, hdl : 1834/21257 , S2CID 189885665, архивировано из оригинала 2012-12-12 , извлечено 2017-02-24
- ^ Буске, Н.; Дюшен, Т.; Ривест, Л.-П. (2008). «Переопределение максимального устойчивого урожая для модели популяции Шефера, включая мультипликативный шум окружающей среды» (PDF) . Журнал теоретической биологии . 254 (1): 65–75. Bibcode :2008JThBi.254...65B. doi :10.1016/j.jtbi.2008.04.025. PMID 18571675.[ постоянная мертвая ссылка ]
- ^ Торп, Р. Б.; ЛеКен, У. Дж. Ф.; Люксфорд, Ф.; Колли, Дж. С.; Дженнингс, С. (2015). «Оценка и управление последствиями неопределенности в многовидовой размерно-структурированной модели реагирования популяции и сообщества на рыболовство». Методы в экологии и эволюции . 6 (1): 49–58. Bibcode : 2015MEcEv...6...49T. doi : 10.1111/2041-210X.12292. PMC 4390044. PMID 25866615.
- ^ ab Russell, ES (1931). «Некоторые теоретические соображения по проблеме «перелова»». Журнал морской науки ICES . 6 (1): 3–20. doi :10.1093/icesjms/6.1.3. ISSN 1054-3139.
- ^ Хьорт, Дж.; Ян, Г.; Оттестад, П. (1933). «Оптимальный улов». Хвалрадец Скрифтер . 7 : 92–127.
- ^ Грэм, М. (1935). «Современная теория эксплуатации рыболовства и ее применение к тралению в Северном море». Журнал морской науки ICES . 10 (3): 264–274. doi :10.1093/icesjms/10.3.264. ISSN 1054-3139.
- ^ IATTC, Межамериканская комиссия по тропическому тунцу
- ^ abcd Mace, PM (2001). «Новая роль MSY в одновидовых и экосистемных подходах к оценке и управлению запасами рыбных хозяйств» (PDF) . Рыба и рыболовство . 2 (1): 2–32. Bibcode :2001AqFF....2....2M. doi :10.1046/j.1467-2979.2001.00033.x.
- ^ ab Botsford, LW; Castilla, JC; Peterson, CH (1997). «Управление рыболовством и морскими экосистемами». Science . 277 (5325): 509–515. doi :10.1126/science.277.5325.509.
- ^ ab Larkin, PA (1977). «Эпитафия концепции максимального устойчивого вылова». Труды Американского рыболовного общества . 106 (1): 1–11. Bibcode : 1977TrAFS.106....1L. doi : 10.1577/1548-8659(1977)106<1:AEFTCO>2.0.CO;2. ISSN 0002-8487.
- ^ Sissenwine, MP (1978). «Является ли MSY адекватной основой для оптимального вылова?». Рыболовство . 3 (6): 22–42. Bibcode :1978Fish....3f..22S. doi :10.1577/1548-8446(1978)003<0022:IMAAFF>2.0.CO;2.
- ^ ab Walters, C ; Maguire, J (1996). «Уроки оценки запасов из-за коллапса северной трески». Обзоры по биологии рыб и рыболовству . 6 (2): 125–137. Bibcode :1996RFBF....6..125W. doi :10.1007/bf00182340. S2CID 20224324.
- ^ abcde Милнер-Галланд и Мейс 1998, стр. 14-17.
- ^ abcde Дженнингс, С., Кайзер, М.Дж. и Рейнольдс, Дж.Д. (2001), Экология морского рыболовства Blackwell Science Ltd. Молден, Массачусетс. ISBN 0-632-05098-5
- ^ abcde Милнер-Гулланд, Э. Дж., Мейс, Р. (1998), Сохранение биологических ресурсов Wiley-Blackwell. ISBN 978-0-86542-738-9 .
- ^ Болден, Э.Г., Робинсон, У.Л. (1999), Экология и управление дикой природой, 4-е изд. Prentice-Hall, Inc., Аппер Сэддл Ривер, Нью-Джерси. ISBN 0-13-840422-4
- ^ ab Рид, Уильям Дж. (1980-01-01). «Оптимальный сбор урожая в нелинейной модели популяции». Биометрия . 36 (4): 579–593. doi :10.2307/2556112. JSTOR 2556112.
- ^ Бусеккин, Рауф; Хритоненко, Натали; Яценко, Юрий (2013). Оптимальное управление возрастной структурой населения в экономике, демографии и окружающей среде. Routledge. ISBN 978-1136920936.
- ^ Getz, Wayne M. (1980-01-01). «Проблема предельного устойчивого урожая в нелинейно-возрастных популяциях». Mathematical Biosciences . 48 (3–4): 279–292. doi :10.1016/0025-5564(80)90062-0. ISSN 0025-5564. Архивировано из оригинала 2017-02-03 . Получено 2017-01-28 .
- ^ Тахвонен, Олли (2009). «Оптимальный вылов популяций рыб с возрастной структурой». Экономика морских ресурсов . 24 (2): 147–169. doi :10.5950/0738-1360-24.2.147. S2CID 153448834.
- ^ Холден, Мэтью Х.; Конрад, Джон М. (2015-11-01). «Оптимальный уход в структурированном рыболовстве со стохастичностью окружающей среды». Математические биологические науки . 269 : 76–85. doi : 10.1016/j.mbs.2015.08.021. PMID 26362229.
- ^ Национальный исследовательский совет (NRC). 1998. Улучшение оценки рыбных запасов. National Academy Press, Вашингтон, округ Колумбия.
- ^ Кларк, CW (1990), Математическая биоэкономика: оптимальное управление возобновляемыми ресурсами , 2-е изд. Wiley-Interscience, Нью-Йорк
- ^ Национальная служба морского рыболовства (NMFS). 1996. Наши живые океаны: отчет о состоянии живых морских ресурсов США 1995. Технический меморандум NOAA NMFS0F/SPO-19. NMFS, Силвер-Спрингс, Мэриленд.
- ^ abc Таунсенд, CR, Бегон, M., и Харпер, JL (2008), Основы экологии Blackwell Publishing. ISBN 978-1-4051-5658-5
- ^ Рид, Уильям Дж. (1979-12-01). «Оптимальные уровни пропуска в стохастических и детерминированных моделях сбора урожая». Журнал экологической экономики и управления . 6 (4): 350–363. Bibcode : 1979JEEM....6..350R. doi : 10.1016/0095-0696(79)90014-7.
- ^ Холден, Мэтью Х.; Эллнер, Стивен П. (2016-07-01). «Человеческое суждение против количественных моделей для управления экологическими ресурсами». Экологические приложения . 26 (5): 1553–1565. arXiv : 1603.04518 . Bibcode : 2016EcoAp..26.1553H. doi : 10.1890/15-1295. ISSN 1939-5582. PMID 27755756. S2CID 1279459.
- ^ Maunder, MN (2008). «Максимальный устойчивый урожай». Энциклопедия экологии . С. 2292–2296. doi :10.1016/B978-008045405-4.00522-X. ISBN 9780080454054.
- ^ Ларкин П.А. (1977) «Эпитафия концепции максимального устойчивого улова» [ постоянная неработающая ссылка ] Труды Американского общества рыболовства , 106 : 1–11.
- ^ sciencemag.org Ворм, Борис и др. «Влияние потери биоразнообразия на экосистемные услуги океана», Science, 3 ноября 2006 г.
- ^ Кристи, Ф.Т. и Скотт, А.Д. (1965), Общее богатство в океаническом рыболовстве , Johns Hopkins Press, Балтимор
- ^ ab Clark, CW (1973). «Экономика чрезмерной эксплуатации». Science . 118 (4100): 630–634. Bibcode :1973Sci...181..630C. doi :10.1126/science.181.4100.630. PMID 17736970. S2CID 30839110.
- ^ ФАО, Обзор состояния мировых морских рыбных ресурсов, Технический документ ФАО 335 (1994).
- ^ Робертс, К. (2007), Неестественная история моря , Island Press. ISBN 978-1-59726-102-9
- ^ Pauly, D. (1998). «Вылов морских пищевых сетей». Science . 279 (5352): 860–863. Bibcode :1998Sci...279..860P. doi :10.1126/science.279.5352.860. ISSN 0036-8075. PMID 9452385.





















