Максима (программное обеспечение)

Максима

Скриншот Maxima, строящего 2D-график функции с помощью пакета gnuplot-x11, работающего на Ubuntu Linux
Разработчик(и)	Группа Macsyma в проекте MAC и добровольцы-участники
Первоначальный выпуск	1982 ; 42 года назад (1982)
Стабильный релиз	5.47.0 [1]  / 1 июня 2023 г. ; 16 месяцев назад (1 June 2023)
Репозиторий	sourceforge.net/p/maxima/code/ci/master/tree/
Написано в	Общий Лисп
Операционная система	Кроссплатформенный
Тип	Математическое программное обеспечение
Лицензия	GPL
Веб-сайт	maxima.sourceforge.io

Maxima ( / ˈ m æ k s ɪ m ə / ) — мощный программный пакет для выполнения вычислений компьютерной алгебры в математике и физических науках. Он написан на Common Lisp и работает на всех платформах POSIX , таких как macOS , Unix , BSD и Linux , а также под Microsoft Windows и Android . Это бесплатное программное обеспечение, выпущенное на условиях GNU General Public License (GPL).

Maxima основана на версии Macsyma 1982 года , которая была разработана в Массачусетском технологическом институте при финансировании Министерства энергетики США и других правительственных агентств. Версия Macsyma поддерживалась Биллом Шелтером с 1982 года до его смерти в 2001 году. В 1998 году Шелтер получил разрешение от Министерства энергетики на выпуск своей версии под лицензией GPL. Эта версия, теперь называемая Maxima, поддерживается независимой группой пользователей и разработчиков. Maxima не включает ни одной из многочисленных модификаций и улучшений, внесенных в коммерческую версию Macsyma в 1982–1999 годах. Хотя основная функциональность остается схожей, код, зависящий от этих улучшений, может не работать в Maxima, а ошибки, которые были исправлены в Macsyma, могут по-прежнему присутствовать в Maxima, и наоборот. Maxima приняла участие в Google Summer of Code в 2019 году в рамках Международного координационного центра по нейроинформатике . ^[2]

Как и большинство систем компьютерной алгебры, Maxima поддерживает множество способов реорганизации символических алгебраических выражений, таких как факторизация полиномов , вычисление наибольшего общего делителя полиномов , расширение, разделение на действительную и мнимую части и преобразование тригонометрических функций в показательные и наоборот. Она имеет множество методов упрощения алгебраических выражений, включающих тригонометрические функции, корни и показательные функции. Она может вычислять символические первообразные («неопределенные интегралы»), определенные интегралы и пределы . Она может выводить замкнутые ряды , а также члены рядов Тейлора-Маклорена - Лорана . Она может выполнять матричные манипуляции с символическими записями.

Maxima — это система общего назначения, и специальные вычисления, такие как факторизация больших чисел , манипулирование чрезвычайно большими многочленами и т. д., иногда лучше выполнять в специализированных системах.

Maxima специализируется на символьных операциях , но также предлагает числовые возможности ^[3], такие как целые числа произвольной точности , рациональные числа и числа с плавающей точкой , ограниченные только ограничениями по пространству и времени.

Maxima включает в себя полный язык программирования с синтаксисом, подобным ALGOL, но семантикой, подобной Lisp . Он написан на Common Lisp и может быть доступен программно и расширен, поскольку базовый Lisp может быть вызван из Maxima. Он использует gnuplot для рисования.

Для вычислений, интенсивно использующих числа с плавающей точкой и массивы, в Maxima имеются трансляторы с языка Maxima на другие языки программирования (в частности, Fortran ), которые могут выполняться более эффективно.

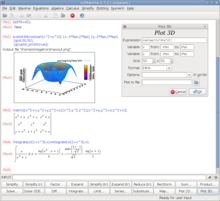
Для Maxima доступны различные графические пользовательские интерфейсы (GUI):

• wxMaxima ^[4] — это высококачественный графический интерфейс, использующий фреймворк wxWidgets . wxMaxima предоставляет ячеистую структуру, похожую на блокнот Mathematica, как показано на рисунке справа.
• Существует ядро ​​для проекта Jupyter , гибкого графического интерфейса в стиле блокнота , написанного на Python . ^[5]
• GMaxima — это интерфейс Maxima, использующий GTK+ . ^[6]
• Cantor , используя Qt , может взаимодействовать с Maxima (вместе с SageMath , R и KAlgebra ) ^[7]
• Программы математических редакторов GNU TeXmacs и LyX могут использоваться для предоставления интерактивного графического интерфейса для Maxima, как и SageMath. Другие варианты включают фронтенд Imaxima, а также режим взаимодействия Emacs и XEmacs , который активируется Imaxima.
• Каяли ^[8]
• Climaxima, ^[9] интерфейс на основе CLIM . ^[10]

bfloat ( sqrt ( 2 )), fpprec = 40 ; 

${\displaystyle 1.41421356237309504880168872420969807857\cdot 10^{0}}$

f ( х ) := х ^ 3 $ж ( 4 );

${\displaystyle 64}$

развернуть (( а - б ) ^ 3 );

${\displaystyle -b^{3}+3ab^{2}-3a^{2}b+a^{3}}$

фактор ( x ^ 2 - 1 );

${\displaystyle (x-1)(x+1)}$

${\displaystyle x^{2}+a\ x+1=0}$

решить ( x ^ 2 + a * x + 1 , x );     

${\displaystyle [x=-{\Biggl (}{\frac {{\sqrt {a^{2}-4}}+a}{2}}{\Biggr )},x={\frac {{\sqrt {a^{2}-4}}-a}{2}}]}$

${\displaystyle \cos x=x}$

найти_корень ( cos ( x ) = x , x , 0 , 1 );     

${\displaystyle 0.7390851332151607}$

bf_find_root ( cos ( x ) = x , x , 0 , 1 ), fpprec = 50 ;        

${\displaystyle 7.3908513321516064165531208767387340401341175890076\cdot 10^{-1}}$

${\displaystyle \int x^{2}+\cos x\ dx}$

интегрировать ( x ^ 2 + cos ( x ), x );   

${\displaystyle \sin x+{\frac {x^{3}}{3}}}$

${\displaystyle \int _{0}^{1}{\frac {1}{x^{3}+1}}\,dx}$

интегрировать ( 1 / ( x ^ 3 + 1 ), x , 0 , 1 ), ratsimp ;      

${\displaystyle {\frac {{\sqrt {3}}\log 2+\pi }{3^{\frac {3}{2}}}}}$

${\displaystyle \int _{0}^{2}\sin(\sin(x))\,dx}$

quad_qags ( sin ( sin ( x )), x , 0 , 2 )[ 1 ];   

${\displaystyle 1.247056058244003}$

${\displaystyle {d^{3} \over dx^{3}}\cos ^{2}x}$

дифф ( cos ( x ) ^ 2 , x , 3 );  

${\displaystyle 8\cos {x}\sin {x}}$

${\displaystyle \lim _{x\to \infty }{\frac {1+\sinh {x}}{e^{x}}}}$

предел (( 1 + sinh ( x )) / exp ( x ), x , inf );  

${\displaystyle {\frac {1}{2}}}$

простые числа ( 10 , 20 ); 

${\displaystyle [11,13,17,19]}$

фиба ( 10 );

${\displaystyle 55}$

${\displaystyle \sum _{x=1}^{\infty }{\frac {1}{x^{2}}}}$

сумма ( 1 / х ^ 2 , х , 1 , инф ), симпсум ;    

${\displaystyle {\frac {\pi ^{2}}{6}}}$

Тейлор ( sin ( x ), x , 0 , 9 );   

${\displaystyle x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{120}}-{\frac {x^{7}}{5040}}+{\frac {x^{9}}{362880}}}$

niceindices ( powerseries ( cos ( x ), x , 0 ));  

${\displaystyle \sum _{i=0}^{\infty }{\frac {(-1)^{i}x^{2i}}{(2i)!}}}$

bessel_j ( 0 , 4.5 ); 

${\displaystyle -0.3205425089851214}$

airy_ai ( 1.5 );

${\displaystyle 0.07174949700810543}$

• Сравнение систем компьютерной алгебры
• SageMath — бесплатное математическое программное обеспечение, которое заимствует множество библиотек из Maxima

• Тимберлейк, Тодд Кин; Миксон-младший, Дж. Уилсон (2015). Классическая механика с Maxima . Springer. ISBN 978-1-4939-3206-1.

В Wikibooks есть книга по теме: Maxima

На Викискладе есть медиафайлы по теме Maxima (программное обеспечение) .

• Официальный сайт
• wxMaxima