Математика судоку

Математику можно использовать для изучения головоломок судоку , чтобы ответить на такие вопросы, как «Сколько существует заполненных сеток судоку?», «Каково минимальное количество подсказок в правильной головоломке?» и «Какими способами сетки судоку могут быть симметричными?», используя комбинаторику и теорию групп .
Анализ судоку обычно делится на анализ свойств нерешённых головоломок (таких как минимально возможное количество данных подсказок) и анализ свойств решённых головоломок. Первоначальный анализ был в основном сосредоточен на перечислении решений, и результаты впервые появились в 2004 году. [1]
Для классического судоку количество заполненных сеток составляет 6 670 903 752 021 072 936 960 (6,671 × 10 21 ), что сводится к 5 472 730 538 существенно различных решений при преобразованиях, сохраняющих действительность. Существует 26 возможных типов симметрии , но они могут быть найдены только в примерно 0,005% всех заполненных сеток. Обычная головоломка с единственным решением должна иметь не менее 17 подсказок. Существует решаемая головоломка с не более чем 21 подсказкой для каждой решенной сетки. Самая большая минимальная головоломка, найденная до сих пор, имеет 40 подсказок в 81 ячейке.
Пазлы
Минимальное количество данных
Обычные судоку ( правильные головоломки) имеют единственное решение. Минимальное судоку — это судоку, из которого нельзя удалить ни одной подсказки, оставляя его правильным судоку. Различные минимальные судоку могут иметь разное количество подсказок. В этом разделе обсуждается минимальное количество данных для правильных головоломок.
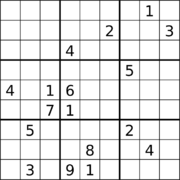
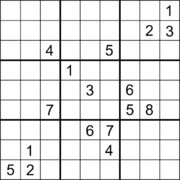
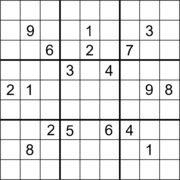
Обычный судоку
 |  |  |
 |  |
Было найдено много судоку с 17 подсказками, хотя их поиск — нетривиальная задача. [2] [3] В статье 2014 года Гари МакГвайра, Бастиана Тугемана и Жиля Сиварио было доказано, что минимальное количество подсказок в любой правильной судоку составляет 17 с помощью исчерпывающего компьютерного поиска, основанного на перечислении множеств попаданий . [4]
Симметричное судоку
Наименьшее количество подсказок в судоку с двусторонней диагональной симметрией (симметрия вращения 180°) считается равным 18, и по крайней мере в одном случае такой судоку также демонстрирует автоморфизм . Известно, что существует судоку с 24 подсказками, диэдральной симметрией (симметрия вращения 90°, которая также включает симметрию относительно обеих ортогональных осей, симметрию вращения 180° и диагональную симметрию), но неизвестно, является ли это количество подсказок минимальным для этого класса судоку. [5]
Общее количество минимальных головоломок
Число минимальных судоку (судоку, в которых ни одна подсказка не может быть удалена без потери уникальности решения) точно не известно. Однако статистические методы в сочетании с генератором ( 'Unbiased Statistics of a CSP – A Controlled-Bias Generator' ), [6] показывают, что существует приблизительно (с относительной ошибкой 0,065%):
- 3,10 × 10 37 различных минимальных головоломок,
- 2,55 × 1025 минимальных головоломок, которые не являются псевдоэквивалентными (т.е. одинаковыми, но все экземпляры одной цифры заменены другой цифрой).
Варианты
Существует множество вариантов судоку, частично характеризующихся размером ( N ) и формой их областей . Если не указано иное, обсуждение в этой статье предполагает классическое судоку, т. е. N =9 (сетка 9×9 и области 3×3). Прямоугольная судоку использует прямоугольные области размерностью строк-столбцов R × C. Другие варианты включают в себя области с неправильной формой или с дополнительными ограничениями (гиперкуб).
Регионы также называются блоками или ящиками . Полоса — это часть сетки, которая инкапсулирует три строки и три ящика, а стек — это часть сетки, которая инкапсулирует три столбца и три ящика. Головоломка — это частично заполненная сетка , а начальные значения — это данные или подсказки . Правильная головоломка имеет единственное решение. Минимальная головоломка — это правильная головоломка, из которой нельзя удалить ни одну подсказку без введения дополнительных решений.
Решение судоку с точки зрения игрока было исследовано в книге Дени Бертье «Скрытая логика судоку» (2007) [7] , в которой рассматриваются такие стратегии, как «скрытые xy-цепочки».
Математический контекст
Известно , что общая задача решения головоломок судоку на сетках n 2 × n 2 из n × n блоков является NP-полной . [8]
Головоломка может быть выражена как задача раскраски графа . [9] Цель состоит в том, чтобы построить 9-раскраску конкретного графа, заданную частичной 9-раскраской. Граф судоку имеет 81 вершину, по одной вершине на каждую ячейку. Вершины помечены упорядоченными парами ( x , y ), где x и y — целые числа от 1 до 9. В этом случае две различные вершины, помеченные ( x , y ) и ( x ′, y ′), соединены ребром тогда и только тогда, когда :
- x = x ′ (тот же столбец) или,
- y = y ′ (та же строка) или,
- ⌈ x /3 ⌉ = ⌈ x ′/3 ⌉ и ⌈ y /3 ⌉ = ⌈ y ′/3 ⌉ (та же ячейка 3×3)
Затем головоломка завершается путем присвоения каждой вершине целого числа от 1 до 9 таким образом, чтобы вершинам, соединенным ребром, не было присвоено одинаковое целое число.
Сетка решения судоку также представляет собой латинский квадрат . [9] Существует значительно меньше сеток судоку, чем латинских квадратов, поскольку судоку накладывает дополнительные региональные ограничения.
Судоку из групповых таблиц
Как и в случае латинских квадратов, таблицы (сложения) или умножения ( таблицы Кэли ) конечных групп могут быть использованы для построения судоку и связанных с ними таблиц чисел. А именно, необходимо учитывать подгруппы и факторгруппы :
Возьмем, к примеру, группу пар, добавляя каждый компонент отдельно по модулю некоторого . Опуская один из компонентов, мы внезапно оказываемся в (и это отображение, очевидно, совместимо с соответствующими добавлениями, т.е. это гомоморфизм групп ). Говорят также, что последняя является фактор-группой первой, потому что некоторые когда-то различные элементы становятся равными в новой группе. Однако это также подгруппа, потому что мы можем просто заполнить недостающий компонент с помощью , чтобы вернуться к .
В этом представлении мы записываем пример, Сетка 1 , для .
Каждая область судоку выглядит одинаково на втором компоненте (а именно как подгруппа ), потому что они добавляются независимо от первого. С другой стороны, первые компоненты равны в каждом блоке, и если мы представим каждый блок как одну ячейку, эти первые компоненты показывают один и тот же шаблон (а именно факторгруппу ). Как указано в статье о латинских квадратах, это латинский квадрат порядка .
Теперь, чтобы получить судоку, давайте переставим строки (или, что эквивалентно, столбцы) таким образом, чтобы каждый блок был перераспределен ровно один раз в каждом блоке – например, упорядочим их . Это, конечно, сохраняет свойство латинского квадрата. Более того, в каждом блоке строки имеют различную первую компоненту по построению, и каждая строка в блоке имеет различные записи через вторую компоненту, потому что вторые компоненты блоков изначально образовывали латинский квадрат порядка (из подгруппы ). Таким образом, мы приходим к судоку (переименуйте пары в числа 1...9, если хотите). С примером и перестановкой строк выше мы приходим к Grid 2 .
|
|
Для того, чтобы этот метод работал, обычно не требуется произведение двух групп одинакового размера. Так называемая короткая точная последовательность конечных групп соответствующего размера уже делает эту работу. Попробуйте, например, группу с фактор- и подгруппой . Кажется очевидным (уже из аргументов перечисления), что не все судоку можно сгенерировать таким образом.
Головоломка судоку
Судоку, области которого не являются (обязательно) квадратными или прямоугольными, известно как Jigsaw Sudoku. В частности, квадрат N × N , где N является простым числом, может быть выложен только нерегулярными N -мино . Для малых значений N было вычислено количество способов замостить квадрат (исключая симметрии) (последовательность A172477 в OEIS ). [10] Для N ≥ 4 некоторые из этих мозаик несовместимы ни с одним латинским квадратом; т. е. все головоломки судоку на такой мозаике не имеют решения. [10]
Решения
Ответ на вопрос «Сколько существует сеток судоку?» зависит от определения того, когда похожие решения считаются различными.
Обычный судоку
Все решения
Для перечисления всех возможных решений два решения считаются различными, если какие-либо из соответствующих им (81) значений ячеек различаются. Симметрийные отношения между похожими решениями игнорируются, например, повороты решения считаются различными. Симметрии играют важную роль в стратегии перечисления, но не в подсчете всех возможных решений.
Первое известное решение для полного перечисления было опубликовано QSCGZ (Гюнтером Стертенбринк) в группе новостей rec.puzzles в 2003 году [11] [12], в результате чего было получено 6 670 903 752 021 072 936 960 (6,67 × 10 21 ) различных решений.
В исследовании 2005 года Фельгенгауэр и Джарвис [13] [12] проанализировали перестановки верхней полосы, используемые в допустимых решениях. После того, как были определены симметрии Band1 и классы эквивалентности для частичных сеточных решений, были построены и подсчитаны завершения нижних двух полос для каждого класса эквивалентности. Суммирование завершений по классам эквивалентности, взвешенных по размеру класса, дает общее количество решений как 6 670 903 752 021 072 936 960, подтверждая значение, полученное QSCGZ. Впоследствии это значение было подтверждено много раз независимо. Позднее был разработан второй метод перечисления, основанный на генерации полос, который является значительно менее вычислительно интенсивным. Этот последующий метод привел к необходимости примерно 1/97 от количества циклов вычислений, как и исходные методы, но был значительно сложнее в настройке.
Принципиально разные решения
Группа симметрии судоку
Точная структура группы симметрии судоку может быть выражена кратко с помощью сплетения (≀ ) . Возможные перестановки строк (или столбцов) образуют группу, изоморфную S 3 ≀ S 3 порядка 3! 4 = 1,296. [4] Вся группа перестановок формируется путем применения операции транспонирования (изоморфной C 2 ) к двум копиям этой группы, одной для перестановок строк и одной для перестановок столбцов. Это S 3 ≀ S 3 ≀ C 2 , группа порядка 1,296 2 × 2 = 3,359,232. Наконец, операции перемаркировки коммутируют с операциями перестановки, поэтому полная группа судоку (VPT) равна ( S 3 ≀ S 3 ≀ C 2 ) × S 9 порядка 1 218 998 108 160.
Неподвижные точки и лемма Бернсайда
Множество эквивалентных сеток, которые могут быть получены с помощью этих операций (исключая перемаркировку), образует орбиту сеток под действием группы перестановок . Число существенно различных решений тогда равно числу орбит, которое может быть вычислено с помощью леммы Бернсайда . Неподвижные точки Бернсайда — это сетки, которые либо не изменяются при операции перестановки, либо отличаются только перемаркировкой. Для упрощения вычислений элементы группы перестановок сортируются по классам сопряженности , все элементы которых имеют одинаковое количество неподвижных точек. Оказывается, только 27 из 275 классов сопряженности группы перестановок имеют неподвижные точки; [14] эти классы сопряженности представляют различные типы симметрии (самоподобие или автоморфизм), которые можно найти в завершенных сетках судоку. Используя эту технику, Эд Рассел и Фрейзер Джарвис первыми вычислили количество существенно различных решений судоку, которое составило 5 472 730 538. [14] [15]
Полнота группы симметрии судоку
За исключением перемаркировки, все операции группы симметрии судоку состоят из перестановок ячеек, которые сохраняют решение , что поднимает вопрос о том, все ли такие перестановки ячеек, сохраняющие решение, находятся в группе симметрии. В 2008 году Авив Адлер и Илан Адлер показали, что все перестановки ячеек, сохраняющие решение, содержатся в группе, даже для общих сеток. [16]
Смотрите также
- Комбинаторный взрыв (с кратким изложением количества сеток судоку в сравнении с латинскими квадратами)
- Танцевальные ссылки
- Глоссарий судоку
- Судокян
- Код судоку
Ссылки
- ^ Лин, Ке Ин (2004), «Число судоку», Журнал занимательной математики , 33 (2): 120–24.
- ^ "プログラミングパズル雑談コーナー" . .ic-net.or.jp. Архивировано из оригинала 12 октября 2016 года . Проверено 20 октября 2013 г.
- ^ "Minimum Sudoku". Csse.uwa.edu.au. Архивировано из оригинала 26 ноября 2006 года . Получено 20 октября 2013 года .
- ^ ab McGuire, G.; Tugemann, B.; Civario, G. (2014). «Судоку с 16 подсказками не существует: решение проблемы минимального количества подсказок в судоку». Experimental Mathematics . 23 (2): 190–217. arXiv : 1201.0749 . doi :10.1080/10586458.2013.870056.
- ^ Таалман, Лора (2007), «Серьёзное отношение к судоку», Math Horizons , 15 (1): 5–9, doi :10.1080/10724117.2007.11974720, JSTOR 25678701, S2CID 126371771. См. в частности Рисунок 7, стр. 7.
- ^ Бертье, Денис (4 декабря 2009 г.). "Непредвзятая статистика CSP – генератор контролируемого смещения" . Получено 4 декабря 2009 г.
- ^ Бертье, Денис (ноябрь 2007 г.). Скрытая логика судоку (Второе, исправленное и расширенное издание). Lulu.com. ISBN 978-1847534729.
- ^ Ято, Такаюки; Сета, Такахиро (2003). «Сложность и полнота поиска другого решения и ее применение к головоломкам». Труды IEICE по основам электроники, связи и компьютерных наук . E86-A (5): 1052–1060.
- ^ Льюис, Р. Руководство по раскраске графов: алгоритмы и приложения . Springer International Publishers, 2015.
- ^ ab de Ruiter, Johan (15 марта 2010 г.). «О головоломках-судоку и связанных с ними темах (бакалаврская работа)» (PDF) . Лейденский институт передовой компьютерной науки (LIACS) .
- ^ QSCGZ (Guenter Stertenbrink) (21 сентября 2003 г.). "комбинаторный вопрос по 9x9 (rec.puzzles)". Google Discussiegroepen . Получено 20 октября 2013 г.
- ^ ab Jarvis, Frazer (2 февраля 2008 г.). "Проблемы перечисления судоку". Домашняя страница Frazer Jarvis . University of Sheffield . Получено 20 октября 2013 г.
- ^ Фельгенгауэр, Бертрам; Джарвис, Фрейзер (20 июня 2005 г.), Перечисление возможных сеток судоку (PDF).
- ^ ab Эд Рассел и Фрейзер Джарвис (7 сентября 2005 г.). «Существует 5472730538 существенно различных сеток Судоку... и группа симметрии Судоку». Домашняя страница Фрейзера Джарвиса . Университет Шеффилда . Получено 20 октября 2013 г.
- ↑ Эд Рассел, Фрейзер Джарвис (25 января 2006 г.). «Математика судоку II» (PDF) .
- ^ Адлер, Авив; Адлер, Илан (2008). «Фундаментальные преобразования сеток судоку» (PDF) . Математический спектр . 41 (1): 2–7.
Дальнейшее чтение
- Розенхаус, Джейсон ; Таалман, Лора (2011). Серьёзное отношение к судоку: математика, лежащая в основе самой популярной в мире головоломки с карандашом . Oxford University Press.
Внешние ссылки
- Алгоритм разностной карты В. Элзера также решает судоку
- Головоломка «Судоку» — упражнение по программированию в ограничениях и Visual Prolog 7 Карстена Келера Холста (в Visual Prolog )
- В книге «Квадраты судоку и хроматические многочлены» Герцберга и Мёрти головоломки судоку рассматриваются как задачи раскраски вершин в теории графов .













