Формула усиления Мейсона

Формула усиления Мейсона (MGF) — это метод нахождения передаточной функции линейного графа потока сигналов (SFG). Формула была выведена Сэмюэлем Джефферсоном Мейсоном ^[1] , в честь которого она и названа. MGF — это альтернативный метод нахождения передаточной функции алгебраическим путем путем маркировки каждого сигнала, записи уравнения того, как этот сигнал зависит от других сигналов, а затем решения нескольких уравнений для выходного сигнала в терминах входного сигнала. MGF предоставляет пошаговый метод получения передаточной функции из SFG. Часто MGF можно определить путем проверки SFG. Метод может легко обрабатывать SFG со многими переменными и циклами, включая циклы с внутренними циклами. MGF часто встречается в контексте систем управления , микроволновых схем и цифровых фильтров, поскольку они часто представлены SFG.

Формула выигрыша выглядит следующим образом:

${\displaystyle G={\frac {y_{\text{out}}}{y_{\text{in}}}}={\frac {\sum _{k=1}^{N}{G_{k}\Delta _{k}}}{\Delta \ }}}$

${\displaystyle \Delta =1-\sum L_{i}+\sum L_{i}L_{j}-\sum L_{i}L_{j}L_{k}+\cdots +(-1)^{m}\sum \cdots +\cdots }$

где:

• Δ = определитель графика.
• y _in = переменная входного узла
• y _out = переменная выходного узла
• G = полное усиление между y _in и y _out
• N = общее количество прямых путей между y _in и y _out
• G _k = коэффициент усиления пути k -го прямого пути между y _in и y _out
• L _i = коэффициент усиления контура каждого замкнутого контура в системе
• L _i L _j = произведение коэффициентов усиления контуров любых двух несоприкасающихся контуров (без общих узлов)
• L _i L _j L _k = произведение коэффициентов усиления контуров любых трех попарно несоприкасающихся контуров
• Δ _k = значение кофактора Δ для k- ^го прямого пути, при этом петли, касающиеся k ^-го прямого пути, удалены.

Источник: ^[2]

• Путь: непрерывный набор ветвей, проложенных в указанном ими направлении.
• Прямой путь: путь от входного узла к выходному узлу, в котором ни один узел не затрагивается более одного раза.
• Петля: путь, который начинается и заканчивается в одном и том же узле, при этом ни один узел не затрагивается более одного раза.
• Прирост пути: произведение приростов всех ветвей на пути.
• Коэффициент усиления контура: произведение коэффициентов усиления всех ветвей контура.

1. Составьте список всех прямых путей и их преимуществ и обозначьте их как G _k .
2. Составьте список всех петель и их приростов и обозначьте их как L _i (для i петель). Составьте список всех пар несоприкасающихся петель и произведений их приростов ( L _i L _j ). Составьте список всех попарно несоприкасающихся петель, взятых по три за раз ( L _i L _j L _k ), затем по четыре за раз и так далее, пока не останется ни одной.
3. Вычислите определитель Δ и сомножители Δ _k .
4. Примените формулу.

Требуется определить передаточную функцию от V _in к V _{2 .}

Есть только один прямой путь:

• V _in к V ₁ к I ₂ к V ₂ с усилением${\displaystyle G_{1}=-y_{21}R_{L}\,}$

Существует три цикла:

• V ₁ к I ₁ к V ₁ с усилением ${\displaystyle L_{1}=-R_{\text{in}}y_{11}\,}$
• V ₂ к I ₂ к V ₂ с усилением ${\displaystyle L_{2}=-R_{L}y_{22}\,}$
• V ₁ к I ₂ к V ₂ к I ₁ к V ₁ с усилением ${\displaystyle L_{3}=y_{21}R_{L}y_{12}R_{\text{in}}\,}$

${\displaystyle \Delta =1-(L_{1}+L_{2}+L_{3})+(L_{1}L_{2})\,}$ примечание: L ₁ и L ₂ не касаются друг друга, тогда как L ₃ касается обеих других петель.

${\displaystyle \Delta _{1}=1\,}$ примечание: прямой путь касается всех циклов, поэтому остается только 1 .

${\displaystyle G={\frac {G_{1}\Delta _{1}}{\Delta }}={\frac {-y_{21}R_{L}}{1+R_{\text{in}}y_{11}+R_{L}y_{22}-y_{21}R_{L}y_{12}R_{\text{in}}+R_{\text{in}}y_{11}R_{L}y_{22}}}\,}$

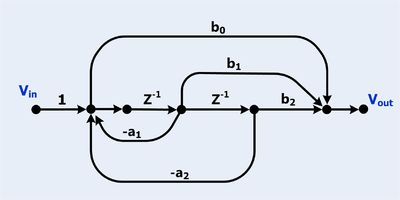
Цифровые фильтры часто изображаются в виде графиков потоков сигналов.

Есть две петли

• ${\displaystyle L_{1}=-a_{1}Z^{-1}\,}$
• ${\displaystyle L_{2}=-a_{2}Z^{-2}\,}$

${\displaystyle \Delta =1-(L_{1}+L_{2})\,}$Обратите внимание, что две петли соприкасаются, поэтому для их произведения термина не существует.

Есть три пути вперед

• ${\displaystyle G_{0}=b_{0}\,}$
• ${\displaystyle G_{1}=b_{1}Z^{-1}\,}$
• ${\displaystyle G_{2}=b_{2}Z^{-2}\,}$

Все прямые пути касаются всех петель, поэтому${\displaystyle \Delta _{0}=\Delta _{1}=\Delta _{2}=1\,}$

${\displaystyle G={\frac {G_{0}\Delta _{0}+G_{1}\Delta _{1}+G_{2}\Delta _{2}}{\Delta }}\,}$

${\displaystyle G={\frac {b_{0}+b_{1}Z^{-1}+b_{2}Z^{-2}}{1+a_{1}Z^{-1}+a_{2}Z^{-2}}}\,}$

Граф потока сигнала имеет шесть петель. Это:

• ${\displaystyle L_{0}=-{\frac {\beta }{sM}}\,}$

• ${\displaystyle L_{1}={\frac {-(R_{M}+R_{S})}{sL_{M}}}\,}$

• ${\displaystyle L_{2}=\,{\frac {-G_{M}K_{M}}{s^{2}L_{M}M}}}$

• ${\displaystyle L_{3}={\frac {-K_{C}R_{S}}{sL_{M}}}\,}$

• ${\displaystyle L_{4}={\frac {-K_{V}K_{C}K_{M}G_{T}}{s^{2}L_{M}M}}\,}$

• ${\displaystyle L_{5}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}$

${\displaystyle \Delta =1-(L_{0}+L_{1}+L_{2}+L_{3}+L_{4}+L_{5})+(L_{0}L_{1}+L_{0}L_{3})\,}$

Есть один прямой путь:

• ${\displaystyle g_{0}={\frac {K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}M}}\,}$

Прямой путь касается всех петель, поэтому кофактор${\displaystyle \Delta _{0}=1}$

И выигрыш от входа к выходу составляет${\displaystyle {\frac {\theta _{L}}{\theta _{C}}}={\frac {g_{0}\Delta _{0}}{\Delta }}\,}$

Правило Мейсона можно сформулировать в простой матричной форме. Предположим, что это переходная матрица графа, где — суммарная пропускаемость ветвей от узла m к узлу n . Тогда усиление от узла m к узлу n графа равно , где${\displaystyle \mathbf {T} }$${\displaystyle t_{nm}=\left[\mathbf {T} \right]_{nm}}$${\displaystyle u_{nm}=\left[\mathbf {U} \right]_{nm}}$

${\displaystyle \mathbf {U} =\left(\mathbf {I} -\mathbf {T} \right)^{-1}}$,

и является единичной матрицей.${\displaystyle \mathbf {I} }$

Правило Мейсона также особенно полезно для вывода функции передачи z-области дискретных сетей, которые имеют внутренние контуры обратной связи, встроенные во внешние контуры обратной связи (вложенные контуры). Если дискретную сеть можно изобразить как граф потока сигнала, то применение правила Мейсона даст функцию передачи H(z) z-области этой сети.

Правило Мейсона может расти факториально, поскольку перечисление путей в ориентированном графе резко возрастает. Чтобы увидеть это, рассмотрим полный ориентированный граф на вершинах, имеющий ребро между каждой парой вершин. Существует форма пути для каждой из перестановок промежуточных вершин. Таким образом, гауссовское исключение более эффективно в общем случае.${\displaystyle n}$${\displaystyle y_{\text{in}}}$${\displaystyle y_{\text{out}}}$${\displaystyle (n-2)!}$

Однако правило Мейсона характеризует передаточные функции взаимосвязанных систем способом, который одновременно является алгебраическим и комбинаторным, что позволяет делать общие утверждения и другие вычисления в теории алгебраических систем. В то время как многочисленные обратные значения возникают во время гауссовского исключения, правило Мейсона естественным образом собирает их в одно квазиобратное значение . Общая форма:

${\displaystyle {\frac {p}{1-q}},}$

Где, как описано выше, представляет собой сумму произведений цикла, каждое из которых обычно попадает в идеал (например, строго каузальные операторы). Дроби этой формы образуют подкольцо поля рациональных функций . Это наблюдение переносится на некоммутативный случай, ^[3] хотя само правило Мейсона тогда должно быть заменено правилом Ригля .${\displaystyle q}$ ${\displaystyle R(1+\langle L_{i}\rangle )^{-1}}$

• График потока сигналов
• Правило Ригля

• Болтон, В. Ньюнес (1998). Карманный справочник по технике управления . Оксфорд: Ньюнес.
• Ван Валкенбург, МЭ (1974). Сетевой анализ (3-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall.