Некоммутативный граф потока сигналов

В теории автоматов и теории управления , разделах математики , теоретической информатики и системной инженерии некоммутативный граф потока сигналов представляет собой инструмент для моделирования ^[1] взаимосвязанных систем и конечных автоматов путем отображения ребер ориентированного графа в кольцо или полукольцо .

Одиночный вес ребра может представлять собой массив импульсных реакций сложной системы (см. рисунок справа) ^[2] или символ алфавита, взятый с входной ленты конечного автомата ^[3] , в то время как граф может представлять собой поток информации или переходы состояний.

Несмотря на то, что эти приложения разнообразны, в их основе лежит во многом одна и та же теория. ^{[4] [5]}

Эта статья может быть запутанной или непонятной для читателей . В частности, что здесь определено, в терминах чего?. Пожалуйста, помогите прояснить статью . Об этом может быть обсуждение на странице обсуждения . ( Сентябрь 2015 г. ) ( Узнайте, как и когда удалить это сообщение )

Рассмотрим n уравнений, содержащих n +1 переменных { x ₀ , x ₁ ,..., x _n }.

${\displaystyle x_{i}=\sum _{j=0}^{n}a_{ij}x_{j},\;\;\;1\leq i\leq n,}$

с элементами _ij в кольце или полукольце R . Свободная переменная x ₀ соответствует исходной вершине v ₀ , таким образом, не имея определяющего уравнения. Каждое уравнение соответствует фрагменту ориентированного графа G =( V , E ) как показано на рисунке.

Веса ребер определяют функцию f от E до R. Наконец, фиксируем выходную вершину v _m . Граф потока сигналов — это набор этих данных S = ( G =( V , E ), v ₀ , v _m V , f  : E → R ). Уравнения могут не иметь решения, но когда они есть,${\displaystyle \в}$

${\displaystyle x_{m}=Tx_{0},}$

с T элемент R, называемый усилением .

Существует несколько ^[2] некоммутативных обобщений правила Мейсона . ^{[ требуется разъяснение ]} Наиболее распространенным является метод обратного цикла (иногда называемый методом прямого обратного цикла (FRL) , имеющим дуальный метод обратного обратного цикла (BRL) ). Первое строгое доказательство ^{[ требуется разъяснение ]} приписывается Риглу, ^[2] поэтому его иногда называют правилом Ригле . ^[6]

Как и в случае с правилом Мейсона , эти ^{[ требуется разъяснение ]} выражения усиления объединяют термины в графо-теоретической манере (петлевые усиления, продукты путей и т. д.). Известно, что они справедливы для произвольного некоммутативного кольца и для полукольца регулярных выражений. ^[5]

Метод ^{[ необходимо разъяснение ]} начинается с перечисления всех путей от входа к выходу, ^{[ необходимо разъяснение ]} индексированных j J. Мы используем следующие определения:${\displaystyle \в}$

• Произведение j -го пути представляет собой (неправильно обозначенный) кортеж из k _j весов ребер вдоль него:

${\ displaystyle p_ {j} = (w_ {k_ {j}} ^ {(j)}, \ ldots, w_ {2} ^ {(j)}, w_ {1} ^ {(j)}).}$^{[ требуется разъяснение ]}

• Разделить вершину v — значит заменить ее источником и стоком с учетом исходной инцидентности и весов (это обратный морфизм графа, переводящий источник и сток в v ).
• Коэффициент усиления петли вершины v относительно подграфа H — это коэффициент усиления от источника к приемнику графа потока сигналов, разделенного в точке v после удаления всех вершин, не входящих в H.
• Каждый путь определяет порядок вершин вдоль него. Вдоль пути j , фактор узла i -го FRL (BRL) равен (1- S _i ^(j) ) ⁻¹ , где S _i ^(j) — это коэффициент усиления петли i -й вершины вдоль j -го относительно подграфа, полученного путем удаления v ₀ и всех вершин перед (позади) ней.

Вклад j -го пути в выигрыш представляет собой произведение вдоль пути, чередующееся между весами произведения пути и факторами узлов:

${\displaystyle T_{j}=\prod _{i=k_{j}}^{1}(1-S_{i}^{(j)})^{-1}w_{i}^{(j)},}$

так что общий выигрыш составляет

${\displaystyle T=\sum _{j\in J}T_{j}.}$

Рассмотрим показанный график потока сигнала . От x до z есть два продукта пути: ( d ) и ( e,a ). Вдоль ( d ) вклады FRL и BRL совпадают, поскольку оба имеют одинаковое усиление контура (разделение которого снова появляется в правом верхнем углу таблицы ниже):

${\displaystyle f+e(1-b)^{-1}c,}$

Умножая его фактор узла и вес пути, его вклад в усиление равен

${\displaystyle T_{d}=\left[1-fe(1-b)^{-1}c\right]^{-1}d.}$

Вдоль пути ( e,a ) FRL и BRL немного отличаются, каждый из них имеет различные разделения вершин y и z, как показано в следующей таблице.

Добавляя к T _d знакопеременное произведение узловых факторов и весов путей, получаем два выражения усиления:

${\displaystyle T^{(FRL)}=\left[1-fe(1-b)^{-1}c\right]^{-1}d+\left[1-fe(1-b)^{-1}c\right]^{-1}e(1-b)^{-1}a,}$

и

${\displaystyle T^{(BRL)}=\left[1-f-e(1-b)^{-1}c\right]^{-1}d+(1-f)^{-1}e\left[1-b-c(1-f)^{e}\right]^{-1}a,}$

Легко видеть, что эти значения одинаковы, используя тождества ( ab ) ⁻¹ = b ⁻¹ a ⁻¹ и a (1- ba ) ⁻¹ =(1- ab ) ⁻¹ a .

Рассмотрим уравнения

${\displaystyle y_{i}=\sum _{j=1}^{2}a_{ij}x_{j}+\sum _{j=1}^{2}b_{ij}y_{j}}$

и

${\displaystyle z_{i}=\sum _{j=1}^{2}c_{ij}y_{j},}$

Эту систему можно смоделировать как скалярный граф потока сигналов с несколькими входами и выходами. Но переменные естественным образом попадают в слои, которые можно собрать в векторы x =( x ₁ , x ₂ ) ^t y =( y ₁ , y ₂ ) ^t и z =( z ₁ , z ₂ ) ^t . Это приводит к гораздо более простому матричному графу потока сигналов , как показано на рисунке в верхней части статьи.

Применение метода прямого возвратного цикла тривиально, поскольку существует единственный продукт пути ( C , A ) с единственным коэффициентом усиления цикла B в точке y . Таким образом, в виде матрицы эта система имеет очень компактное представление своей карты входов-выходов:

${\displaystyle T=C(1-B)^{-1}A.}$

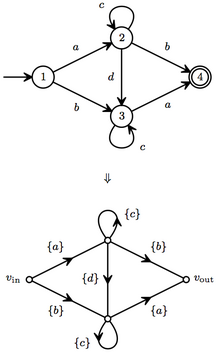
Важным типом некоммутативного графа потока сигналов является конечный автомат над алфавитом . ^{[3] [4]}${\displaystyle \Sigma }$

Последовательные соединения соответствуют конкатенации слов, которая может быть расширена до подмножеств свободного моноида . Для A , B${\displaystyle \Sigma ^{*}}$ ${\displaystyle \subseteq \Sigma ^{*}}$

${\displaystyle A\cdot B=\{ab\mid a\in A,b\in B\}.}$

Параллельные соединения соответствуют объединению множеств , которое в данном контексте часто записывается как A + B.

Наконец, самопетли естественным образом соответствуют замыканию Клини.

${\displaystyle A^{*}=\{\lambda \}+A+AA+AAA+\cdots ,}$

где пустое слово . Сходство с бесконечной геометрической прогрессией${\displaystyle \lambda }$

${\displaystyle (1-x)^{-1}=1+x+x^{2}+x^{3}\cdots ,}$

более чем поверхностно, так как выражения этой формы служат «инверсией» в этом полукольце . ^[7]

Таким образом, подмножества , построенные из конечного числа этих трех операций, можно отождествить с полукольцом регулярных выражений . Аналогично, конечные графы, ребра которых взвешены подмножествами , можно отождествить с конечными автоматами, хотя обычно эта теория начинается с одноэлементных множеств, как на рисунке.${\displaystyle \Sigma ^{*}}$${\displaystyle \Sigma ^{*}}$

Этот автомат детерминирован, поэтому мы можем однозначно перечислить пути с помощью слов. Используя метод обратного цикла, вклады путей следующие:

• путь ab , имеет узловые факторы ( c ^* , ), что дает вклад в усиление${\displaystyle \lambda }$

${\displaystyle ac^{*}b,}$

• путь ada , имеет узловые факторы ( c ^* , c ^* , ), что дает вклад в усиление${\displaystyle \lambda }$

${\displaystyle ac^{*}dc^{*}a,}$

• путь ba , имеет узловые факторы ( c ^* , ), что дает вклад в усиление${\displaystyle \lambda }$

${\displaystyle bc^{*}a.}$

Таким образом, язык , принимаемый этим автоматом (усиление его графа потока сигналов), представляет собой сумму этих терминов

${\displaystyle L=ac^{*}b+ac^{*}dc^{*}a+bc^{*}a.}$

• График потока сигналов
• Правило Мейсона
• Конечные автоматы
• Регулярные выражения

• Andaloussi, C.; Chalh, Z.; Sueur, C. (2006). «Бесконечный ноль линейных моделей графов связей, изменяющихся во времени: графические правила». Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications . pp.  2962– 2967. doi :10.1109/CACSD-CCA-ISIC.2006.4777109.
• Книга, Рональд; Эвен, Шимон; Грейбах, Шейла; Отт, Джин (1971). «Неоднозначность в графиках и выражениях» (PDF) . IEEE Transactions on Computers . 100 (2). IEEE: 149– 153. doi :10.1109/tc.1971.223204. S2CID  20676251.
• Brzozowski, JA; McCluskey, EJ Jr. (1963). «Методы построения графов потоков сигналов для диаграмм состояний последовательных цепей». IEEE Transactions on Electronic Computers (2). IEEE: 67– 76. doi :10.1109/PGEC.1963.263416.
• Грейбах, Шейла (1965). «Новая теорема нормальной формы для контекстно-свободных грамматик фразовой структуры». Журнал ACM . 12 (1). ACM: 42– 52. doi : 10.1145/321250.321254 . S2CID  12991430.
• Куич, Вернер; Саломаа, Арто (1985). Полукольца, автоматы и языки . Springer-Verlag.
• Лоренс, Чарльз С. (1964). Flowgraphs: для моделирования и анализа линейных систем . McGraw-Hill.
• Pliam, John; Lee, E. Bruce (1995). «О глобальных свойствах взаимосвязанных систем». IEEE Transactions on Circuits and Systems I: Fund. Theory and Apps . 42 (12). IEEE: 1013– 1017. doi :10.1109/81.481196.
• Ригл, Дэрил; Лин, П. М. (1972). «Матричные графы потока сигналов и оптимальный топологический метод оценки их коэффициентов усиления». Труды IEEE по теории цепей . 19 (5). IEEE: 427– 435. doi :10.1109/tct.1972.1083542.