Список уравнений механики жидкости

Часть серии статей о
Механика сплошной среды
${\displaystyle J=-D{\frac {d\varphi {dx}}}$ Законы диффузии Фика
Законы Консервации Масса Импульс Энергия Неравенства Клаузиус–Дюгем (энтропия)
Механика твёрдого тела Деформация Эластичность линейный Пластичность закон Гука Стресс Напряжение Конечная деформация Бесконечно малая деформация Совместимость Изгиб Контактная механика фрикционный Теория разрушения материалов Механика разрушения
Механика жидкости Жидкости Статика  · Динамика Принцип Архимеда  · Принцип Бернулли Уравнения Навье–Стокса Уравнение Пуазейля  · Закон Паскаля Вязкость ( Ньютоновский  · неньютоновский ) Плавучесть  · Смешивание  · Давление Жидкости Адгезия Капиллярное действие Хроматография Когезия (химия) Поверхностное натяжение Газы Атмосфера Закон Бойля Закон Шарля Комбинированный газовый закон Закон Фика Закон Гей-Люссака Закон Грэма плазма
Реология Вязкоупругость Реометрия Реометр Умные жидкости Электрореологический Магнитореологический Ферромагнитные жидкости
Ученые Бернулли Бойл Коши Чарльз Эйлер Фик Гей-Люссак Грэм Гук Ньютон Навье Нолл Паскаль Стокса Трусделл
в т е

В данной статье обобщены уравнения теории механики жидкости .

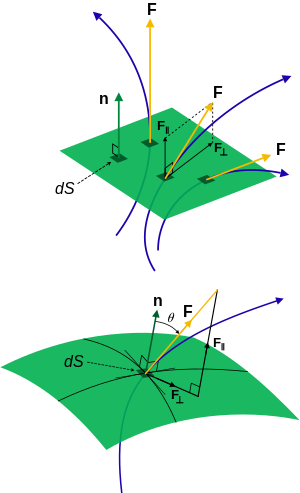
Здесь — единичный вектор в направлении потока/тока/потока.${\displaystyle \mathbf {\hat {t}} \,\!}$

Количество (общее название)	(Общий) символ/ы	Определение уравнения	Единицы СИ	Измерение
Поле вектора скорости потока	ты	${\displaystyle \mathbf {u} =\mathbf {u} \left(\mathbf {r} ,t\right)\,\!}$	мс −1	[Л][Т] −1
Поле псевдовектора скорости	ω	${\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {v} }$	с −1	[Т] −1
Объемная скорость, объемный поток	φ V (стандартного символа нет)	${\displaystyle \phi _{V}=\int _{S}\mathbf {u} \cdot \mathrm {d} \mathbf {A} \,\!}$	м 3 с −1	[Л] 3 [Т] −1
Массовый ток на единицу объема	s (стандартного символа нет)	${\displaystyle s=\mathrm {d} \rho /\mathrm {d} t\,\!}$	кг м −3 с −1	[М] [Л] −3 [Т] −1
Массовый ток, массовый расход	Я​	${\displaystyle I_{\mathrm {m} }=\mathrm {d} m/\mathrm {d} t\,\!}$	кг с −1	[М][Т] −1
Массовая плотность тока	дж м	${\displaystyle I_{\mathrm {m} }=\iint \mathbf {j} _{\mathrm {m} }\cdot \mathrm {d} \mathbf {S} \,\!}$	кг м −2 с −1	[М][Л] −2 [Т] −1
Импульсный ток	Я п	${\displaystyle I_{\mathrm {p} }=\mathrm {d} \left|\mathbf {p} \right|/\mathrm {d} t\,\!}$	кг мс −2	[М][Л][Т] −2
Плотность импульсного тока	дж п	${\displaystyle I_{\mathrm {p} }=\iint \mathbf {j} _{\mathrm {p} }\cdot \mathrm {d} \mathbf {S} }$	кг мс −2	[М][Л][Т] −2

Физическое положение	Номенклатура	Уравнения
Статика жидкости , градиент давления	г = Позиция ρ = ρ ( r ) = Плотность жидкости при гравитационном эквипотенциале, содержащем r g = g ( r ) = Напряженность гравитационного поля в точке r ∇ P = Градиент давления	${\displaystyle \nabla P=\rho \mathbf {g} \,\!}$
Уравнения плавучести	ρ f = Массовая плотность жидкости V imm = Объем тела, погруженного в жидкость F b = Выталкивающая сила F g = Сила тяжести W app = Кажущийся вес погруженного тела W = Фактический вес погруженного тела	Выталкивающая сила ${\displaystyle \mathbf {F} _{\mathrm {b} }=-\rho _{f}V_{\mathrm {imm} }\mathbf {g} =-\mathbf {F} _{\mathrm {g} }\,\!}$ Кажущийся вес ${\displaystyle \mathbf {W} _{\mathrm {app} }=\mathbf {W} -\mathbf {F} _{\mathrm {b} }\,\!}$
Уравнение Бернулли	константа p — это полное давление в точке на линии тока	${\displaystyle p+\rho u^{2}/2+\rho gy=p_{\mathrm {constant} }\,\!}$
Уравнения Эйлера	ρ = плотность массы жидкости u — вектор скорости потока E = полная объемная плотность энергии U = внутренняя энергия на единицу массы жидкости р = давление ${\displaystyle \otimes }$обозначает тензорное произведение	${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0\,\!}$ ${\displaystyle {\frac {\partial \rho {\mathbf {u} }}{\partial t}}+\nabla \cdot \left(\mathbf {u} \otimes \left(\rho \mathbf {u} \right)\right)+\nabla p=0\,\!}$ ${\displaystyle {\frac {\partial E}{\partial t}}+\nabla \cdot \left(\mathbf {u} \left(E+p\right)\right)=0\,\!}$ ${\displaystyle E=\rho \left(U+{\frac {1}{2}}\mathbf {u} ^{2}\right)\,\!}$
Конвективное ускорение		${\displaystyle \mathbf {a} =\left(\mathbf {u} \cdot \nabla \right)\mathbf {u} }$
Уравнения Навье–Стокса	T D = Девиаторный тензор напряжений ${\displaystyle \mathbf {f} }$= объемная плотность сил , действующих на жидкость ${\displaystyle \nabla }$вот оператор del .	${\displaystyle \rho \left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} \right)=-\nabla p+\nabla \cdot \mathbf {T} _{\mathrm {D} }+\mathbf {f} }$

• Определение уравнения (физическая химия)
• Список уравнений электромагнетизма
• Список уравнений классической механики
• Список уравнений гравитации
• Список уравнений в ядерной физике и физике элементарных частиц
• Список уравнений квантовой механики
• Список уравнений фотоники
• Список релятивистских уравнений
• Таблица термодинамических уравнений

• PM Whelan, MJ Hodgeson (1978). Essential Principles of Physics (2-е изд.). Джон Мюррей. ISBN 0-7195-3382-1.
• G. Woan (2010). Кембриджский справочник по физическим формулам . Cambridge University Press. ISBN 978-0-521-57507-2.
• А. Халперн (1988). 3000 решенных задач по физике, серия Шаума . McGraw Hill. ISBN 978-0-07-025734-4.
• RG Lerner , GL Trigg (2005). Энциклопедия физики (2-е изд.). VHC Publishers, Hans Warlimont, Springer. стр. 12–13. ISBN 978-0-07-025734-4.
• CB Parker (1994). McGraw Hill Encyclopaedia of Physics (2-е изд.). McGraw Hill. ISBN 0-07-051400-3.
• PA Tipler, G. Mosca (2008). Физика для ученых и инженеров: с современной физикой (6-е изд.). WH Freeman and Co. ISBN 978-1-4292-0265-7.
• LN Hand, JD Finch (2008). Аналитическая механика . Cambridge University Press. ISBN 978-0-521-57572-0.
• TB Arkill, CJ Millar (1974). Механика, вибрации и волны . Джон Мюррей. ISBN 0-7195-2882-8.
• HJ Pain (1983). Физика вибраций и волн (3-е изд.). John Wiley & Sons. ISBN 0-471-90182-2.

• LH Greenberg (1978). Физика с современными приложениями . Holt-Saunders International WB Saunders and Co. ISBN 0-7216-4247-0.
• JB Marion, WF Hornyak (1984). Принципы физики . Holt-Saunders International Saunders College. ISBN 4-8337-0195-2.
• А. Бейзер (1987). Концепции современной физики (4-е изд.). McGraw-Hill (международный). ISBN 0-07-100144-1.
• HD Young, RA Freedman (2008). University Physics – With Modern Physics (12-е изд.). Addison-Wesley (Pearson International). ISBN 978-0-321-50130-1.