Леня
Непрерывное обобщение клеточных автоматов
Образец автономной модели от Lenia.
Анимация, демонстрирующая движение планера в Лении.

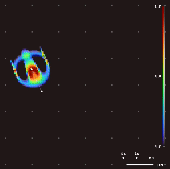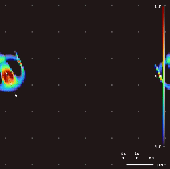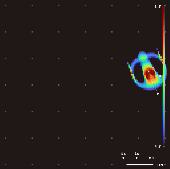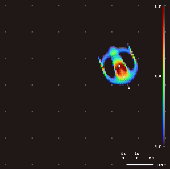
Lenia — это семейство клеточных автоматов, созданное Бертом Ван-Чаком Чаном. [1] [2] [3] Она предназначена для непрерывного обобщения игры «Жизнь» Конвея с непрерывными состояниями , пространством и временем . Вследствие ее непрерывной области высокого разрешения, сложные автономные шаблоны («формы жизни» или « космические корабли »), созданные в Lenia, описываются как отличающиеся от тех, которые появляются в других клеточных автоматах, будучи «геометрическими, метамерными , нечеткими, устойчивыми, адаптивными и генерическими правилами». [1]

Леня выиграла конкурс виртуальных существ 2018 года на конференции по генетическим и эволюционным вычислениям в Киото [4] , была удостоена почетного упоминания на премии ALIFE Art Award на конференции ALIFE 2018 в Токио [5] и получила награду за выдающуюся публикацию 2019 года от Международного общества искусственной жизни (ISAL). [6]

Правила

Итеративные обновления

Пусть будет решеткой или сеткой, содержащей набор состояний . Как и многие клеточные автоматы, Lenia обновляется итеративно; каждое выходное состояние является чистой функцией предыдущего состояния, так что Л {\displaystyle {\mathcal {L}}} С Л {\displaystyle S^{\mathcal {L}}}

Ф ( А 0 ) = А Δ т , Ф ( А Δ т ) = А 2 Δ т , … , Ф ( А т ) = А т + Δ т , … {\displaystyle \Phi (A^{0})=A^{\Delta t},\Phi (A^{\Delta t})=A^{2\Delta t},\ldots ,\Phi (A^{t})=A^{t+\Delta t},\ldots }

где — начальное состояние, а — глобальное правило , представляющее собой применение локального правила к каждому сайту . Таким образом . А 0 {\displaystyle А^{0}} Ф : С Л → С Л {\displaystyle \Phi :S^{\mathcal {L}}\rightarrow S^{\mathcal {L}}} х ∈ Л {\displaystyle \mathbf {x} \in {\cal {L}}} Ф Н ( А т ) = А т + Н Δ т {\displaystyle \Phi^{N}(A^{t})=A^{t+N\Delta t}}

Если моделирование продвигается на каждый временной шаг, то временное разрешение . Δ т {\displaystyle \Дельта t} Т = 1 Δ т {\displaystyle T={\frac {1}{\Delta t}}}

Наборы состояний

Пусть с максимальным . Это набор состояний автомата, который характеризует возможные состояния, которые могут быть найдены на каждом участке. Большее значение соответствует более высокому разрешению состояний в моделировании. Многие клеточные автоматы используют минимально возможное разрешение состояний, т. е . Lenia допускает гораздо более высокое разрешение. Обратите внимание, что фактическое значение на каждом участке не находится в , а скорее является целым кратным ; поэтому для всех мы имеем . Например, при заданном , . С = { 0 , 1 , … , П − 1 , П } {\displaystyle S=\{0,1,\ldots ,P-1,P\}} П ∈ З {\displaystyle P\in \mathbb {Z}} П {\displaystyle P} П = 1 {\displaystyle P=1} [ 0 , П ] {\displaystyle [0,P]} Δ п = 1 П {\displaystyle \Delta p={\frac {1}{P}}} А т ( х ) ∈ [ 0 , 1 ] {\displaystyle A^{t}(\mathbf {x} )\in [0,1]} х ∈ Л {\displaystyle \mathbf {x} \in {\mathcal {L}}} П = 4 {\displaystyle P=4} А т ( х ) ∈ { 0 , 0,25 , 0,5 , 0,75 , 1 } {\displaystyle \mathbf {A} ^{t}(\mathbf {x} )\in \{0,0,25,0,5,0,75,1\}}

Районы

Район Мур площадью 9 квадратов, похожий на тот, что используется в «Игре жизни».
«Шаровые» кварталы, используемые Леней.

Математически окрестности, подобные тем, что есть в Игре Жизни, могут быть представлены с помощью набора векторов положения в . Для классического района Мура, используемого в Игре Жизни, например, ; т. е. квадрат размером 3 с центром на каждом участке. Р 2 {\displaystyle \mathbb {R} ^{2}} Н = { − 1 , 0 , 1 } 2 {\displaystyle {\mathcal {N}}=\{-1,0,1\}^{2}}

В случае Лени район представляет собой шар радиуса с центром на участке, который может включать в себя и сам исходный участок. Р {\displaystyle R} Н = { х ∈ Л : ‖ х ‖ 2 ≤ Р } {\displaystyle {\mathcal {N}}=\{\mathbf {x} \in {\mathcal {L}}:\lVert \mathbf {x} \rVert _ {2}\leq R\}}

Обратите внимание, что векторы соседства не являются абсолютным положением элементов, а скорее набором относительных положений (дельт) по отношению к любому заданному месту.

Местное правило

Существуют дискретные и непрерывные варианты Lenia. Пусть будет вектором в , представляющим положение данного сайта, и будет набором сайтов, соседних с . Оба варианта включают два этапа: х {\displaystyle \mathbf {x} } Р 2 {\displaystyle \mathbb {R} ^{2}} Л {\displaystyle {\mathcal {L}}} Н {\displaystyle {\mathcal {N}}} х {\displaystyle \mathbf {x} }

  1. Использование ядра свертки для вычисления потенциального распределения . К : Н → С {\displaystyle \mathbf {K} :{\mathcal {N}}\rightarrow S} У т ( х ) = К ∗ А т ( х ) {\displaystyle \mathbf {U} ^{t}(\mathbf {x} )=\mathbf {K} *\mathbf {A} ^{t}(\mathbf {x} )}
  2. Использование карты роста для вычисления окончательного распределения роста . Г : [ 0 , 1 ] → [ − 1 , 1 ] {\displaystyle G:[0,1]\rightarrow [-1,1]} Г т ( х ) = Г ( У т ( х ) ) {\displaystyle \mathbf {G} ^{t}(\mathbf {x} )=G(\mathbf {U} ^{t}(\mathbf {x} ))}

После вычисления оно масштабируется с учетом выбранного временного разрешения и добавляется к исходному значению состояния: Здесь функция отсечения определяется как . Г т {\displaystyle \mathbf {G} ^{t}} Δ т {\displaystyle \Дельта t} А т + Δ т ( х ) = клип ( А т + Δ т Г т ( х ) , 0 , 1 ) {\displaystyle \mathbf {A} ^{t+\Delta t}(\mathbf {x} )={\text{clip}}(\mathbf {A} ^{t}+\Delta t\;\mathbf {G} ^{t}(\mathbf {x} ),\;0,\;1)} clip ⁡ ( u , a , b ) := min ( max ( u , a ) , b ) {\displaystyle \operatorname {clip} (u,a,b):=\min(\max(u,a),b)}

Локальные правила для дискретного и непрерывного Лениа определяются следующим образом:

U t ( x ) = { ∑ n ∈ N K ( n ) A t ( x + n ) Δ x 2 , discrete Lenia ∫ n ∈ N K ( n ) A t ( x + n ) d x 2 , continuous Lenia G t ( x ) = G ( U t ( x ) ) A t + Δ t ( x ) = clip ( A t ( x ) + Δ t G t ( x ) , 0 , 1 ) {\displaystyle {\begin{aligned}\mathbf {U} ^{t}(\mathbf {x} )&={\begin{cases}\sum _{\mathbf {n} \in {\mathcal {N}}}\mathbf {K(n)} \mathbf {A} ^{t}(\mathbf {x} +\mathbf {n} )\Delta x^{2},&{\text{discrete Lenia}}\\\int _{\mathbf {n} \in {\mathcal {N}}}\mathbf {K(n)} \mathbf {A} ^{t}(\mathbf {x} +\mathbf {n} )dx^{2},&{\text{continuous Lenia}}\end{cases}}\\\mathbf {G} ^{t}(\mathbf {x} )&=G(\mathbf {U} ^{t}(\mathbf {x} ))\\\mathbf {A} ^{t+\Delta t}(\mathbf {x} )&={\text{clip}}(\mathbf {A} ^{t}(\mathbf {x} )+\Delta t\;\mathbf {G} ^{t}(\mathbf {x} ),\;0,\;1)\end{aligned}}}

Генерация ядра

Оболочка ядра, скелет ядра и отображения роста для Lenia.

Существует много способов генерации ядра свертки . Конечное ядро ​​представляет собой композицию оболочки ядра и скелета ядра . K {\displaystyle \mathbf {K} } K C {\displaystyle K_{C}} K S {\displaystyle K_{S}}

Для оболочки ядра Чан приводит несколько функций, которые определены радиально . Функции оболочки ядра являются унимодальными и подчиняются ограничению (и обычно также). Примеры функций ядра включают: K C {\displaystyle K_{C}} K C ( 0 ) = K C ( 1 ) = 0 {\displaystyle K_{C}(0)=K_{C}(1)=0} K C ( 1 2 ) = 1 {\displaystyle K_{C}\left({\frac {1}{2}}\right)=1}

K C ( r ) = { exp ⁡ ( α − α 4 r ( 1 − r ) ) , exponential , α = 4 ( 4 r ( 1 − r ) ) α , polynomial , α = 4 1 [ 1 4 , 3 4 ] ( r ) , rectangular … , etc. {\displaystyle K_{C}(r)={\begin{cases}\exp \left(\alpha -{\frac {\alpha }{4r(1-r)}}\right),&{\text{exponential}},\alpha =4\\(4r(1-r))^{\alpha },&{\text{polynomial}},\alpha =4\\\mathbf {1} _{\left[{\frac {1}{4}},{\frac {3}{4}}\right]}(r),&{\text{rectangular}}\\\ldots ,&{\text{etc.}}\end{cases}}}

Здесь — индикаторная функция . 1 A ( r ) {\displaystyle \mathbf {1} _{A}(r)}

После определения оболочки ядра скелет ядра используется для его расширения и вычисления фактических значений ядра путем преобразования оболочки в ряд концентрических колец. Высота каждого кольца контролируется вектором пика ядра , где — ранг вектора параметров. Затем скелет ядра определяется как K S {\displaystyle K_{S}} β = ( β 1 , β 2 , … , β B ) ∈ [ 0 , 1 ] B {\displaystyle \beta =(\beta _{1},\beta _{2},\ldots ,\beta _{B})\in [0,1]^{B}} B {\displaystyle B} K S {\displaystyle K_{S}}

K S ( r ; β ) = β ⌊ B r ⌋ K C ( B r  mod  1 ) {\displaystyle K_{S}(r;\beta )=\beta _{\lfloor Br\rfloor }K_{C}(Br{\text{ mod }}1)}

Окончательное ядро , таким образом, K ( n ) {\displaystyle \mathbf {K} (\mathbf {n} )}

K ( n ) = K S ( ‖ n ‖ 2 ) | K S | {\displaystyle \mathbf {K} (\mathbf {n} )={\frac {K_{S}(\lVert \mathbf {n} \rVert _{2})}{|K_{S}|}}}

такой, что нормализовано так, чтобы иметь сумму элементов и (для сохранения массы ). в дискретном случае и в непрерывном случае. K {\displaystyle \mathbf {K} } 1 {\displaystyle 1} K ∗ A ∈ [ 0 , 1 ] {\displaystyle \mathbf {K} *\mathbf {A} \in [0,1]} | K S | = ∑ N K S Δ x 2 {\displaystyle |K_{S}|=\textstyle \sum _{\mathcal {N}}\displaystyle K_{S}\,\Delta x^{2}} ∫ N K S d x 2 {\displaystyle \int _{N}K_{S}\,dx^{2}}

Карты роста

Отображение роста , которое аналогично функции активации , может быть любой функцией, которая является унимодальной, немонотонной и принимает параметры . Примеры включают G : [ 0 , 1 ] → [ − 1 , 1 ] {\displaystyle G:[0,1]\rightarrow [-1,1]} μ , σ ∈ R {\displaystyle \mu ,\sigma \in \mathbb {R} }

G ( u ; μ , σ ) = { 2 exp ⁡ ( − ( u − μ ) 2 2 σ 2 ) − 1 , exponential 2 ⋅ 1 [ μ ± 3 σ ] ( u ) ( 1 − ( u − μ ) 2 9 σ 2 ) α − 1 , polynomial , α = 4 2 ⋅ 1 [ μ ± σ ] ( u ) − 1 , rectangular … , etc. {\displaystyle G(u;\mu ,\sigma )={\begin{cases}2\exp \left(-{\frac {(u-\mu )^{2}}{2\sigma ^{2}}}\right)-1,&{\text{exponential}}\\2\cdot \mathbf {1} _{[\mu \pm 3\sigma ]}(u)\left(1-{\frac {(u-\mu )^{2}}{9\sigma ^{2}}}\right)^{\alpha }-1,&{\text{polynomial}},\alpha =4\\2\cdot \mathbf {1} _{[\mu \pm \sigma ]}(u)-1,&{\text{rectangular}}\\\ldots ,&{\text{etc.}}\end{cases}}}

где — потенциальное значение, взятое из . u {\displaystyle u} U t {\displaystyle \mathbf {U} ^{t}}

Игра жизни

Игру Жизни можно рассматривать как частный случай дискретной Лении с . В этом случае ядро ​​будет прямоугольным, а функция и правило роста также будут прямоугольными, с . R = T = P = 1 {\displaystyle R=T=P=1} K C ( r ) = 1 [ 1 4 , 3 4 ] ( r ) + 1 2 1 [ 0 , 1 4 ) ( r ) {\displaystyle K_{C}(r)=\mathbf {1} _{\left[{\frac {1}{4}},{\frac {3}{4}}\right]}(r)+{\frac {1}{2}}\mathbf {1} _{\left[0,{\frac {1}{4}}\right)}(r)} μ = 0.35 , σ = 0.07 {\displaystyle \mu =0.35,\sigma =0.07}

Узоры

Некоторые из большого разнообразия «видов» в Лении.

Изменяя сверточное ядро, картирование роста и начальное состояние, в Лении было обнаружено более 400 «видов» «жизни», демонстрирующих «самоорганизацию, самовосстановление, двустороннюю и радиальную симметрию, локомотивную динамику и иногда хаотическую природу». [7] Чан создал таксономию для этих моделей. [1]

Клеточные автоматы как сверточная нейронная сеть. [8]

Другие работы отметили сильное сходство между правилами обновления клеточных автоматов и свертками. Действительно, эти работы были сосредоточены на воспроизведении клеточных автоматов с использованием упрощенных сверточных нейронных сетей . Мордвинцев и др. исследовали возникновение самовосстанавливающейся генерации шаблонов. [9] Гилпин обнаружил, что любой клеточный автомат может быть представлен как сверточная нейронная сеть, и обучил нейронные сети воспроизводить существующие клеточные автоматы [8]

В этом свете клеточные автоматы можно рассматривать как особый случай рекуррентных сверточных нейронных сетей. Правило обновления Lenia можно также рассматривать как однослойную свертку («потенциальное поле» ) с функцией активации («отображение роста» ). Однако Lenia использует гораздо большие, фиксированные ядра и не обучается с помощью градиентного спуска. K {\displaystyle \mathbf {K} } G {\displaystyle G}

Смотрите также

  • Репозиторий Github для Lenia
  • Сайт Чана для Лени
  • Приглашенный семинар в Стэнфорде, который провел Чан

Ссылки

  1. ^ abc Chan, Bert Wang-Chak (2019-10-15). «Lenia: Biology of Artificial Life». Complex Systems . 99999 (3): 251– 286. arXiv : 1812.05433 . doi : 10.25088/ComplexSystems.28.3.251.
  2. ^ "Ления". chakazul.github.io . Проверено 12 октября 2021 г.
  3. ^ Робертс, Сиобхан (28.12.2020). «Последние уроки игры Джона Конвея в жизнь». The New York Times . ISSN  0362-4331 . Получено 13.10.2021 .
  4. ^ "Конкурс виртуальных существ". virtualcreatures.github.io . Получено 2021-10-12 .
  5. ^ "ALife Art Award 2018". ALIFE Art Award 2018 . Получено 2021-10-12 .
  6. ^ «Премии ISAL 2020: победители».
  7. ^ "Ления". chakazul.github.io . Проверено 13 октября 2021 г.
  8. ^ ab Gilpin, William (2019-09-04). "Клеточные автоматы как сверточные нейронные сети". Physical Review E. 100 ( 3): 032402. arXiv : 1809.02942 . doi : 10.1103/PhysRevE.100.032402 . ISSN  2470-0045.
  9. ^ Мордвинцев, Александр; Рандаццо, Этторе; Никлассон, Эйвинд; Левин, Майкл (11 февраля 2020 г.). «Выращивание нейроклеточных автоматов». Дистиллировать . 5 (2): е23. дои : 10.23915/distill.00023 . ISSN  2476-0757.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Lenia&oldid=1260624773"