Ядро (обработка изображений)
Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . ( Октябрь 2023 ) |
В обработке изображений ядро , матрица свертки или маска — это небольшая матрица, используемая для размытия, резкости, тиснения, обнаружения краев и многого другого. Это достигается путем выполнения свертки между ядром и изображением . Или, проще говоря, когда каждый пиксель в выходном изображении является функцией соседних пикселей (включая себя) во входном изображении, ядро — это эта функция.
Подробности
Общее выражение свертки:
где — отфильтрованное изображение, — исходное изображение, — ядро фильтра. Каждый элемент ядра фильтра рассматривается с помощью и .
В зависимости от значений элементов ядро может вызывать широкий спектр эффектов:
| Операция | Ядро ω | Результат изображения g(x,y) |
|---|---|---|
| Личность |  | |
| Обнаружение гребня или края | 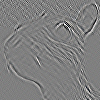 | |
 | ||
| Резкость |  | |
| Размытие рамки ( нормализованное ) |  | |
| Размытие по Гауссу 3 × 3 (приблизительно) |  | |
| Размытие по Гауссу 5 × 5 (приблизительно) |  | |
| Нерезкое маскирование 5 × 5. Основано на гауссовом размытии со значением 1 и порогом 0 (без маски изображения ). |  |
Выше приведены лишь несколько примеров эффектов, которых можно добиться путем свертывания ядер и изображений.
Источник
Начало координат — это положение ядра, которое находится выше (концептуально) текущего выходного пикселя. Это может быть вне фактического ядра, хотя обычно соответствует одному из элементов ядра. Для симметричного ядра начало координат обычно является центральным элементом.
Свертка
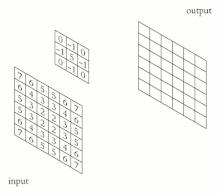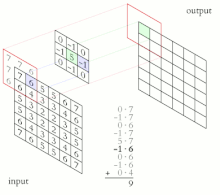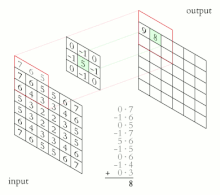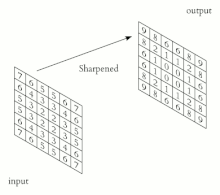
Свертка — это процесс добавления каждого элемента изображения к его локальным соседям, взвешенным ядром. Это связано с формой математической свертки . Выполняемая матричная операция — свертка — не является традиционным умножением матриц, несмотря на то, что она также обозначается *.
Например, если у нас есть две матрицы размером три на три, первая — ядро, а вторая — часть изображения, свертка — это процесс переворачивания строк и столбцов ядра и умножения локально похожих записей и суммирования. Элемент с координатами [2, 2] (то есть центральный элемент) результирующего изображения будет взвешенной комбинацией всех записей матрицы изображения с весами, заданными ядром:
Остальные записи будут взвешены аналогичным образом, где мы размещаем центр ядра на каждой из граничных точек изображения и вычисляем взвешенную сумму.
Значения заданного пикселя в выходном изображении вычисляются путем умножения каждого значения ядра на соответствующие значения пикселей входного изображения. Это можно описать алгоритмически с помощью следующего псевдокода:
для каждой строки изображения во входном изображении : для каждого пикселя в строке изображения : установить аккумулятор на ноль для каждой строки ядра в ядре : для каждого элемента в строке ядра : если позиция элемента соответствует* позиции пикселя , то умножьте значение элемента, соответствующее*, на значение пикселя, добавьте результат в аккумулятор endif установить пиксель выходного изображения в аккумулятор
- *соответствующие пиксели входного изображения находятся относительно начала координат ядра.
Если ядро симметрично, то поместите центр (начало координат) ядра на текущий пиксель. Ядро будет перекрывать соседние пиксели вокруг начала координат. Каждый элемент ядра должен быть умножен на значение пикселя, с которым он перекрывается, и все полученные значения должны быть просуммированы. Эта результирующая сумма будет новым значением для текущего пикселя, который в данный момент перекрывается с центром ядра.
Если ядро не симметрично, его необходимо перевернуть как вокруг горизонтальной, так и вокруг вертикальной оси перед вычислением свертки, как указано выше. [1]
Общая форма матричной свертки имеет вид
Обработка кромок

Свертка ядра обычно требует значений из пикселей за пределами границ изображения. Существует множество методов обработки краев изображения.
- Продлевать
- Ближайшие граничные пиксели концептуально расширяются настолько, насколько это необходимо для предоставления значений для свертки. Угловые пиксели расширяются в 90° клинья. Другие граничные пиксели расширяются в линии.
- Сворачивать
- Изображение концептуально обернуто (или разбито на фрагменты), а значения берутся с противоположного края или угла.
- Зеркало
- Изображение концептуально зеркально отражается по краям. Например, попытка прочитать пиксель на 3 единицы снаружи края вместо этого прочитает пиксель на 3 единицы внутри края.
- Обрезать / Избегать наложения
- Любой пиксель в выходном изображении, который требует значений из-за края, пропускается. Этот метод может привести к тому, что выходное изображение будет немного меньше, а края будут обрезаны. Переместите ядро так, чтобы значения из-за пределов изображения никогда не требовались. Машинное обучение в основном использует этот подход. Пример: размер ядра 10x10, размер изображения 32x32, результирующее изображение 23x23.
- Урожай зерна
- Любой пиксель в ядре, выходящий за пределы входного изображения, не используется, а нормализация корректируется для компенсации.
- Постоянный
- Использовать постоянное значение для пикселей за пределами изображения. Обычно используется черный или иногда серый цвет. Обычно это зависит от приложения.
Нормализация
Нормализация определяется как деление каждого элемента в ядре на сумму всех элементов ядра, так что сумма элементов нормализованного ядра равна единице. Это гарантирует, что средний пиксель в измененном изображении будет таким же ярким, как и средний пиксель в исходном изображении.
Оптимизация
Алгоритмы быстрой свертки включают в себя:
- разделяемая свертка
Разделяемая свертка
Двумерная свертка с ядром M × N требует M × N умножений для каждого образца (пикселя). Если ядро разделимо, то вычисление можно сократить до M + N умножений. Использование разделимых сверток может значительно сократить вычисление, выполняя одномерную свертку дважды вместо одной двумерной свертки. [2]
Выполнение
Вот конкретная реализация свертки, выполненная с использованием языка шейдеров GLSL :
// автор: csblo // Работа сделана просто консультируясь: // https://en.wikipedia.org/wiki/Kernel_(image_processing)// Определяем ядра #define identity mat3(0, 0, 0, 0, 1, 0, 0, 0, 0) #define edge0 mat3(1, 0, -1, 0, 0, 0, -1, 0, 1) #define edge1 mat3(0, 1, 0, 1, -4, 1, 0, 1, 0) #define edge2 mat3(-1, -1, -1, -1, 8, -1, -1, -1, -1) #define sharpen mat3(0, -1, 0, -1, 5, -1, 0, -1, 0) #define box_blur mat3(1, 1, 1, 1, 1, 1, 1, 1, 1) * 0.1111 #define gaussian_blur mat3(1, 2, 1, 2, 4, 2, 1, 2, 1) * 0,0625 #определить мат тиснения3(-2, -1, 0, -1, 1, 1, 0, 1, 2)// Найти координату элемента матрицы из индекса vec2 kpos ( int index ) { return vec2 [ 9 ] ( vec2 ( - 1 , - 1 ), vec2 ( 0 , - 1 ), vec2 ( 1 , - 1 ), vec2 ( - 1 , 0 ), vec2 ( 0 , 0 ), vec2 ( 1 , 0 ), vec2 ( - 1 , 1 ), vec2 ( 0 , 1 ), vec2 ( 1 , 1 ) )[ index ] / iResolution . xy ; } // Извлечь область размером 3x3 из сэмплера, центрированную в uv // сэмплер: текстурный сэмплер // uv: текущие координаты на сэмплере // вернуть: массив mat3, каждый индекс которого соответствует цветовому каналу mat3 [ 3 ] region3x3 ( sampler2D sampler , vec2 uv ) { // Создать каждый пиксель для области vec4 [ 9 ] region ; for ( int i = 0 ; i < 9 ; i ++ ) region [ i ] = texture ( sampler , uv + kpos ( i )); // Создаем область 3x3 с 3 цветовыми каналами (красный, зеленый, синий) mat3 [ 3 ] mRegion ; for ( int i = 0 ; i < 3 ; i ++ ) mRegion [ i ] = mat3 ( region [ 0 ][ i ], region [ 1 ] [ i ], region [ 2 ][ i ], region [ 3 ][ i ], region [ 4 ][ i ], region [ 5 ][ i ], region [ 6 ][ i ], region [ 7 ][ i ], region [ 8 ][ i ] ); return mRegion ; } // Свернуть текстуру с ядром // kernel: ядро, используемое для свертки // sampler: сэмплер текстуры // uv: текущие координаты сэмплера vec3 convolution ( mat3 kernel , sampler2D sampler , vec2 uv ) { vec3 fragment ; // Извлечь область 3x3 с центром в uv mat3 [ 3 ] region = region3x3 ( sampler , uv ); // для каждого цветового канала области for ( int i = 0 ; i < 3 ; i ++ ) { // получить канал области mat3 rc = region [ i ]; // покомпонентное умножение ядра на канал области mat3 c = matrixCompMult ( kernel , rc ); // сложить каждый компонент матрицы float r = c [ 0 ][ 0 ] + c [ 1 ][ 0 ] + c [ 2 ][ 0 ] + c [ 0 ][ 1 ] + c [ 1 ][ 1 ] + c [ 2 ][ 1 ] + c [ 0 ][ 2 ] + c [ 1 ][ 2 ] + c [ 2 ][ 2 ]; // для фрагмента на канале i установить результат fragment [ i ] = r ; } return fragment ; } void mainImage ( out vec4 fragColor , in vec2 fragCoord ) { // Нормализованные координаты пикселей (от 0 до 1) vec2 uv = fragCoord / iResolution . xy ; // Свертка ядра с текстурой vec3 col = convolution ( emboss , iChannel0 , uv ); // Вывод на экран fragColor = vec4 ( col , 1.0 ); } Смотрите также
Ссылки
- ^ «Пример двумерной свертки».
- ^ "Convolution". www.songho.ca . Получено 2022-11-19 .
Источники
- Людвиг, Джейми (nd). Свертка изображений (PDF) . Портлендский государственный университет.
- Lecarme, Olivier; Delvare, Karine (январь 2013). Книга GIMP: Полное руководство почти по всему . No Starch Press. стр. 429. ISBN 978-1593273835.
- Gumster, Jason van; Shimonski, Robert (март 2012). GIMP Bible . John Wiley & Sons. стр. 438–442. ISBN 978-0470523971.
- Шапиро, Линда Г.; Стокман, Джордж К. (февраль 2001 г.). Компьютерное зрение . Prentice Hall. стр. 53–54. ISBN 978-0130307965.
Внешние ссылки
- Реализация 2D свертки на ПЛИС
- Руководство по программированию vImage: выполнение операций свертки
- Обработка изображений с использованием 2D-свертки
- Программа обработки изображений GNU - Руководство пользователя - 8.2. Матрица свертки
- Демонстрация GLSL ядер свертки 3x3
- Полный проект с открытым исходным кодом на C++















![{\displaystyle \left({\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}}*{\begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix}}\right)[2,2]=(i\cdot 1)+(h\cdot 2)+(g\cdot 3)+(f\cdot 4)+(e\cdot 5)+(d\cdot 6)+(c\cdot 7)+(b\cdot 8)+(a\cdot 9).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/570600fdeed436d98626278f22bf034ff5ab5162)
