Кан волокнистый

В математике комплексы Кана и расслоения Кана являются частью теории симплициальных множеств . Расслоения Кана являются расслоениями стандартной модельной категории структуры на симплициальных множествах и поэтому имеют фундаментальное значение. Комплексы Кана являются фибрантными объектами в этой модельной категории. Название дано в честь Дэниела Кана .

Для каждого n  ≥ 0 напомним, что стандартный -симплекс${\displaystyle n}$ , , является представимым симплициальным множеством${\displaystyle \Дельта ^{n}}$

${\displaystyle \Delta ^{n}(i)=\mathrm {Hom} _ {\mathbf {\Delta } }([i],[n])}$

Применение функтора геометрической реализации к этому симплициальному множеству дает пространство, гомеоморфное топологическому стандарту -симплексу${\displaystyle n}$ : выпуклое подпространство, состоящее из всех точек, координаты которых неотрицательны и в сумме дают 1.${\displaystyle \mathbb {R} ^{n+1}}$${\displaystyle (t_{0},\точки ,t_{n})}$

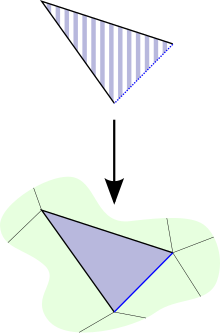
Для каждого k  ≤  n , это имеет подкомплекс , k -й рог внутри , соответствующий границе n -симплекса, с удаленной k -й гранью. Это может быть формально определено различными способами, например, объединением образов n карт, соответствующих всем остальным граням . ^[1] Рога формы, расположенные внутри, выглядят как черная V в верхней части соседнего изображения. Если — симплициальное множество, то отображения${\displaystyle \Lambda _ {k}^{n}}$${\displaystyle \Дельта ^{n}}$${\displaystyle \Дельта ^{n-1}\rightarrow \Дельта ^{n}}$${\displaystyle \Дельта ^{n}}$${\displaystyle \Lambda _{k}^{2}}$${\displaystyle \Дельта ^{2}}$${\displaystyle X}$

${\displaystyle s:\Лямбда _{k}^{n}\to X}$

соответствуют коллекциям -симплексов, удовлетворяющих условию совместимости, по одному для каждого . Явно это условие можно записать следующим образом. Запишите -симплексы в виде списка и потребуйте, чтобы${\displaystyle n}$ ${\displaystyle (n-1)}$${\displaystyle 0\leq k\leq n-1}$${\displaystyle (n-1)}$${\displaystyle (s_{0},\точки,s_{k-1},s_{k+1},\точки,s_{n})}$

${\displaystyle d_{i}s_{j}=d_{j-1}s_{i}\,}$для всех с . ^[2]${\displaystyle я<j}$${\displaystyle i,j\neq k}$

Эти условия выполняются для -симплексов, сидящих внутри .${\displaystyle (n-1)}$${\displaystyle \Lambda _ {k}^{n}}$${\displaystyle \Дельта ^{n}}$

Карта симплициальных множеств является расслоением Кана , если для любых и , и для любых отображений и таких, что (где — включение в ), существует отображение такое, что и . Сформулированное таким образом определение очень похоже на определение расслоений в топологии (см. также свойство подъема гомотопии ), откуда и произошло название «расслоение».${\displaystyle f:X\rightarrow Y}$${\displaystyle n\geq 1}$${\displaystyle 0\leq k\leq n}$${\displaystyle s:\Лямбда _{k}^{n}\rightarrow X}$${\displaystyle y:\Delta ^{n}\rightarrow Y\,}$${\displaystyle f\circ s=y\circ i}$${\displaystyle я}$${\displaystyle \Lambda _ {k}^{n}}$${\displaystyle \Дельта ^{n}}$${\displaystyle x:\Delta ^{n}\rightarrow X}$${\displaystyle s=x\circ i}$${\displaystyle y=f\circ x}$

Используя соответствие между -симплексами симплициального множества и морфизмами (следствие леммы Йонеды ), это определение можно записать в терминах симплексов. Изображение карты можно рассматривать как рог, как описано выше. Запрос на то, чтобы факторы через соответствовал требованию, чтобы существовал -симплекс, в чьих гранях содержится рог из (вместе с одной другой гранью). Тогда требуемая карта соответствует симплексу, в чьих гранях содержится рог из . Диаграмма справа является примером в двух измерениях. Поскольку черная V на нижней диаграмме заполнена синим -симплексом, если черная V выше отображается на нее, то полосатый синий -симплекс должен существовать вместе с пунктирным синим -симплексом, отображаясь вниз очевидным образом. ^[3]${\displaystyle n}$${\displaystyle X}$${\displaystyle \Delta ^{n}\to X}$${\displaystyle fs:\Lambda _{k}^{n}\to Y}$${\displaystyle fs}$${\displaystyle yi}$${\displaystyle n}$${\displaystyle Y}$${\displaystyle fs}$${\displaystyle x:\Delta ^{n}\to X}$${\displaystyle X}$${\displaystyle s}$${\displaystyle 2}$${\displaystyle 2}$${\displaystyle 1}$

Симплициальное множество называется комплексом Кана, если отображение из , одноточечного симплициального множества, является расслоением Кана. В категории моделей для симплициальных множеств является конечным объектом, и поэтому комплекс Кана в точности совпадает с фибрантным объектом . Эквивалентно это можно сформулировать так: если каждое отображение из рога имеет расширение до , то есть существует подъем такой, что${\displaystyle X}$${\displaystyle X\to \{*\}}$${\displaystyle \{*\}}$${\displaystyle \alpha :\Lambda _{k}^{n}\to X}$${\displaystyle \Delta ^{n}}$${\displaystyle {\tilde {\alpha }}:\Delta ^{n}\to X}$

${\displaystyle \alpha ={\tilde {\alpha }}\circ \iota }$

для отображения включения , то есть комплекс Кан. Наоборот, каждый комплекс Кан обладает этим свойством, следовательно, это дает простое техническое условие для комплекса Кан.${\displaystyle \iota :\Lambda _{k}^{n}\hookrightarrow \Delta ^{n}}$${\displaystyle X}$

Важный пример можно найти в конструкции сингулярных симплексов, используемых для определения сингулярных гомологий , называемых сингулярным функтором ^{[4] стр. 7}

${\displaystyle S:{\text{Top}}\to s{\text{Sets}}}$.

Для данного пространства определим сингулярный -симплекс пространства X как непрерывное отображение из стандартного топологического -симплекса (как описано выше) в ,${\displaystyle X}$${\displaystyle n}$${\displaystyle n}$${\displaystyle X}$

${\displaystyle f:\Delta _{n}\to X}$

Принимая набор этих карт за все неотрицательные, получаем градуированный набор,${\displaystyle n}$

${\displaystyle S(X)=\coprod _{n}S_{n}(X)}$.

Чтобы превратить это в симплициальный набор, определим карты граней следующим образом:${\displaystyle d_{i}:S_{n}(X)\to S_{n-1}(X)}$

${\displaystyle (d_{i}f)(t_{0},\dots ,t_{n-1})=f(t_{0},\dots ,t_{i-1},0,t_{i},\dots ,t_{n-1})\,}$

и карты вырождения по${\displaystyle s_{i}:S_{n}(X)\to S_{n+1}(X)}$

${\displaystyle (s_{i}f)(t_{0},\dots ,t_{n+1})=f(t_{0},\dots ,t_{i-1},t_{i}+t_{i+1},t_{i+2},\dots ,t_{n+1})\,}$.

Поскольку объединение любых граней является сильным деформационным ретрактом , любая непрерывная функция, определенная на этих гранях, может быть продолжена до , что показывает, что является комплексом Кана. ^[5]${\displaystyle n+1}$${\displaystyle \Delta _{n+1}}$${\displaystyle \Delta _{n+1}}$${\displaystyle \Delta _{n+1}}$${\displaystyle S(X)}$

Стоит отметить, что сингулярный функтор является правым сопряженным к функтору геометрической реализации

${\displaystyle |\cdot |:s{\text{Sets}}\to {\text{Top}}}$

давая изоморфизм

${\displaystyle {\text{Hom}}_{\text{Top}}(|X|,Y)\cong {\text{Hom}}_{s{\text{Sets}}}(X,S(Y))}$

Можно показать, что симплициальное множество, лежащее в основе симплициальной группы, всегда фибрантно ^{[4] стр. 12.} В частности, для симплициальной абелевой группы ее геометрическая реализация гомотопически эквивалентна произведению пространств Эйленберга-Маклана

${\displaystyle \prod _{i\in I}K(A_{i},n_{i})}$

В частности, это включает классификацию пространств . Так что пространства , , и бесконечные линзовые пространства соответствуют комплексам Кана некоторого симплициального множества. Фактически, это множество может быть построено явно с использованием соответствия Дольда–Кана цепного комплекса и взятия базового симплициального множества симплициальной абелевой группы.${\displaystyle S^{1}\simeq K(\mathbb {Z} ,1)}$${\displaystyle \mathbb {CP} ^{\infty }\simeq K(\mathbb {Z} ,2)}$${\displaystyle L_{q}^{\infty }\simeq K(\mathbb {Z} /q,2)}$

Другим важным источником примеров являются симплициальные множества, связанные с малым группоидом . Это определяется как геометрическая реализация симплициального множества и обычно обозначается . Мы могли бы также заменить на бесконечный группоид. Предполагается, что гомотопическая категория геометрических реализаций бесконечных группоидов эквивалентна гомотопической категории гомотопических типов. Это называется гипотезой гомотопии.${\displaystyle {\mathcal {G}}}$${\displaystyle [\Delta ^{op},{\mathcal {G}}]}$${\displaystyle B{\mathcal {G}}}$${\displaystyle {\mathcal {G}}}$

Оказывается, стандартный -симплекс не является комплексом Кана ^{[6] стр} . 38. Построение контрпримера в общем случае можно найти, посмотрев на пример малой размерности, скажем . Взяв карту, посылающую${\displaystyle n}$${\displaystyle \Delta ^{n}}$${\displaystyle \Delta ^{1}}$${\displaystyle \Lambda _{0}^{2}\to \Delta ^{1}}$

${\displaystyle {\begin{matrix}[0,2]\mapsto [0,0]&[0,1]\mapsto [0,1]\end{matrix}}}$

дает контрпример, поскольку он не может быть расширен до карты , поскольку карты должны быть сохраняющими порядок. Если бы была карта, она должна была бы отправить${\displaystyle \Delta ^{2}\to \Delta ^{1}}$

${\displaystyle {\begin{aligned}0\mapsto 0\\1\mapsto 1\\2\mapsto 0\end{aligned}}}$

но это не карта симплициальных множеств.

Для симплициальных множеств существует связанное симплициальное множество, называемое комплексом функций , где симплексы определяются как${\displaystyle X,Y}$ ${\displaystyle {\textbf {Hom}}(X,Y)}$

${\displaystyle {\textbf {Hom}}_{n}(X,Y)={\text{Hom}}_{s{\text{Sets}}}(X\times \Delta ^{n},Y)}$

и для ординального отображения существует индуцированное отображение${\displaystyle \theta :[m]\to [n]}$

${\displaystyle \theta ^{*}:{\textbf {Hom}}(X,Y)_{n}\to {\textbf {Hom}}(X,Y)_{m}}$

(поскольку первый фактор Hom контравариантен), определяемый путем отправки карты в композицию${\displaystyle f:X\times \Delta ^{n}\to Y}$

${\displaystyle X\times \Delta ^{m}\xrightarrow {1\times \theta } X\times \Delta ^{n}\xrightarrow {f} Y}$

Этот комплекс имеет следующий показательный закон симплициальных множеств

${\displaystyle {\text{ev}}_{*}:{\text{Hom}}_{s{\text{Sets}}}(K,{\textbf {Hom}}(X,Y))\to {\text{Hom}}_{s{\text{Sets}}}(X\times K,Y)}$

который отправляет карту в составную карту${\displaystyle f:K\to {\textbf {Hom}}(X,Y)}$

${\displaystyle X\times K\xrightarrow {1\times g} X\times {\textbf {Hom}}(X,Y)\xrightarrow {ev} Y}$

где для поднятого до n-симплекса . ^${\displaystyle ev(x,f)=f(x,\iota _{n})}$${\displaystyle \iota _{n}\in {\text{Hom}}_{\Delta }([n],[n])}$${\displaystyle \Delta ^{n}}$

При наличии расслоения (Кан) и включения симплициальных множеств существует расслоение ^{[4] стр. 21}${\displaystyle p:X\to Y}$${\displaystyle i:K\hookrightarrow L}$

${\displaystyle {\textbf {Hom}}(L,X)\xrightarrow {(i^{*},p_{*})} {\textbf {Hom}}(K,X)\times _{{\textbf {Hom}}(K,Y)}{\textbf {Hom}}(L,Y)}$

(где находится в функциональном комплексе в категории симплициальных множеств), индуцированном из коммутативной диаграммы${\displaystyle {\textbf {Hom}}}$

${\displaystyle {\begin{matrix}{\textbf {Hom}}(L,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(L,Y)\\i^{*}\downarrow &&\downarrow i^{*}\\{\textbf {Hom}}(K,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(K,Y)\end{matrix}}}$

где — это карта pull-back, заданная предкомпозицией, а — это карта pushforward, заданная посткомпозицией. В частности, предыдущее расслоение подразумевает и — это расслоения.${\displaystyle i^{*}}$${\displaystyle p_{*}}$${\displaystyle p_{*}:{\textbf {Hom}}(L,X)\to {\textbf {Hom}}(L,Y)}$${\displaystyle i^{*}:{\textbf {Hom}}(L,Y)\to {\textbf {Hom}}(K,Y)}$

Гомотопические группы фибрантного симплициального множества могут быть определены комбинаторно, с использованием рогов, способом, который согласуется с гомотопическими группами топологического пространства, которое его реализует. Для комплекса Кана и вершины , как множество определяется как множество карт симплициальных множеств, вписывающихся в некоторую коммутативную диаграмму:${\displaystyle X}$${\displaystyle x:\Delta ^{0}\to X}$${\displaystyle \pi _{n}(X,x)}$${\displaystyle \alpha :\Delta ^{n}\to X}$

${\displaystyle \pi _{n}(X,x)=\left\{\alpha :\Delta ^{n}\to X:{\begin{matrix}\Delta ^{n}&{\overset {\alpha }{\to }}&X\\\uparrow &&\uparrow x\\\partial \Delta ^{n}&\to &\Delta ^{0}\end{matrix}}\right\}}$

Обратите внимание, что факт отображения в точку эквивалентен определению сферы как частного для стандартного единичного шара.${\displaystyle \partial \Delta ^{n}}$${\displaystyle S^{n}}$${\displaystyle B^{n}/\partial B^{n}}$

${\displaystyle B^{n}=\{x\in \mathbb {R} ^{n}:||x||_{eu}\leq 1\}}$

Определение структуры группы требует немного больше работы. По сути, для двух карт имеется ассоциированный -симплекс , который дает их сложение. Эта карта хорошо определена с точностью до симплициальных гомотопических классов карт, что дает структуру группы. Более того, группы являются абелевыми для . Для она определяется как гомотопические классы вершинных карт .${\displaystyle \alpha ,\beta :\Delta ^{n}\to X}$${\displaystyle (n+1)}$${\displaystyle \omega :\Delta ^{n+1}\to X}$${\displaystyle d_{n}\omega :\Delta ^{n}\to X}$${\displaystyle \pi _{n}(X,x)}$${\displaystyle n\geq 2}$${\displaystyle \pi _{0}(X)}$${\displaystyle [x]}$${\displaystyle x:\Delta ^{0}\to X}$

Используя модельные категории, любое симплициальное множество имеет фибрантную замену , которая гомотопически эквивалентна в гомотопической категории симплициальных множеств. Тогда гомотопические группы можно определить как${\displaystyle X}$${\displaystyle {\hat {X}}}$${\displaystyle X}$${\displaystyle X}$

${\displaystyle \pi _{n}(X,x):=\pi _{n}({\hat {X}},{\hat {x}})}$

где — это подъем в . Эти фибрантные замены можно рассматривать как топологический аналог разрешений цепного комплекса (например, проективное разрешение или плоское разрешение ).${\displaystyle {\hat {x}}}$${\displaystyle x:\Delta ^{0}\to X}$${\displaystyle {\hat {X}}}$

• Категория модели
• Симплициальная гомотопическая теория
• Упрощенно обогащенная категория
• Слабый комплекс Кана (также называемый квазикатегорией, ∞-категорией)
• ∞-группоид
• Расслоение симплициальных множеств

• Элементарное иллюстрированное введение в симплициальные множества

• Goerss, Paul G.; Jardine, John F. (1999). Симплициальная гомотопическая теория . Базель: Birkhäuser Basel. doi :10.1007/978-3-0348-8707-6. ISBN 978-3-0348-9737-2. МР  1711612.
• Мэй, Дж. Питер (1992) [1967]. Симплициальные объекты в алгебраической топологии . Чикагские лекции по математике. Чикаго, Иллинойс: Издательство Чикагского университета . ISBN 0-226-51180-4. МР  1206474.