Кампила Евдокса

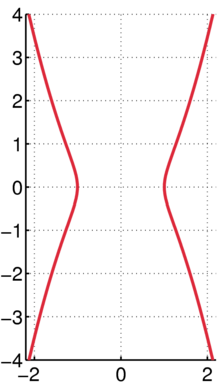
Кампила Евдокса ( греч . καμπύλη [γραμμή], что означает просто «изогнутая [линия], кривая») представляет собой кривую с декартовым уравнением

${\displaystyle x^{4}=a^{2}(x^{2}+y^{2}),}$

из которого решение x = y = 0 исключено.

В полярных координатах Кампиле имеет уравнение

${\displaystyle r=a\сек ^{2}\тета .}$

Эквивалентно, он имеет параметрическое представление как

${\displaystyle x=a\sec(t),\quad y=a\tan(t)\sec(t).}$

Эту четвертую кривую изучал греческий астроном и математик Евдокс Книдский (ок. 408 г. до н.э. – ок. 347 г. до н.э.) в связи с классической задачей удвоения куба .

Кампиле симметричен относительно осей x и y . Он пересекает ось x в точке (± a ,0). Он имеет точки перегиба в

${\displaystyle \left(\pm a{\frac {\sqrt {6}}{2}},\pm a{\frac {\sqrt {3}}{2}}\right)}$

(четыре перегиба, по одному в каждом квадранте). Верхняя половина кривой асимптотически соответствует , и фактически может быть записана как${\displaystyle x^{2}/aa/2}$${\displaystyle x\to \infty }$

${\displaystyle y={\frac {x^{2}}{a}}{\sqrt {1-{\frac {a^{2}}{x^{2}}}}}={\frac {x^{2}}{a}}-{\frac {a}{2}}\sum _{n=0}^{\infty }C_{n}\left({\frac {a}{2x}}\right)^{2n},}$

где

${\displaystyle C_{n}={\frac {1}{n+1}}{\binom {2n}{n}}}$

- это -ое каталонское число .${\displaystyle n}$

• Список кривых

• J. Dennis Lawrence (1972). Каталог специальных плоских кривых . Dover Publications. стр. 141–142. ISBN 0-486-60288-5.

• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Кампила Евдокса», Архив истории математики Мактьютора , Университет Сент-Эндрюс
• Вайсштейн, Эрик В. «Кампила Евдокса». MathWorld .