Счетчик колец
Кольцевой счетчик — это тип счетчика, состоящий из триггеров, соединенных в сдвиговый регистр , при этом выход последнего триггера подается на вход первого, образуя «кольцевую» или «кольцевую» структуру.
Существует два типа счетчиков колец:
- Прямой кольцевой счетчик , также известный как счетчик с одним срабатыванием , соединяет выход последнего регистра сдвига с входом первого регистра сдвига и циркулирует по кольцу один бит единицы (или нуля).
- Счетчик с витым кольцом , также называемый счетчиком с переключающимся хвостом , счетчиком шагающего кольца , счетчиком Джонсона или счетчиком Мёбиуса , соединяет дополнение выхода последнего регистра сдвига со входом первого регистра и циркулирует по кольцу поток единиц, за которыми следуют нули.
Четырехбитовые последовательности кольцевого счетчика
| Прямой кольцевой счетчик | Счетчик Джонсона | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Состояние | Q0 | Q1 | Q2 | Q3 | Состояние | Q0 | Q1 | Q2 | Q3 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 2 | 1 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 4 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 5 | 0 | 1 | 1 | 1 | |
| 2 | 0 | 0 | 1 | 0 | 6 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Характеристики
Кольцевые счетчики часто используются в аппаратном проектировании (например, проектировании ASIC и FPGA ) для создания конечных автоматов . Двоичный счетчик потребовал бы схему сумматора , которая существенно сложнее, чем кольцевой счетчик, и имеет большую задержку распространения по мере увеличения числа бит, тогда как задержка распространения кольцевого счетчика будет почти постоянной независимо от числа бит в коде.
Прямые и скрученные формы имеют разные свойства, а также относительные преимущества и недостатки.
Общим недостатком кольцевых счетчиков является то, что они являются кодами с меньшей плотностью, чем обычные двоичные кодировки номеров состояний. Двоичный счетчик может представлять 2 N состояний, где N — число бит в коде, тогда как прямой кольцевой счетчик может представлять только N состояний, а счетчик Джонсона может представлять только 2 N состояний. Это может быть важным соображением в аппаратных реализациях, где регистры дороже комбинационной логики.
Счетчики Джонсона иногда предпочитают, потому что они предлагают вдвое больше состояний счета из того же числа регистров сдвига, и потому что они способны самоинициализироваться из состояния всех нулей, не требуя, чтобы первый бит счета был введен извне при запуске. Счетчик Джонсона генерирует код, в котором соседние состояния отличаются только одним битом (то есть имеют расстояние Хэмминга 1), как в коде Грея , что может быть полезно, если битовая комбинация будет асинхронно сэмплироваться. [1]
Когда требуется полностью декодированное или одноточечное представление состояния счетчика, как в некоторых контроллерах последовательности, предпочтительным является прямой кольцевой счетчик. Свойство одноточечного действия означает, что набор кодов разделен минимальным расстоянием Хэмминга 2, [2], поэтому любая однобитовая ошибка может быть обнаружена (как и любой шаблон ошибки, отличный от включения одного бита и выключения одного бита).
Иногда используются двунаправленные регистры сдвига (использующие мультиплексоры для получения входных данных для каждого триггера от его левого или правого соседа), так что можно создавать двунаправленные или кольцевые счетчики вверх-вниз. [3]
Логические схемы
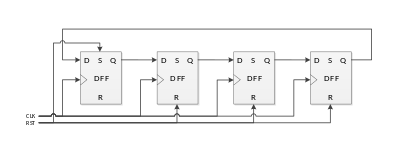
Прямой кольцевой счетчик имеет логическую структуру, показанную здесь:
Вместо того чтобы линия сброса устанавливала начальный одноконтактный шаблон, прямое кольцо иногда делается самоинициализирующимся с помощью распределенного вентиля обратной связи по всем выходам, кроме последнего, так что на входе присутствует 1, когда ни на одном этапе, кроме последнего, нет 1. [4]
Счетчик Джонсона, названный в честь Роберта Ройса Джонсона , представляет собой кольцо с инверсией; вот 4-битный счетчик Джонсона:
Обратите внимание на небольшой пузырек, указывающий на инверсию сигнала Q от последнего сдвигового регистра перед обратной подачей на первый вход D, что делает его счетчиком Джонсона.
История
До появления цифровых вычислений цифровые счетчики использовались для измерения скоростей случайных событий, таких как радиоактивные распады до альфа- и бета-частиц. Быстрые счетчики «предварительного масштабирования» снижали скорость случайных событий до более управляемых и более регулярных скоростей. Кольцевые счетчики с пятью состояниями использовались вместе с делящими на два масштабировщиками для создания декадных (степень десяти) масштабировщиков до 1940 года, таких как разработанные CE Wynn-Williams . [5]
Ранние кольцевые счетчики использовали только один активный элемент (вакуумную лампу, клапан или транзистор) на каскад, полагаясь на глобальную обратную связь, а не на локальные бистабильные триггеры, для подавления состояний, отличных от одногорячих состояний, например, в патентной заявке 1941 года Роберта Э. Маммы из National Cash Registor Company . [6] Уилкокс П. Овербек изобрел версию, использующую несколько анодов в одной вакуумной лампе, [7] [8] В знак признания его работы кольцевые счетчики иногда называют «кольцами Овербека» [9] [10] (а после 2006 года иногда «счетчиками Овербека», поскольку Википедия использовала этот термин с 2006 по 2018 год).
ENIAC использовал десятичную арифметику, основанную на 10-позиционных счетчиках с одним горячим кольцом. Работы Муммы из NCR и Овербека из MIT были среди работ предшествующего уровня техники, рассмотренных патентным бюро, в результате чего патенты Дж . Преспера Экерта и Джона Мочли на технологию ENIAC были признаны недействительными. [11]
К 1950-м годам появились кольцевые счетчики с двухламповым или двухтриодным триггером на каскад. [12]
Роберт Ройс Джонсон разработал ряд различных счетчиков на основе сдвигового регистра с целью создания различного количества состояний с максимально простой логикой обратной связи и подал заявку на патент в 1953 году. [13] Счетчик Джонсона является самым простым из них.
Приложения
Ранние применения кольцевых счетчиков были в качестве предделителей частоты (например, для счетчика Гейгера и подобных приборов), [5] в качестве счетчиков для подсчета появления шаблонов в криптоанализе (например, в машине для взлома кодов Хита Робинсона и компьютере Colossus ), [14] и в качестве элементов счетчика-аккумулятора для десятичной арифметики в компьютерах и калькуляторах, используя либо би-пятеричное (как в Colossus), либо десятизначное одночастичное (как в ENIAC ) представление.
Прямые кольцевые счетчики генерируют полностью декодированные коды one-hot, которые часто используются для включения определенного действия в каждом состоянии цикла циклического управления. Коды one-hot также могут быть декодированы из счетчика Джонсона, используя один вентиль для каждого состояния. [15] [nb 1]
Помимо того, что счетчик Джонсона является эффективным альтернативным способом генерации кодов one-hot и предварительных делителей частоты, он также является простым способом кодирования цикла четного числа состояний, которые могут быть асинхронно отобраны без сбоев, поскольку за раз изменяется только один бит, как в коде Грея . [16] Ранние компьютерные мыши использовали двунаправленные 2-битные кодировки Джонсона или Грея для обозначения движения в каждом из двух измерений, хотя у мышей эти коды обычно не генерировались кольцами триггеров (а вместо этого электромеханическими или оптическими квадратурными кодерами ). [17] 2-битный код Джонсона и 2-битный код Грея идентичны, в то время как для 3 или более бит коды Грея и Джонсона различны. В 5-битном случае код такой же, как код Либо-Крейга для десятичных цифр. [18] [19] [20] [21] [22] [23] [24] [25]
Счетчик шагающего кольца, также называемый счетчиком Джонсона, и несколько резисторов могут создать безглючное приближение синусоидальной волны. В сочетании с регулируемым предделителем это, возможно, самый простой генератор с числовым управлением . Два таких счетчика шагающего кольца, возможно, являются самым простым способом генерировать непрерывную фазовую частотную манипуляцию, используемую в двухтональной многочастотной сигнализации и ранних тонах модема . [26]
|
|
|
|
|
|
|
|
Смотрите также
Примечания
- ^ Схемы счетчика Джонсона с единичными состояниями, декодированными таким образом, можно найти в оригинальных конструкциях видеоадаптеров IBM MDA и CGA , в логике секвенсора синхронизации: одна или две 74x174 шестнадцатеричных D-триггерных микросхемы соединены как сдвиговый регистр, с обратной связью с инверсией для формирования счетчика Джонсона, а 2-входовые вентили NAND (в MDA) или вентили XOR (в CGA) используются для декодирования состояний, используемых в качестве сигналов, таких как +RAS (строб адреса строки [в DRAM ]) и S/-L (сдвиг / не загрузка). Источник: Технический справочник по опциям и адаптерам IBM для персональных компьютеров, логические схемы адаптера для монохромного дисплея и принтера; Технический справочник по опциям и адаптерам IBM для персональных компьютеров, логические схемы адаптера для цветного графического монитора.
Ссылки
- ^ Педрони, Вольней А. (2013). Конечные автоматы в оборудовании: теория и проектирование. MIT Press . стр. 50. ISBN 978-0-26201966-8.
- ^ Менджибар, Луис; Энтрена, Луис; Лоренц, Майкл Г.; Санчес-Рейльо, Рауль (2003). "Кодирование состояний для маломощных конечных автоматов в ПЛИС". Проектирование интегральных схем и систем. Моделирование, оптимизация и имитация мощности и синхронизации: Труды 13-го международного семинара, PATMOS 2003, Турин, Италия, 10–12 сентября 2003 г. Том 13. Springer Science & Business Media . стр. 35. ISBN 9783540200741.
- ^ Стэн, Мирча Р. (1997). "Синхронный счетчик вверх/вниз с периодом тактовой частоты, независимым от размера счетчика" (PDF) . Труды 13-го симпозиума IEEE по компьютерной арифметике : 274–281 .
- ^ Холдсворт, Брайан; Вудс, Клайв (2002). Цифровое логическое проектирование (4-е изд.). Newnes Books / Elsevier Science . стр. 191– 192. ISBN 0-7506-4588-2. Получено 19.04.2020 .
{{cite book}}: CS1 maint: проигнорированы ошибки ISBN ( ссылка )(519 страниц) [1] - ^ Льюис, Уилфрид Беннетт (1942). Электрический счет: со специальным указанием на подсчет альфа- и бета-частиц. Cambridge University Press . стр. 90. ISBN 9781316611760.
- ^ «Электронное накопление», патент США Роберта Э. Маммы № 2405096, поданный в 1941 году.
- ^ «Электронное коммутационное устройство», патент США № 2427533 Уилкокса П. Овербека, подан в 1943 году.
- ↑ Dayton Codebreakers: Исследовательский отчет 1942 года, упоминающий «Новый высокоскоростной счетчик г-на Овербека, 8 января 1942 года»
- ^ RAMAC 305 - IBM Customer Engineering Manual of Instruction (PDF) . IBM . 1959.
[…] Кольцо Overbeck используется для подачи синхронизированных импульсов в компьютерные схемы, подобно тому, как кулачковые выключатели подают синхронизированные импульсы в механические машины. Оно состоит из набора триггеров с общим входом от
линии привода кольца
, которая переносит импульсы, подаваемые технологическим барабаном. […] Первоначально триггеры сбрасываются в положение ВЫКЛ, за исключением исходного
триггера
, который включен. Каждый отрицательный входной импульс выключит триггер, который включен. Падение напряжения на выводе 10 триггера, который выключается, переключит сетку в положение ВКЛ. Это продолжается через замкнутое кольцо […]
- ^ Электротехника - Предлагаемая двухгодичная программа обучения после окончания средней школы. Серия программ технического образования. Соединенные Штаты, Отдел профессионального и технического образования. 1960. С. 52.
- ^ Рэндалл, Брайан (2014). «Истоки цифровых компьютеров: дополнительная библиография». В Metropolis, Николас (ред.). История вычислений в двадцатом веке . Elsevier. стр. 651– 652. ISBN 9781483296685.
- ^ Уильям Альфред Хигинботам , «Быстрые импульсные схемы», патент США № 2536808, поданный в 1949 году.
- ^ Роберт Ройс Джонсон , «Электронный счетчик», патент США № 3030581, подан в 1953 году.
- ^ Коупленд, Б. Джек (2010). Колосс: Секреты компьютеров Блетчли-Парка, взламывающих коды . Oxford University Press . С. 123–128 . ISBN 978-0-19957814-6.
- ^ Лангхольц, Гидеон; Кандел, Абрахам; Мотт, Джо Л. (1998). Основы проектирования цифровой логики. World Scientific. стр. 525–526 . ISBN 978-9-81023110-1.
- ^ van Holten, Cornelius (август 1982 г.). Написано в Делфтском техническом университете, Делфт, Нидерланды. «Цифровые делители с симметричными выходами — автор использует счетчики Джонсона с управляемой обратной связью для симметричных четных и нечетных делений тактового импульса» (PDF) . Wireless World . Том 88, № 1559. Саттон, Суррей, Великобритания: IPC Business Press Ltd. стр. 43–46 . ISSN 0043-6062. Архивировано (PDF) из оригинала 21.02.2021 . Получено 20.02.2021 .[2] [3] (4 страницы)
- ^ Lyon, Richard F. (август 1981 г.), Оптическая мышь и архитектурная методология для интеллектуальных цифровых датчиков (PDF) (отчет), Исследовательский центр Пало-Альто, Пало-Альто, Калифорния, США: Xerox Corporation , VLSI 81-1, архивировано (PDF) из оригинала 2020-05-23 , извлечено 2020-05-23 ,
Счетчики, необходимые для X и Y, просто считают через четыре состояния в любом направлении (вверх или вниз), изменяя только один бит за раз (т. е. 00, 01, 11, 10). Это простой случай счетчика кода Грея или счетчика Джонсона (счетчик Мебиуса).
(41 страница) - ^ Libaw, William H.; Craig, Leonard J. (октябрь 1953 г.) [сентябрь 1953 г.]. "Фотоэлектрический десятично-кодированный валовый дигитайзер". Труды профессиональной группы IRE по электронным компьютерам . EC-2 (3): 1– 4. doi :10.1109/IREPGELC.1953.5407731. eISSN 2168-1759. ISSN 2168-1740 . Получено 26.05.2020 .(4 страницы)
- ^ Powell, E. Alexander (июнь 1968 г.). «Коды, особенно полезные для аналого-цифровых преобразований». Краткая заметка о полезных кодах для схем управления потоками (PDF) . Крэнфилд, Великобритания: Колледж аэронавтики , кафедра производственного инжиниринга. стр. 10. S2CID 215864694. Памятка CoA 156. Архивировано (PDF) из оригинала 15.12.2020 . Получено 15.12.2020 .(18 страниц) (Примечание. В статье код Гликсона назван модифицированным кодом Грея , а имя Ричарда У. Хэмминга указано с ошибкой.)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (18 июня 1973 г.). Цифровая электроника. Техническая библиотека Philips (PTL) / Macmillan Education (переиздание 1-го изд. на английском языке). Эйндховен, Нидерланды: The Macmillan Press Ltd. / Gloeilampenfabrieken NV Philips . п. 43. дои : 10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. СБН 333-13360-9. Получено 2020-05-11 .(270 страниц)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1969]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik . Philips Fachbücher (на немецком языке). Том. Я (улучшенное и дополненное 5-е изд.). Гамбург, Германия: Deutsche Philips GmbH . стр. 52, 58, 98. ISBN. 3-87145-272-6.(xii+327+3 страницы)
- ^ Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1970]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Anwendung der digitalen Grundschaltungen und Gerätetechnik . Philips Fachbücher (на немецком языке). Том. II (4-е изд.). Гамбург, Германия: Deutsche Philips GmbH . п. 169. ИСБН 3-87145-273-4.(xi+393+3 страницы)
- ^ Штайнбух, Карл В. , изд. (1962). Написано в Карлсруэ, Германия. Taschenbuch der Nachrichtenverarbeitung (на немецком языке) (1-е изд.). Берлин / Геттинген / Нью-Йорк: Springer-Verlag OHG . стр. 71–72 , 74. LCCN 62-14511.
- ^ Штайнбух, Карл В .; Вагнер, Зигфрид В., ред. (1967) [1962]. Taschenbuch der Nachrichtenverarbeitung (на немецком языке) (2-е изд.). Берлин, Германия: Springer-Verlag OHG . LCCN 67-21079. Титул № 1036.
- ^ Штайнбух, Карл В .; Вебер, Вольфганг; Хайнеманн, Трауте, ред. (1974) [1967]. Taschenbuch der Informatik – Band II – Struktur und Programmierung von EDV-Systemen (на немецком языке). Том. 2 (3-е изд.). Берлин, Германия: Springer Verlag . ISBN 3-540-06241-6. LCCN 73-80607.
{{cite book}}:|work=проигнорировано ( помощь ) - ↑ Дон Ланкастер. «Кулинарная книга телевизионной пишущей машинки». ( TV Typewriter ). 1976. С. 180-181.