Изостазия
Изостазия (греч. ísos 'равный', stásis 'остановка') или изостатическое равновесие - это состояние гравитационного равновесия между земной корой (или литосферой ) и мантией , при котором кора "плавает" на высоте, которая зависит от ее толщины и плотности. Эта концепция привлекается для объяснения того, как на поверхности Земли могут существовать различные топографические высоты. Хотя первоначально она определялась в терминах континентальной коры и мантии [1] , впоследствии она была интерпретирована в терминах литосферы и астеносферы , особенно в отношении океанических островных вулканов [2] , таких как Гавайские острова .
Хотя Земля является динамической системой, которая реагирует на нагрузки многими различными способами, [3] изостазия описывает важный предельный случай, в котором кора и мантия находятся в статическом равновесии . Некоторые области (такие как Гималаи и другие конвергентные окраины) не находятся в изостатическом равновесии и не очень хорошо описываются изостатическими моделями.
Общий термин «изостазия» был введен в 1882 году американским геологом Кларенсом Даттоном . [4] [5] [6]
История концепции
В XVII и XVIII веках французские геодезисты (например, Жан Пикар ) пытались определить форму Земли ( геоид ), измеряя длину градуса широты на разных широтах ( измерение дуги ). Партия, работавшая в Эквадоре , знала, что ее отвесные линии , используемые для определения вертикального направления, будут отклоняться гравитационным притяжением близлежащих гор Анд . Однако отклонение было меньше ожидаемого, что было приписано горам с корнями малой плотности, которые компенсировали массу гор. Другими словами, корни гор малой плотности обеспечивали плавучесть, чтобы поддерживать вес гор над окружающей местностью. Аналогичные наблюдения в XIX веке британскими геодезистами в Индии показали, что это было широко распространенным явлением в горных районах. Позже было обнаружено, что разница между измеренным локальным гравитационным полем и тем, что ожидалось для высоты и локального рельефа ( аномалия Буге ), положительна над океаническими бассейнами и отрицательна над высокими континентальными областями. Это показывает, что низкая высота океанических бассейнов и высокая высота континентов также компенсируется на глубине. [7]
Американский геолог Кларенс Даттон использовал слово «изостазия» в 1889 году для описания этого общего явления. [4] [5] [6] Однако к тому времени уже были предложены две гипотезы, объясняющие это явление, в 1855 году: одна — Джорджем Эйри , а другая — Джоном Генри Праттом . [8] Гипотеза Эйри была позднее уточнена финским геодезистом Вейкко Алексантери Хейсканеном , а гипотеза Пратта — американским геодезистом Джоном Филмором Хейфордом . [3]
Гипотезы Эйри-Хейсканена и Пратта-Хейфорда предполагают, что изостазия отражает локальный гидростатический баланс. Третья гипотеза, литосферный изгиб , учитывает жесткость внешней оболочки Земли, литосферы . [9] Литосферный изгиб был впервые использован в конце 19 века для объяснения поднятых береговых линий в Скандинавии после таяния континентальных ледников в конце последнего оледенения . Он также использовался американским геологом Г. К. Гилбертом для объяснения поднятых береговых линий озера Бонневиль . [10] Эта концепция была дополнительно развита в 1950-х годах голландским геодезистом Венингом Мейнесом . [3]
Модели
Используются три основные модели изостазии: [3] [11]
- Модель Эйри-Хейсканена, в которой различные топографические высоты компенсируются изменениями толщины земной коры , при этом земная кора имеет постоянную плотность.
- Модель Пратта–Хейфорда, в которой различные топографические высоты компенсируются латеральными изменениями плотности горных пород .
- Модель Вененга-Мейнеса, или модель изгибной изостазии, в которой литосфера действует как упругая пластина, а ее присущая жесткость распределяет локальные топографические нагрузки по обширной области путем изгиба.
Изостазия Эйри и Пратта — это утверждения о плавучести, но изгибная изостазия — это утверждение о плавучести при прогибе листа с конечной упругой прочностью. Другими словами, модели Эйри и Пратта являются чисто гидростатическими, не учитывающими прочность материала, в то время как изгибная изостазия учитывает упругие силы от деформации жесткой коры. Эти упругие силы могут передавать выталкивающие силы через большую область деформации к более концентрированной нагрузке.
Идеальное изостатическое равновесие возможно только в том случае, если материал мантии находится в состоянии покоя. Однако в мантии присутствует тепловая конвекция . Это вводит вязкие силы, которые не учитываются в статической теории изостазии. Изостатическая аномалия или IA определяется как аномалия Буже за вычетом гравитационной аномалии из-за подповерхностной компенсации и является мерой локального отклонения от изостатического равновесия. В центре плато уровня она приблизительно равна аномалии свободного воздуха . [12] Такие модели, как глубокая динамическая изостазия (DDI), включают такие вязкие силы и применимы к динамической мантии и литосфере. [13] Измерения скорости изостатического отскока (возврата к изостатическому равновесию после изменения нагрузки коры) предоставляют информацию о вязкости верхней мантии. [14]
Воздушный
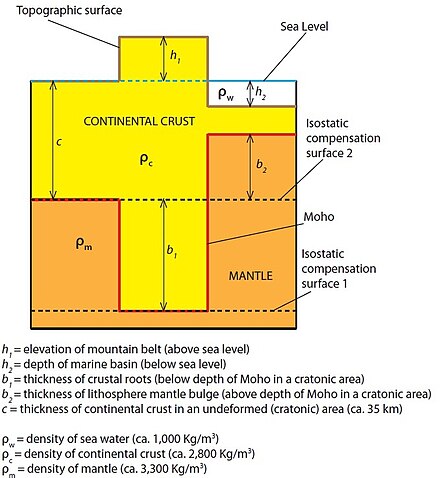
Основой модели является закон Паскаля и, в частности, его следствие, согласно которому в жидкости, находящейся в статическом равновесии, гидростатическое давление одинаково в каждой точке на одной и той же высоте (поверхность гидростатической компенсации): [3] [8]
h 1 ⋅ρ 1 = h 2 ⋅ρ 2 = h 3 ⋅ρ 3 = ... h n ⋅ρ n
Для представленного упрощенного рисунка глубина корней горного пояса (b 1 ) рассчитывается следующим образом:
где - плотность мантии (около 3300 кг м −3 ), а - плотность коры (около 2750 кг м −3 ). Таким образом, в общем случае:
- б 1 ≅ 5⋅ ч 1
В случае отрицательного рельефа (морской бассейн) балансировка литосферных колонн дает:
где - плотность мантии (около 3300 кг м −3 ), - плотность коры (около 2750 кг м −3 ) и - плотность воды (около 1000 кг м −3 ). Таким образом, в общем случае:
- б 2 ≅ 3,2⋅ ч 2
Пратт
Для показанной упрощенной модели новая плотность определяется по формуле: , где — высота горы, а c — толщина коры. [3] [15]
Vening Meinesz / изгиб

Эта гипотеза была предложена для объяснения того, как большие топографические нагрузки, такие как подводные горы (например, Гавайские острова ), могут быть компенсированы региональным, а не локальным смещением литосферы. Это более общее решение для литосферного изгиба , поскольку оно приближается к локально компенсированным моделям выше, поскольку нагрузка становится намного больше длины волны изгиба или жесткость изгиба литосферы приближается к нулю. [3] [9]
Например, вертикальное смещение z области океанической коры будет описываться дифференциальным уравнением
где и — плотности эстеносферы и океанской воды, g — ускорение силы тяжести, а — нагрузка на океаническую кору. Параметр D — изгибная жесткость , определяемая как
где E — модуль Юнга , — коэффициент Пуассона , — толщина литосферы. Решения этого уравнения имеют характерное волновое число
По мере того, как жесткий слой становится слабее, приближаясь к бесконечности, поведение приближается к чистому гидростатическому балансу гипотезы Эйри-Хейсканена. [14]
Глубина компенсации
Глубина компенсации (также известная как уровень компенсации , глубина компенсации или уровень компенсации ) — это глубина, ниже которой давление одинаково по всей горизонтальной поверхности. В стабильных регионах оно находится в глубокой коре, но в активных регионах оно может находиться ниже основания литосферы. [16] В модели Пратта это глубина, ниже которой все породы имеют одинаковую плотность; выше этой глубины плотность ниже там, где топографическая высота больше. [17]
Подразумеваемое
Осаждение и эрозия
Когда большие объемы осадков откладываются на определенном регионе, огромный вес новых осадков может привести к тому, что кора под ними опустится. Аналогично, когда большие объемы материала вымываются из региона, земля может подняться, чтобы компенсировать это. Поэтому, когда горный хребет вымывается, (уменьшенный) хребет отскакивает вверх (в определенной степени), чтобы быть размытым дальше. Некоторые из пластов горных пород, которые сейчас видны на поверхности земли, могли провести большую часть своей истории на больших глубинах под поверхностью, погребенные под другими пластами, чтобы в конечном итоге обнажиться, поскольку эти другие пласты вымывались, а нижние слои отскакивали вверх. [18]
Аналогию можно провести с айсбергом , который всегда плавает с определенной долей своей массы под поверхностью воды. Если снег выпадет на вершину айсберга, айсберг опустится ниже в воду. Если слой льда растает с вершины айсберга, оставшийся айсберг поднимется. Аналогично, литосфера Земли «плавает» в астеносфере. [8] [19]
Континентальные столкновения
Когда континенты сталкиваются, континентальная кора может утолщаться по краям при столкновении. Также очень часто одна из плит оказывается поджатой под другую плиту. В результате кора в зоне столкновения становится толщиной до 80 километров (50 миль) [20] по сравнению с 40 километрами (25 миль) для средней континентальной коры. [21] Как отмечалось выше, гипотеза Эйри предсказывает, что полученные корни гор будут примерно в пять раз глубже высоты гор, или 32 км против 8 км. Другими словами, большая часть утолщенной коры движется вниз , а не вверх, так же как большая часть айсберга находится под поверхностью воды.
Однако конвергентные границы плит тектонически очень активны, и их поверхностные особенности частично поддерживаются динамическими горизонтальными напряжениями, так что они не находятся в полном изостатическом равновесии. Эти регионы показывают самые высокие изостатические аномалии на поверхности Земли. [22]
Срединно-океанические хребты
Срединно-океанические хребты объясняются гипотезой Пратта как вышележащие области с необычно низкой плотностью в верхней мантии. [22] Это отражает тепловое расширение из-за более высоких температур, присутствующих под хребтами. [23]
Бассейн и хребет
В провинции Бассейна и Хребта на западе Северной Америки изостатическая аномалия невелика, за исключением побережья Тихого океана, что указывает на то, что регион в целом близок к изостатическому равновесию. Однако глубина до основания коры не сильно коррелирует с высотой рельефа. Это дает доказательства (через гипотезу Пратта), что верхняя мантия в этом регионе неоднородна, со значительными латеральными изменениями плотности. [22]
Ледяные щиты
Образование ледяных щитов может привести к опусканию поверхности Земли. Напротив, изостатический постледниковый отскок наблюдается в районах, когда-то покрытых ледяными щитами, которые теперь растаяли, например, вокруг Балтийского моря [24] и Гудзонова залива . [25] По мере отступления льда нагрузка на литосферу и астеносферу уменьшается, и они отскакивают обратно к своим равновесным уровням. Таким образом, можно найти бывшие морские скалы и связанные с ними волнорезные платформы в сотнях метров выше современного уровня моря . Движения отскока настолько медленные, что подъем, вызванный окончанием последнего ледникового периода , все еще продолжается. [18]
Помимо вертикального движения суши и моря, изостатическое регулирование Земли также включает горизонтальные движения. [26] Оно может вызвать изменения в гравитационном поле Земли [27] и скорости вращения , полярное смещение [ 28] и землетрясения [29] .
Граница литосферы и астеносферы
Гипотеза изостазии часто используется для определения положения границы литосферы и астеносферы (ЛАБ). [30]
Смотрите также
- Принцип Архимеда – Принцип плавучести в гидродинамике
- Уильям Боуи (инженер) – американский инженер-геодезист
- Лау, Готланд — округ острова Готланд, Швеция.
- Морская терраса – Возникающий прибрежный рельеф
- Гравитационная аномалия – разница между идеальным и наблюдаемым ускорением свободного падения в определенном месте.
- Гравитационная карта
- Хронология развития тектонофизики (до 1954 г.)
Ссылки
- ^ 33. Спасоевич, С. и Гурнис, М., 2012, Уровень моря и вертикальное движение континентов по динамическим моделям Земли с позднего мелового периода: Бюллетень Американской ассоциации геологов-нефтяников, т. 96, № 11, стр. 2037–2064.
- ^ 13. Foulger, GR, Pritchard, MJ, Julian, BR, Evans, JR, Allen, RM, Nolet, G., Morgan, WJ, Bergsson, BH, Erlendsson, P., Jakobsdottir, S., Ragnarsson, S., Stefansson, R., Vogfjord, K., 2000. Сейсмическая аномалия под Исландией простирается до переходной зоны мантии и не глубже. Geophys. J. Int. 142, F1–F5.
- ^ abcdefg Уоттс, AB (2001). Изостазия и изгиб литосферы . Cambridge University Press. ISBN 0521622727.
- ^ ab Даттон, Кларенс (1882). «Физика земной коры; обсуждение». American Journal of Science . 3. 23 (апрель): 283–290. Bibcode : 1882AmJS...23..283D. doi : 10.2475/ajs.s3-23.136.283. S2CID 128904689.
- ^ ab Orme, Anthony (2007). «Кларенс Эдвард Даттон (1841–1912): солдат, эрудит и эстет». Геологическое общество, Лондон, Специальные публикации . 287 (1): 271–286. Bibcode : 2007GSLSP.287..271O. doi : 10.1144/SP287.21. S2CID 128576633.
- ^ ab Longwell, Chester R. (1958). "Кларенс Эдвард Даттон" (PDF) . Вашингтон, округ Колумбия: Национальная академия наук . Получено 24 марта 2022 г. .
- ^ Кири, П.; Клепейс, Калифорния; Вайн, Ф.Дж. (2009). Глобальная тектоника (3-е изд.). Оксфорд: Уайли-Блэквелл. п. 42. ИСБН 9781405107778.
- ^ abc Кирей, Клепеис и Вайн 2009, стр. 43.
- ^ аб Кири, Klepeis & Vine 2009, стр. 44–45.
- ^ Гилбер, Г. К. (1890). «Озеро Бонневиль». Монография Геологической службы США . 1. doi :10.3133/m1 .
- ^ Кири, Клепеис и Вайн 2009, стр. 42–45.
- ^ Кири, Клепеис и Вайн 2009, стр. 45–48.
- ^ Чеховский, Л. (2019). «Мантийный поток и определение положения LAB при условии изостазии». Чистая и прикладная геофизика . 176 (6): 2451–2463. Bibcode : 2019PApGe.176.2451C. doi : 10.1007/s00024-019-02093-8 .
- ^ ab Kearey, Klepeis & Vine 2009, стр. 45.
- ^ Кири, Клепеис и Вайн 2009, стр. 43–44.
- ^ Джексон, Джулия А., ред. (1997). "глубина компенсации". Глоссарий геологии (четвертое изд.). Александрия, Вирджиния: Американский геологический институт. ISBN 0922152349.
- ^ Аллаби, Майкл (2013). «Модель Пратта». Словарь геологии и наук о Земле (Четвертое издание). Оксфорд: Oxford University Press. ISBN 9780199653065.
- ^ аб Кири, Klepeis & Vine 2009, стр. 45–46.
- ^ Монро, Джеймс С. (1992). Физическая геология: исследование Земли . Сент-Пол: West Pub. Co. стр. 305. ISBN 0314921958.
- ^ Кири, Клепеис и Вайн 2009, стр. 322.
- ^ Кири, Клепеис и Вайн 2009, стр. 19.
- ^ abc Кирей, Клепеис и Вайн 2009, стр. 48.
- ^ Филпоттс, Энтони Р.; Агу, Джей Дж. (2009). Принципы магматической и метаморфической петрологии (2-е изд.). Кембридж, Великобритания: Cambridge University Press. С. 6–10. ISBN 9780521880060.
- ^ Эронен, Матти; Глюкерт, Гуннар; Хатакка, Ласси; Ван де Пласше, Орсон; Ван дер Плихт, Йоханнес; Рантала, Паси (28 июня 2008 г.). «Скорости голоценового изостатического поднятия и относительного понижения уровня моря Балтийского моря на юго-западе Финляндии на основе исследований изоляционных контактов». Борей . 30 (1): 17–30. doi :10.1111/j.1502-3885.2001.tb00985.x. S2CID 54582233 . Проверено 15 ноября 2022 г.
- ^ Балестра, Барбара; Бертини, Адель; Де Верналь, Энн; Монеки, Симонетта; Реале, Вивиана (1 октября 2013 г.). «Позднечетвертичные условия морской поверхности в Лаврентийском конусе выноса: данные по кокколитам и диноцистам». Палеогеография, Палеоклиматология, Палеоэкология . 387 : 200–210. Bibcode :2013PPP...387..200B. doi :10.1016/j.palaeo.2013.07.002 . Получено 15 ноября 2022 г.
- ^ Джеймс, Томас С.; Морган, У. Джейсон (июнь 1990 г.). «Горизонтальные движения, вызванные послеледниковым отскоком». Geophysical Research Letters . 17 (7): 957–960. Bibcode : 1990GeoRL..17..957J. doi : 10.1029/GL017i007p00957.
- ^ Alexander, JC (ноябрь 1983 г.). «Высшие гармонические эффекты гравитационного поля Земли от послеледникового отскока, наблюдаемые Лагеосом». Geophysical Research Letters . 10 (11): 1085–1087. Bibcode : 1983GeoRL..10.1085A. doi : 10.1029/GL010i011p01085.
- ^ Wahr, John ; Dazhong, Han; Trupin, Andrew; Lindqvist, Varna (ноябрь 1993 г.). «Вековые изменения вращения и гравитации: свидетельство постледникового отскока или изменений в полярном льду?». Advances in Space Research . 13 (11): 257–269. Bibcode : 1993AdSpR..13k.257W. doi : 10.1016/0273-1177(93)90228-4.
- ^ Дэвенпорт, Колин А.; Рингроуз, Филип С.; Беккер, Амфрид; Хэнкок, Пол; Фентон, Кларк (1989). «Геологические исследования поздне- и постледниковой сейсмической активности в Шотландии». Землетрясения на североатлантических пассивных окраинах: неотектоника и постледниковый отскок . стр. 175–194. doi :10.1007/978-94-009-2311-9_11. ISBN 978-94-010-7538-1.
- ^ Гринч, М.; Зейен, Х.; Белик, М. (2014). «Автоматическое 1D интегрированное геофизическое моделирование литосферных разрывов: исследование случая Карпато-Паннонского бассейна». Вклад в Geophysics and Geodesy . 44 (2): 115–131. Bibcode : 2014CoGG...44..115G. doi : 10.2478/congeo-2014-0007 . S2CID 129497623. Получено 13 декабря 2021 г.
Дальнейшее чтение
- Лисицын, Эжени (1974). Изменения уровня моря. Амстердам: Elsevier Scientific Pub. Co. ISBN 9780080870441. Получено 23 марта 2022 г. .
Внешние ссылки
- Олдхэм, Ричард Диксон (1922). . Encyclopaedia Britannica (12-е изд.).





![{\displaystyle c\rho _{c}=(h_{2}\rho _{w})+(b_{2}\rho _{m})+[(c-h_{2}-b_{2})\rho _{c}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fed9708a37e32b3c6e88d7353e28bb979f8de9f)










![{\displaystyle \kappa = {\sqrt[{4}]{(\rho _{m}-\rho _{w})g/4D}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26610c59d48b3e4b5e0bcf2320f97228557e62b6)
