Неправильная луна
В астрономии нерегулярная луна , нерегулярный спутник или нерегулярный естественный спутник — это естественный спутник, следующий по далекой, наклонной и часто сильно эллиптической и ретроградной орбите . Они были захвачены своей родительской планетой, в отличие от регулярных спутников , которые образовались на орбите вокруг них. Нерегулярные луны имеют стабильную орбиту, в отличие от временных спутников , которые часто имеют такие же нерегулярные орбиты, но в конечном итоге уйдут. Термин не относится к форме; Тритон , например, является круглой луной, но считается неправильной из-за своей орбиты и происхождения.
По состоянию на февраль 2024 года [обновлять]известно о 228 нерегулярных спутниках, вращающихся вокруг всех четырех внешних планет ( Юпитера , Сатурна , Урана и Нептуна ). Крупнейшими из каждой планеты являются Гималия Юпитера, Феба Сатурна, Сикоракс Урана и Тритон Нептуна. Тритон довольно необычен для нерегулярного спутника; если его исключить, то Нереида является крупнейшим нерегулярным спутником Нептуна. В настоящее время считается, что нерегулярные спутники когда-то были независимыми объектами, вращающимися вокруг Солнца, прежде чем были захвачены близлежащей планетой в начале истории Солнечной системы. Альтернатива предполагает, что они возникли дальше в поясе Койпера [1] и были захвачены после близкого пролета другой звезды [2].
Определение
| Планета | Радиус холма r H ( 10 6 км ) [3] | г Н ( ° ) [3] | Число известно | Самый дальний известный спутник (10 6 км) |
|---|---|---|---|---|
| Юпитер | 51 | 4.7 | 87 | 24,2 (0,47r H ) |
| Сатурн | 69 | 3.0 | 122 | 26,4 (0,38r H ) |
| Уран | 73 | 1.5 | 10 | 20,4 (0,28r H ) |
| Нептун | 116 | 1.5 | 9 (включая Тритон) | 50,6 (0,44r H ) |
Не существует общепринятого точного определения нерегулярного спутника. Неформально спутники считаются нерегулярными, если они находятся достаточно далеко от планеты, что прецессия их орбитальной плоскости в первую очередь контролируется Солнцем, другими планетами или другими лунами. [4]
На практике большая полуось спутника сравнивается с радиусом сферы Хилла планеты (то есть сферы ее гравитационного влияния), . Неправильные спутники имеют большие полуоси больше 0,05 с апоапсидами, простирающимися до 0,65 . [3] Радиус сферы Хилла указан в соседней таблице: Уран и Нептун имеют большие радиусы сферы Хилла, чем Юпитер и Сатурн, несмотря на то, что они менее массивны, поскольку они находятся дальше от Солнца. Однако ни один известный неправильный спутник не имеет большую полуось, превышающую 0,47 . [5]
Луна Земли, по-видимому, является исключением: она обычно не указывается как нерегулярный спутник, хотя ее прецессия в основном контролируется Солнцем [ требуется ссылка ] , а ее большая полуось больше 0,05 радиуса сферы Хилла Земли. С другой стороны, Тритон Нептуна , который, вероятно, является захваченным объектом, обычно указывается как нерегулярный, несмотря на то, что находится в пределах 0,05 радиуса сферы Хилла Нептуна, так что прецессия Тритона в основном контролируется сжатием Нептуна, а не Солнцем. [5] Нептунова Нереида и Сатурнианский Япет имеют большие полуоси, близкие к 0,05 радиуса сфер Хилла их родительских планет: Нереида (с очень эксцентричной орбитой) обычно указывается как нерегулярный, но не Япет.
Орбиты
Текущее распределение

Орбиты известных нерегулярных спутников чрезвычайно разнообразны, но существуют определенные закономерности. Ретроградные орбиты встречаются гораздо чаще (83%), чем прямые. Неизвестны спутники с наклоном орбиты выше 60° (или ниже 130° для ретроградных спутников); более того, за исключением Нереиды, ни одна нерегулярная луна не имеет наклона менее 26°, а наклоны выше 170° встречаются только в системе Сатурна. Кроме того, можно выделить некоторые группировки, в которых один большой спутник делит похожую орбиту с несколькими меньшими. [5]
Учитывая их удаленность от планеты, орбиты внешних спутников сильно возмущены Солнцем, и их орбитальные элементы сильно меняются за короткие промежутки времени. Например, большая полуось Пасифаи изменяется на 1,5 Гм за два года (одна орбита), наклон около 10°, а эксцентриситет на 0,4 за 24 года (два периода обращения Юпитера). [6] Следовательно, для идентификации группировок используются средние орбитальные элементы (усредненные по времени), а не оскулирующие элементы на заданную дату. (Аналогично, для определения семейств астероидов используются собственные орбитальные элементы .)
Источник
Неправильные спутники могли быть захвачены с гелиоцентрических орбит. (Действительно, похоже, что неправильные луны гигантских планет, троянцы Юпитера и Нептуна , а также объекты серого пояса Койпера имеют схожее происхождение. [7] ). В качестве альтернативы, транснептуновые объекты могли быть занесены из-за близко проходящей звезды , и часть этих занесенных транснептуновых объектов была захвачена гигантскими планетами. [8] Для того чтобы это произошло, должно произойти по крайней мере одно из трех:
- рассеивание энергии (например, при взаимодействии с первичным газовым облаком)
- существенное (40%) расширение сферы Хилла планеты за короткий период времени (тысячи лет)
- передача энергии при взаимодействии трех тел . Это может включать:
- столкновение (или близкое сближение) приближающегося тела и спутника, в результате которого приближающееся тело теряет энергию и захватывается.
- близкое столкновение между входящим двойным объектом и планетой (или, возможно, существующей луной), в результате чего один компонент двойника был захвачен. Такой маршрут был предложен как наиболее вероятный для Тритона . [9]
После захвата некоторые спутники могут распасться, что приведет к группировкам более мелких лун, следующих по схожим орбитам. Резонансы могут еще больше изменить орбиты, сделав эти группировки менее узнаваемыми.
Долгосрочная стабильность
Текущие орбиты нерегулярных лун стабильны, несмотря на существенные возмущения вблизи апоцентра . [10] Причиной этой стабильности у ряда нерегулярных лун является тот факт, что они вращаются по орбитам с вековым или резонансом Козаи . [11]
Кроме того, моделирование позволяет сделать следующие выводы:
- Орбиты с наклоном от 50° до 130° очень нестабильны: их эксцентриситет быстро увеличивается, что приводит к потере спутника [6]
- Ретроградные орбиты более стабильны, чем прямые (стабильные ретроградные орбиты можно найти дальше от планеты)
Увеличение эксцентриситета приводит к уменьшению перицентров и увеличению апоцентров. Спутники попадают в зону обычных (больших) лун и теряются или выбрасываются из-за столкновений и близких сближений. В качестве альтернативы, увеличивающиеся возмущения Солнца в растущих апоцентрах выталкивают их за пределы сферы Хилла.
Ретроградные спутники можно обнаружить дальше от планеты, чем прямые. Подробные численные интегрирования показали эту асимметрию. Пределы являются сложной функцией наклона и эксцентриситета, но в целом прямые орбиты с большой полуосью до 0,47 r H (радиус сферы Хилла) могут быть устойчивыми, тогда как для ретроградных орбит устойчивость может распространяться до 0,67 r H .
Граница для большой полуоси на удивление резкая для прямых спутников. Спутник на прямой круговой орбите (наклонение = 0°), размещенный на 0,5 r H, покинет Юпитер всего за сорок лет. Эффект можно объяснить так называемым резонансом эвекции . Апоцентр спутника, где сцепление планеты с луной наиболее слабое, попадает в резонанс с положением Солнца. Эффекты возмущения накапливаются при каждом проходе, выталкивая спутник еще дальше наружу. [10]
Асимметрию между прямыми и ретроградными спутниками можно объяснить очень интуитивно ускорением Кориолиса в системе отсчета, вращающейся вместе с планетой. Для прямых спутников ускорение направлено наружу, а для ретроградных — внутрь, стабилизируя спутник. [12]
Временные захваты
Захват астероида с гелиоцентрической орбиты не всегда является постоянным. Согласно моделированию, временные спутники должны быть обычным явлением. [13] [14] Единственными наблюдаемыми примерами являются 2006 RH 120 и 2020 CD 3 , которые были временными спутниками Земли, открытыми в 2006 и 2020 годах соответственно. [15] [16] [17]
Физические характеристики
Графики недоступны из-за технических проблем. Более подробная информация на Phabricator и на MediaWiki.org. |
Размер

Поскольку объекты определенного размера тем труднее увидеть, чем больше их расстояние от Земли, известные нерегулярные спутники Урана и Нептуна больше, чем у Юпитера и Сатурна; более мелкие, вероятно, существуют, но пока не наблюдались. Принимая во внимание эту предвзятость наблюдений, распределение размеров нерегулярных спутников, по-видимому, похоже на все четыре гигантские планеты.
Распределение размеров астероидов и многих подобных популяций можно выразить в виде степенного закона : мелких объектов гораздо больше, чем крупных, и чем меньше размер, тем объект многочисленнее. Математическое соотношение, выражающее количество объектов, , с диаметром, меньшим определенного размера, , аппроксимируется как:
- где q определяет наклон.
Значение q определяется путем наблюдения.
Для нерегулярных лун наблюдается пологий степенной закон ( q ≃ 2) для размеров от 10 до 100 км, † но более крутой закон ( q ≃ 3,5) наблюдается для объектов размером менее 10 км. Анализ изображений, полученных телескопом Канада-Франция-Гавайи в 2010 году, показывает, что степенной закон для популяции малых ретроградных спутников Юпитера, вплоть до предела обнаружения ≈ 400 м, является относительно пологим, при q ≃ 2,5. Таким образом, можно экстраполировать, что Юпитер должен иметь600+600
−300Луны диаметром 400 м и более. [18]
Для сравнения, распределение крупных объектов пояса Койпера гораздо круче ( q ≈ 4). То есть, на каждый объект диаметром 1000 км приходится тысяча объектов диаметром 100 км, хотя неизвестно, насколько далеко простирается это распределение. Распределение размеров популяции может дать представление о ее происхождении, будь то захват, столкновение и распад или аккреция.
† На каждый объект размером 100 км можно найти десять объектов размером 10 км.
Вокруг каждой гигантской планеты есть один нерегулярный спутник, который доминирует, имея более трех четвертей массы всей нерегулярной спутниковой системы: Гималия Юпитера (около 75%), Феба Сатурна (около 98%), Сикоракс Урана (около 90%) и Нептуна Нереида (около 98%). Нереида также доминирует среди нерегулярных спутников, взятых вместе, имея около двух третей массы всех нерегулярных лун вместе взятых. Феба составляет около 17%, Сикоракс около 7% и Гималия около 5%: остальные луны в сумме составляют около 4%. (В этом обсуждении Тритон не включен.) [5]
Цвета

Цвета нерегулярных спутников можно изучать с помощью индексов цвета : простых мер различий видимой величины объекта через синий (B), видимый , т.е. зелено-желтый (V), и красный (R) фильтры . Наблюдаемые цвета нерегулярных спутников варьируются от нейтральных (сероватых) до красноватых (но не таких красных, как цвета некоторых объектов пояса Койпера).
| альбедо [19] | нейтральный | красноватый | красный |
|---|---|---|---|
| низкий | С 3–8% | П 2–6% | Д 2–5% |
| середина | М 10–18% | А 13–35% | |
| высокий | Э 25–60% |
Каждая система планет демонстрирует немного отличающиеся характеристики. Нерегулярные объекты Юпитера имеют серый или слегка красный цвет, что соответствует астероидам C , P и D-типа . [20] Некоторые группы спутников, как наблюдалось, демонстрируют похожие цвета (см. последующие разделы). Нерегулярные объекты Сатурна немного краснее, чем у Юпитера.
Крупные нерегулярные спутники Урана ( Сикоракс и Калибан ) светло-красные, тогда как меньшие Просперо и Сетебос серые, как и спутники Нептуна Нереида и Галимеда . [21]
Спектры
При текущем разрешении видимые и ближние инфракрасные спектры большинства спутников кажутся невыразительными. До сих пор водяной лед был выведен на Фебе и Нереиде, а особенности, приписываемые водным изменениям, были обнаружены на Гималии. [ необходима цитата ]
Вращение
Регулярные спутники обычно приливно заблокированы (то есть их орбита синхронна с их вращением, так что они показывают только одну сторону к своей родительской планете). Напротив, приливные силы на нерегулярных спутниках пренебрежимо малы, учитывая их расстояние от планеты, и периоды вращения в диапазоне всего десяти часов были измерены для самых больших лун Гималии , Фебы , Сикоракса и Нереиды (для сравнения с их орбитальными периодами в сотни дней). Такие скорости вращения находятся в том же диапазоне, что и типичные для астероидов . [ требуется цитата ] Тритон, будучи намного больше и ближе к своей родительской планете, приливно заблокирован.
Семьи с общим происхождением
Некоторые нерегулярные спутники, по-видимому, вращаются в «группах», в которых несколько спутников имеют схожие орбиты. Ведущая теория заключается в том, что эти объекты представляют собой столкновительные семьи , части более крупного тела, которое распалось.
Динамические группировки
Простые модели столкновений могут быть использованы для оценки возможного рассеивания орбитальных параметров при заданном импульсе скорости Δ v . Применение этих моделей к известным орбитальным параметрам позволяет оценить Δ v, необходимое для создания наблюдаемого рассеивания. Δ v в десятки метров в секунду (5–50 м/с) может быть результатом распада. Динамические группировки нерегулярных спутников могут быть идентифицированы с использованием этих критериев, а также оценена вероятность общего происхождения от распада. [22]
Когда дисперсия орбит слишком велика (т.е. потребуется Δ v порядка сотен м/с)
- либо следует предположить более одного столкновения, т.е. кластер следует дополнительно подразделить на группы
- или необходимо постулировать существенные изменения после столкновения, например, в результате резонансов.
Цветовые группы
Когда цвета и спектры спутников известны, однородность этих данных для всех членов данной группы является существенным аргументом в пользу общего происхождения. Однако отсутствие точности в имеющихся данных часто затрудняет получение статистически значимых выводов. Кроме того, наблюдаемые цвета не обязательно отражают основной состав спутника.
Наблюдаемые группировки
Неправильные спутники Юпитера

Обычно перечисляются следующие группы (динамически плотные группы, отображающие однородные цвета, выделены жирным шрифтом ):
- Спутники Prograde
- Группа Гималии имеет средний наклон 28°. Они ограничены динамически (Δ v ≈ 150 м/с). Они однородны в видимых длинах волн (имея нейтральные цвета, похожие на цвета астероидов C-типа ) и в ближнем инфракрасном диапазоне [23]
- Прямоугольные спутники Themisto , Carpo и Valetudo не входят ни в одну известную группу.

Юпитер · Гималии · Каллисто
- Ретроградные спутники
- Группа Карме имеет средний наклон 165°. Она динамически плотная (5 < Δ v < 50 м/с). Она очень однородна по цвету, каждый член имеет светло-красную окраску, соответствующую астероиду-прародителю D-типа .
- Группа Ананке имеет средний наклон 148°. Она показывает небольшой разброс орбитальных параметров (15 < Δ v < 80 м/с). Сама Ананке выглядит светло-красной, но другие члены группы серые.
- Группа Pasiphae очень рассеяна. Сама Pasiphae выглядит серой, тогда как другие ее члены ( Callirrhoe , Megaclite ) светло-красные.
Синопа , иногда включаемая в группу Пасифа, красная и, учитывая разницу в наклоне, ее можно было бы запечатлеть независимо. [20] [24] Пасифа и Синопа также находятся в вековых резонансах с Юпитером. [10] [22]
Неправильные спутники Сатурна

Обычно спутники Сатурна классифицируют по следующим группам:
- Спутники Prograde
- Группа Галлии имеет средний наклон 34°. Их орбиты динамически плотные (Δ v ≈ 50 м/с), и они светло-красного цвета; окраска однородна как в видимом, так и в ближнем инфракрасном диапазоне длин волн. [23]
- Группа инуитов имеет средний наклон 46°. Их орбиты широко разбросаны (Δ v ≈ 350 м/с), но они физически однородны, разделяя светло-красную окраску.
- Ретроградные спутники
- Группа Норсе определяется в основном для целей наименования; орбитальные параметры очень широко разбросаны. Были исследованы подгруппы, включая
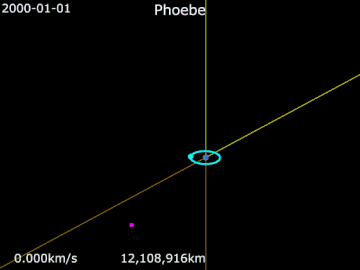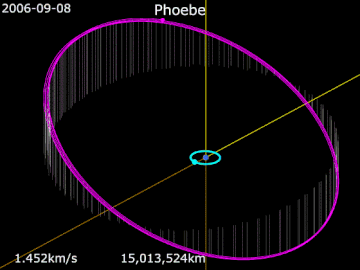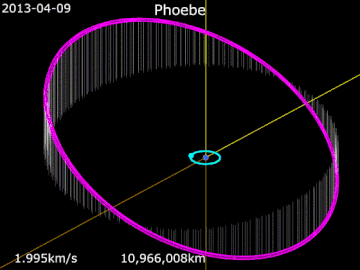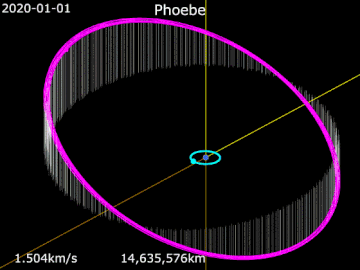
- Анимация орбиты Фиби.
Сатурн · Фиби · Титан
Неправильные спутники Урана и Нептуна

| Планета | г мин [3] |
|---|---|
| Юпитер | 1,5 км |
| Сатурн | 3 км |
| Уран | 7 км |
| Нептун | 16 км |
Согласно современным знаниям, число нерегулярных спутников, вращающихся вокруг Урана и Нептуна, меньше, чем у Юпитера и Сатурна. Однако считается, что это просто результат трудностей наблюдения из-за большего расстояния до Урана и Нептуна. Таблица справа показывает минимальный радиус (r min ) спутников, которые можно обнаружить с помощью современных технологий, предполагая альбедо 0,04; таким образом, почти наверняка существуют небольшие луны Урана и Нептуна, которые пока не видны.
Из-за меньшего числа статистически значимые выводы о группировках затруднительны. Единое происхождение ретроградных нерегулярных объектов Урана кажется маловероятным, учитывая дисперсию орбитальных параметров, которая потребовала бы высокого импульса (Δ v ≈ 300 км), что подразумевает большой диаметр ударника (395 км), что, в свою очередь, несовместимо с распределением размеров фрагментов. Вместо этого было высказано предположение о существовании двух группировок: [20]
Эти две группы различаются (с уверенностью 3σ) по своему расстоянию от Урана и по своему эксцентриситету. [25] Однако эти группировки напрямую не подтверждаются наблюдаемыми цветами: Калибан и Сикоракс кажутся светло-красными, тогда как меньшие луны — серыми. [21]
Для Нептуна было отмечено возможное общее происхождение Псаматы и Несо . [26] Учитывая схожие (серые) цвета, было также высказано предположение, что Галимеда может быть фрагментом Нереиды. [21] У этих двух спутников была очень высокая вероятность (41%) столкновения за время существования Солнечной системы. [27]
Исследование

На сегодняшний день единственными нерегулярными спутниками, которые удалось посетить с близкого расстояния с помощью космического аппарата, являются Тритон и Феба , крупнейшие из нерегулярных спутников Нептуна и Сатурна соответственно. Тритон был получен «Вояджером-2» в 1989 году, а «Феба» — зондом «Кассини» в 2004 году. « Вояджер -2» также сделал отдалённое изображение Нереиды Нептуна в 1989 году, а «Кассини» сделал отдалённое изображение Гималии Юпитера в низком разрешении в 2000 году. многие сатурнианские иррегулярные явления наблюдались издалека: Альбиорикс , Бебхионн , Бергельмир , Бестла , Эрриапус , Форньот , Грейп , Хати , Хюрроккин , Иджирак , Кари , Кивиук , Логе , Мундильфари , Нарви , Паалиак , Сиарнак , Скати , Сколл , Суттунгр . , Таркек , Тарвос , Тримр и Имир . [5]
Планируется, что миссия « Тяньвэнь -4» (запуск в 2029 году) будет сосредоточена на регулярной луне Каллисто вокруг Юпитера, но она может пролететь мимо нескольких нерегулярных спутников Юпитера, прежде чем выйти на орбиту Каллистона. [28]
Галерея
- 71 неправильный спутник Юпитера (с Каллисто для сравнения; другие галилеевские спутники также видны около центра, хотя и не обозначены явно). Данные по состоянию на 2021 год.
- 122 нерегулярных спутника Сатурна (с Титаном, Гиперионом и Япетом для сравнения). Данные по состоянию на 2023 год.
- 9 нерегулярных спутников Урана. Данные на 2021 год.
- 6 нерегулярных лун Нептуна (без Тритона). Данные на 2021 год.
Ссылки
- ^ Пфальцнер, Сюзанна; Говинд, Амит; Вагнер, Фрэнк В. (2024-09-01). «Нерегулярные луны, возможно, выброшенные из внешней Солнечной системы при пролете звезды». The Astrophysical Journal Letters . 972 (2): L21. arXiv : 2409.03529 . Bibcode : 2024ApJ...972L..21P. doi : 10.3847/2041-8213/ad63a6 . ISSN 2041-8205.
- ^ Пфальцнер, Сюзанна; Говинд, Амит; Портегис Цварт, Саймон (2024-09-04). «Траектория пролета звезды, сформировавшего внешнюю часть Солнечной системы». Nature Astronomy : 1–7. arXiv : 2409.03342 . Bibcode :2024NatAs.tmp..242P. doi :10.1038/s41550-024-02349-x. ISSN 2397-3366.
{{cite journal}}: CS1 maint: bibcode ( ссылка ) - ^ abcd Шеппард, СС (2006). «Внешние нерегулярные спутники планет и их связь с астероидами, кометами и объектами пояса Койпера». Труды Международного астрономического союза . 1 : 319–334. arXiv : astro-ph/0605041 . Bibcode : 2006IAUS..229..319S. doi : 10.1017/S1743921305006824. S2CID 2077114.
- ^ "Planetary Satellite Mean Orbital Parameters". Jet Propulsion Laboratory . Архивировано из оригинала 6 октября 2021 г. Получено 15 января 2024 г.
- ^ abcde Denk, Tilmann (2024). "Внешние луны Сатурна". tilmanndenk.de . Tilmann Denk. Архивировано из оригинала 24 февраля 2024 года . Получено 25 февраля 2024 года .
- ^ ab Carruba, V.; Burns, Joseph A.; Nicholson, Philip D.; Gladman, Brett J. (2002). "On the Inclination Distribution of the Jovian Irregular Satellites" (PDF) . Icarus . 158 (2): 434–449. Bibcode :2002Icar..158..434C. doi :10.1006/icar.2002.6896. Архивировано (PDF) из оригинала 27.02.2009 . Получено 09.09.2006 .
- ^ Шеппард, СС; Трухильо, Калифорния (2006). «Густое облако троянцев Нептуна и их цвета». Science . 313 (5786): 511–514. Bibcode :2006Sci...313..511S. doi :10.1126/science.1127173. PMID 16778021. S2CID 35721399.
- ^ Пфальцнер, Сюзанна; Говинд, Амит; Вагнер, Фрэнк В. (сентябрь 2024 г.). «Нерегулярные луны, возможно, выброшенные из внешней Солнечной системы при пролете звезды». The Astrophysical Journal Letters . 972 (2): L21. arXiv : 2409.03529 . Bibcode : 2024ApJ...972L..21P. doi : 10.3847/2041-8213/ad63a6 . ISSN 2041-8205.
- ^ Агнор, К. Б. и Гамильтон, Д. П. (2006). «Захват Нептуном своей луны Тритона в гравитационном столкновении с двойной планетой». Nature . 441 (7090): 192–4. Bibcode :2006Natur.441..192A. doi :10.1038/nature04792. PMID 16688170. S2CID 4420518.
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ abc Nesvorný, David; Alvarellos, Jose LA; Dones, Luke; Levison, Harold F. (2003). "Orbital and Collisional Evolution of the Irregular Satellites" (PDF) . The Astronomical Journal . 126 (1): 398. Bibcode :2003AJ....126..398N. doi :10.1086/375461. S2CID 8502734. Архивировано из оригинала (PDF) 2020-04-15 . Получено 2006-07-29 .
- ^ Ćuk, Matija; Burns, Joseph A. (2004). «О вековом поведении нерегулярных спутников». The Astronomical Journal . 128 (5): 2518–2541. arXiv : astro-ph/0408119 . Bibcode : 2004AJ....128.2518C. doi : 10.1086/424937. S2CID 18564122.
- ^ Гамильтон, Дуглас П.; Бернс, Джозеф А. (1991). «Зоны орбитальной устойчивости вокруг астероидов». Icarus . 92 (1): 118–131. Bibcode :1991Icar...92..118H. doi : 10.1016/0019-1035(91)90039-V .
- ↑ Камилла М. Карлайл (30 декабря 2011 г.). «Псевдолуны вращаются вокруг Земли». Sky & Telescope .
- ^ Федорец, Григорий; Гранвик, Микаэль; Джедик, Роберт (15 марта 2017 г.). «Распределение орбит и размеров астероидов, временно захваченных системой Земля-Луна». Icarus . 285 : 83–94. Bibcode :2017Icar..285...83F. doi :10.1016/j.icarus.2016.12.022.
- ^ "2006 RH120 ( = 6R10DB9) (Вторая луна для Земли?)". Обсерватория Грейт-Шеффорд. 14 сентября 2017 г. Архивировано из оригинала 2015-02-06 . Получено 2017-11-13 .
- ↑ Roger W. Sinnott (17 апреля 2007 г.). "Earth's "Other Moon"". Sky & Telescope . Архивировано из оригинала 2012-04-02 . Получено 2017-11-13 .
- ^ "MPEC 2020-D104 : 2020 CD3: Временно захваченный объект". Minor Planet Electronic Circular . Minor Planet Center . 25 февраля 2020 г. Архивировано из оригинала 22 октября 2020 г. Получено 25 февраля 2020 г.
- ^ Эштон, Эдвард; Бодуан, Мэтью; Глэдман, Бретт (сентябрь 2020 г.). «Популяция ретроградных нерегулярных лун Юпитера километрового масштаба». Журнал планетарной науки . 1 (2): 52. arXiv : 2009.03382 . Bibcode : 2020PSJ.....1...52A. doi : 10.3847/PSJ/abad95 . S2CID 221534456.
- ^ На основе определений из Оксфордского словаря астрономии , ISBN 0-19-211596-0
- ^ abc Grav, Tommy; Holman, Matthew J.; Gladman, Brett J.; Aksnes, Kaare (2003). "Фотометрическое исследование нерегулярных спутников". Icarus . 166 (1): 33–45. arXiv : astro-ph/0301016 . Bibcode :2003Icar..166...33G. doi :10.1016/j.icarus.2003.07.005. S2CID 7793999.
- ^ abc Grav, Tommy; Holman, Matthew J. ; Fraser, Wesley C. (2004-09-20). "Фотометрия нерегулярных спутников Урана и Нептуна". The Astrophysical Journal . 613 (1): L77–L80. arXiv : astro-ph/0405605 . Bibcode :2004ApJ...613L..77G. doi :10.1086/424997. S2CID 15706906.
- ^ ab Nesvorn, David; Beaug, Cristian; Dones, Luke (2004). "Collisional Origin of Families of Irregular Satellites" (PDF) . The Astronomical Journal . 127 (3): 1768–1783. Bibcode :2004AJ....127.1768N. doi :10.1086/382099. S2CID 27293848. Архивировано (PDF) из оригинала 2017-08-09 . Получено 2006-08-02 .
- ^ ab Grav, Tommy; Holman, Matthew J. (2004). «Ближняя инфракрасная фотометрия нерегулярных спутников Юпитера и Сатурна». The Astrophysical Journal . 605 (2): L141–L144. arXiv : astro-ph/0312571 . Bibcode : 2004ApJ...605L.141G. doi : 10.1086/420881. S2CID 15665146.
- ^ Sheppard, SS; Jewitt, DC (2003). "Обильная популяция малых нерегулярных спутников вокруг Юпитера" (PDF) . Nature . 423 (6937): 261–263. Bibcode :2003Natur.423..261S. doi :10.1038/nature01584. PMID 12748634. S2CID 4424447. Архивировано (PDF) из оригинала 2013-10-15 . Получено 2015-08-29 .
- ^ Шеппард, СС; Джуитт, Д.; Клейна, Дж. (2005). «Сверхглубокое исследование нерегулярных спутников Урана: пределы полноты». The Astronomical Journal . 129 (1): 518–525. arXiv : astro-ph/0410059 . Bibcode : 2005AJ....129..518S. doi : 10.1086/426329. S2CID 18688556.
- ^ Шеппард, Скотт С .; Джуитт, Дэвид К .; Клейна, Ян (2006). «Обзор «нормальных» нерегулярных спутников вокруг Нептуна: пределы полноты». The Astronomical Journal . 132 (1): 171–176. arXiv : astro-ph/0604552 . Bibcode : 2006AJ....132..171S. doi : 10.1086/504799. S2CID 154011.
- ^ Холман, М. Дж. ; Кавелаарс, Дж. Дж. ; Грав, Т.; и др. (2004). «Открытие пяти нерегулярных лун Нептуна» (PDF) . Nature . 430 (7002): 865–867. Bibcode :2004Natur.430..865H. doi :10.1038/nature02832. PMID 15318214. S2CID 4412380. Архивировано (PDF) из оригинала 2 ноября 2013 г. Получено 24 октября 2011 г.
- ^ Эндрю Джонс (21.12.2023). «Планы Китая по исследованию внешней Солнечной системы». Планетарное общество . Получено 27.12.2023 .
Внешние ссылки
- Страницы Дэвида Джуитта
- Обстоятельства открытия от JPL
- Средние орбитальные элементы от JPL
- MPC: Служба эфемерид естественных спутников
- Тильманн Денк: Внешние спутники Юпитера и Сатурна