Интерферометрия
Интерферометрия — это метод, который использует интерференцию наложенных волн для извлечения информации. [1] Интерферометрия обычно использует электромагнитные волны и является важным методом исследования в области астрономии , волоконной оптики , инженерной метрологии , оптической метрологии, океанографии , сейсмологии , спектроскопии (и ее приложений к химии ), квантовой механики , ядерной физики и физики элементарных частиц , физики плазмы , биомолекулярных взаимодействий , поверхностного профилирования, микрофлюидики , измерения механических напряжений/деформаций, велосиметрии , оптометрии и создания голограмм . [2] : 1–2
Интерферометры — это устройства, которые извлекают информацию из интерференции. Они широко используются в науке и промышленности для измерения микроскопических смещений, изменений показателя преломления и неровностей поверхности. В случае большинства интерферометров свет от одного источника разделяется на два луча, которые движутся по разным оптическим путям , которые затем снова объединяются для создания интерференции; два некогерентных источника также могут интерферировать при некоторых обстоятельствах. [3] Полученные интерференционные полосы дают информацию о разнице в длинах оптических путей . В аналитической науке интерферометры используются для измерения длин и формы оптических компонентов с нанометровой точностью; они являются самыми точными из существующих приборов для измерения длины. В спектроскопии с преобразованием Фурье они используются для анализа света, содержащего особенности поглощения или испускания, связанные с веществом или смесью. Астрономический интерферометр состоит из двух или более отдельных телескопов, которые объединяют свои сигналы, предлагая разрешение, эквивалентное разрешению телескопа с диаметром, равным наибольшему расстоянию между его отдельными элементами.
Основные принципы

Интерферометрия использует принцип суперпозиции для объединения волн таким образом, что результат их объединения будет иметь некоторое значимое свойство, которое является диагностическим для исходного состояния волн. Это работает, потому что когда объединяются две волны с одинаковой частотой , результирующая картина интенсивности определяется разностью фаз между двумя волнами — волны, которые находятся в фазе, будут подвергаться конструктивной интерференции, в то время как волны, которые находятся в противофазе, будут подвергаться деструктивной интерференции. Волны, которые не полностью находятся в фазе или не полностью в противофазе, будут иметь промежуточную картину интенсивности, которая может быть использована для определения их относительной разности фаз. Большинство интерферометров используют свет или некоторую другую форму электромагнитной волны . [2] : 3–12
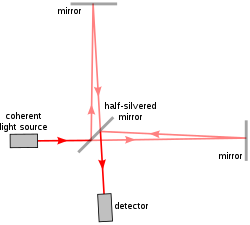
Обычно (см. рис. 1, хорошо известную конфигурацию Майкельсона) один входящий луч когерентного света будет разделен на два идентичных луча с помощью светоделителя ( частично отражающего зеркала). Каждый из этих лучей проходит свой путь, называемый путем, и они рекомбинируются перед тем, как достичь детектора. Разница в пути, разница в расстоянии, пройденном каждым лучом, создает разницу фаз между ними. Именно эта введенная разница фаз создает интерференционную картину между изначально идентичными волнами. [2] : 14–17 Если один луч был разделен по двум путям, то разница фаз является диагностическим признаком всего, что изменяет фазу вдоль путей. Это может быть физическое изменение самой длины пути или изменение показателя преломления вдоль пути. [2] : 93–103
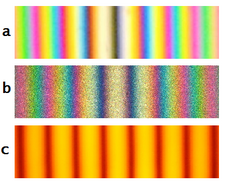
Как видно на рис. 2а и 2б, наблюдатель имеет прямой вид на зеркало M 1 , увиденное через светоделитель, и видит отраженное изображение M ′ 2 зеркала M 2 . Полосы можно интерпретировать как результат интерференции между светом, исходящим от двух виртуальных изображений S ′ 1 и S ′ 2 исходного источника S . Характеристики интерференционной картины зависят от природы источника света и точной ориентации зеркал и светоделителя. На рис. 2а оптические элементы ориентированы таким образом, что S ′ 1 и S ′ 2 находятся на одной линии с наблюдателем, и результирующая интерференционная картина состоит из окружностей, центрированных на нормали к M 1 и M' 2 . Если, как на рис. 2b, M 1 и M ′ 2 наклонены относительно друг друга, интерференционные полосы, как правило, будут иметь форму конических сечений (гипербол), но если M ′ 1 и M ′ 2 перекрываются, полосы вблизи оси будут прямыми, параллельными и равномерно распределенными. Если S является протяженным источником, а не точечным, как показано, полосы рис. 2a должны наблюдаться с помощью телескопа, установленного на бесконечности, в то время как полосы рис. 2b будут локализованы на зеркалах. [2] : 17
Использование белого света приведет к образованию узора из цветных полос (см. рис. 3). [2] : 26 Центральная полоса, представляющая равную длину пути, может быть светлой или темной в зависимости от количества инверсий фазы, испытываемых двумя лучами при прохождении через оптическую систему. [2] : 26, 171–172 (См. обсуждение этого вопроса в разделе Интерферометр Майкельсона .)
История
Закон интерференции света был описан Томасом Юнгом в его Бейкерианской лекции 1803 года в Королевском обществе Лондона. [4] Готовясь к лекции, Юнг провел эксперимент с двумя апертурами, который продемонстрировал интерференционные полосы. Его интерпретация в терминах интерференции волн была отвергнута большинством ученых того времени из-за доминирования корпускулярной теории света Исаака Ньютона, предложенной столетием ранее. [5]
Французский инженер Огюстен Жан Френель , не зная о результатах Юнга, начал работать над волновой теорией света и интерференции и был представлен Франсуа Араго . Между 1816 и 1818 годами Френель и Араго проводили эксперименты по интерференции в Парижской обсерватории. В это время Араго спроектировал и построил первый интерферометр, используя его для измерения показателя преломления влажного воздуха относительно сухого воздуха, что представляло потенциальную проблему для астрономических наблюдений за положением звезд. [6] Успех волновой теории света Френеля был подтвержден в его отмеченном наградой мемуаре 1819 года, в котором были предсказаны и измерены дифракционные картины. Интерферометр Араго позже был использован в 1850 году Леоном Фуко для измерения скорости света в воздухе относительно воды, и он был снова использован в 1851 году Ипполитом Физо для измерения эффекта сопротивления Френеля на скорость света в движущейся воде. [7]
Жюль Жамен разработал первый однолучевой интерферометр (не требующий разделительной апертуры, как интерферометр Араго) в 1856 году. В 1881 году американский физик Альберт А. Михельсон , посещая Германа фон Гельмгольца в Берлине, изобрел интерферометр, названный в его честь, интерферометр Михельсона , для поиска эффектов движения Земли на скорость света. Нулевые результаты Майкельсона, полученные в подвале Потсдамской обсерватории за пределами Берлина (движение лошадей в центре Берлина создавало слишком много вибраций), и его более поздние более точные нулевые результаты, полученные совместно с Эдвардом У. Морли в колледже Кейса в Кливленде, штат Огайо, способствовали растущему кризису светоносного эфира. Эйнштейн утверждал, что именно измерение Физо скорости света в движущейся воде с использованием интерферометра Араго вдохновило его теорию релятивистского сложения скоростей. [8]
Категории
Интерферометры и интерферометрические методы можно классифицировать по ряду критериев:
Гомодинное и гетеродинное обнаружение
При гомодинном детектировании интерференция происходит между двумя лучами на одной и той же длине волны (или несущей частоте ). Разность фаз между двумя лучами приводит к изменению интенсивности света на детекторе. Результирующая интенсивность света после смешивания этих двух лучей измеряется, или просматривается или регистрируется картина интерференционных полос. [9] Большинство интерферометров, обсуждаемых в этой статье, попадают в эту категорию.
Метод гетеродина используется для (1) сдвига входного сигнала в новый частотный диапазон, а также (2) усиления слабого входного сигнала (предполагая использование активного смесителя ). Слабый входной сигнал частоты f 1 смешивается с сильной опорной частотой f 2 от гетеродина (LO). Нелинейная комбинация входных сигналов создает два новых сигнала, один на сумме f 1 + f 2 двух частот, а другой на разности f 1 − f 2 . Эти новые частоты называются гетеродинами . Обычно требуется только одна из новых частот, а другой сигнал отфильтровывается из выхода смесителя. Выходной сигнал будет иметь интенсивность, пропорциональную произведению амплитуд входных сигналов. [9]
Наиболее важным и широко используемым применением гетеродинной техники является супергетеродинный приемник (superhet), изобретенный в 1917-18 годах американским инженером Эдвином Говардом Армстронгом и французским инженером Люсьеном Леви . В этой схеме входящий радиочастотный сигнал от антенны смешивается с сигналом от локального генератора (LO) и преобразуется с помощью гетеродинной техники в сигнал с более низкой фиксированной частотой, называемый промежуточной частотой (IF). Эта IF усиливается и фильтруется, прежде чем подается на детектор , который извлекает аудиосигнал, который отправляется на громкоговоритель. [10]
Оптическое гетеродинное обнаружение является расширением гетеродинного метода на более высокие (видимые) частоты. [9] Хотя оптическая гетеродинная интерферометрия обычно выполняется в одной точке, также возможно выполнение этого широкополосного метода. [11]
Двойной путь против общего пути

Двухпутевой интерферометр — это тот, в котором опорный луч и луч образца движутся по расходящимся путям. Примерами служат интерферометр Майкельсона , интерферометр Тваймана–Грина и интерферометр Маха–Цендера . После возмущения взаимодействием с исследуемым образцом луч образца рекомбинируется с опорным лучом, создавая интерференционную картину, которую затем можно интерпретировать. [2] : 13–22
Интерферометр с общим путем — это класс интерферометров, в которых опорный луч и луч образца движутся по одному и тому же пути. Рис. 4 иллюстрирует интерферометр Саньяка , волоконно-оптический гироскоп , точечный дифракционный интерферометр и интерферометр с боковым сдвигом . Другие примеры интерферометров с общим путем включают фазово-контрастный микроскоп Цернике , бипризму Френеля , нулевой площади Саньяка и интерферометр с рассеивающей пластиной . [12]
Разделение волнового фронта и разделение амплитуды
Инферометры с расщеплением волнового фронта
Интерферометр с расщеплением волнового фронта разделяет световой волновой фронт, выходящий из точки или узкой щели ( т. е. пространственно когерентный свет), и, после того как две части волнового фронта пройдут по разным путям, позволяет им рекомбинировать. [13] Рис. 5 иллюстрирует эксперимент Юнга с интерференцией и зеркало Ллойда . Другие примеры интерферометра с расщеплением волнового фронта включают бипризму Френеля, би-линзу Билле, интерферометр Майкельсона с дифракционной решеткой, [14] и интерферометр Рэлея . [15]
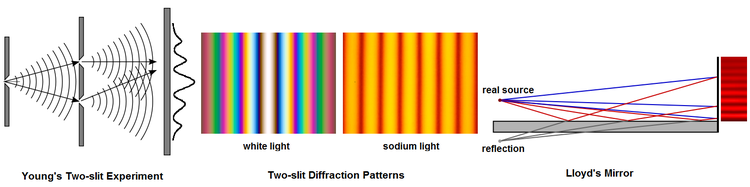
В 1803 году интерференционный эксперимент Юнга сыграл важную роль в общем принятии волновой теории света. Если в эксперименте Юнга используется белый свет, результатом является белая центральная полоса конструктивной интерференции, соответствующая равной длине пути от двух щелей, окруженная симметричным рисунком цветных полос уменьшающейся интенсивности. В дополнение к непрерывному электромагнитному излучению эксперимент Юнга был проведен с отдельными фотонами, [16] с электронами, [17] [18] и с молекулами бакибола, достаточно большими, чтобы их можно было увидеть под электронным микроскопом . [19]
Зеркало Ллойда генерирует интерференционные полосы, объединяя прямой свет от источника (синие линии) и свет от отраженного изображения источника (красные линии) от зеркала, удерживаемого при скользящем падении. Результатом является асимметричный рисунок полос. Полоса равной длины пути, ближайшая к зеркалу, темная, а не яркая. В 1834 году Хамфри Ллойд интерпретировал этот эффект как доказательство того, что фаза луча, отраженного от передней поверхности, инвертирована. [20] [21]
Инферометры с разделением амплитуды
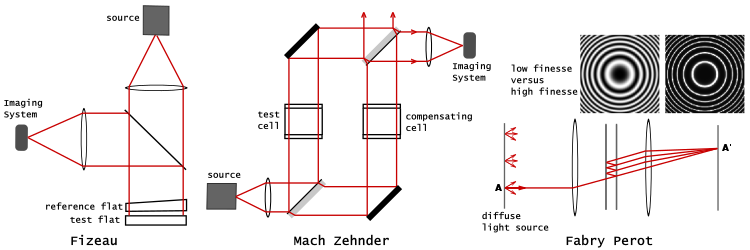
Интерферометр с разделением амплитуды использует частичный отражатель для разделения амплитуды падающей волны на отдельные лучи, которые разделяются и рекомбинируются.
Интерферометр Физо показан в том виде, в котором он может быть настроен для проверки оптической плоскости . Точно вырезанная эталонная плоскость помещается поверх тестируемой плоскости, разделенная узкими прокладками. Эталонная плоскость слегка скошена (необходима лишь доля градуса скоса), чтобы предотвратить образование интерференционных полос на задней поверхности плоскости. Разделение тестовой и эталонной плоскостей позволяет наклонять две плоскости относительно друг друга. Регулируя наклон, который добавляет контролируемый фазовый градиент к рисунку полос, можно контролировать расстояние и направление полос, так что можно получить легко интерпретируемую серию почти параллельных полос, а не сложный вихрь контурных линий. Однако разделение пластин требует, чтобы освещающий свет был коллимирован. На рис. 6 показан коллимированный пучок монохроматического света, освещающий две плоскости, и светоделитель, позволяющий просматривать полосы на оси. [22] [23]
Интерферометр Маха-Цендера является более универсальным инструментом, чем интерферометр Майкельсона. Каждый из хорошо разделенных световых путей проходится только один раз, и полосы можно настроить так, чтобы они были локализованы в любой желаемой плоскости. [2] : 18 Обычно полосы настраиваются так, чтобы они лежали в той же плоскости, что и тестовый объект, так что полосы и тестовый объект можно фотографировать вместе. Если решено создавать полосы в белом свете, то, поскольку белый свет имеет ограниченную длину когерентности , порядка микрометров , необходимо проявить большую осторожность, чтобы выровнять оптические пути, иначе полосы не будут видны. Как показано на рис. 6, компенсирующая ячейка будет помещена на пути опорного луча, чтобы соответствовать тестовой ячейке. Обратите также внимание на точную ориентацию расщепителей луча. Отражающие поверхности расщепителей луча будут ориентированы так, чтобы тестовый и опорный лучи проходили через равное количество стекла. В этой ориентации тестовый и опорный лучи испытывают по два отражения от передней поверхности, что приводит к одинаковому числу инверсий фазы. В результате свет, проходящий равную оптическую длину пути в тестовом и опорном лучах, создает белую световую полосу конструктивной интерференции. [24] [25]
Сердцем интерферометра Фабри–Перо является пара частично посеребренных стеклянных оптических плоских пластин, расположенных на расстоянии от нескольких миллиметров до сантиметров друг от друга, причем посеребренные поверхности обращены друг к другу. (В качестве альтернативы эталон Фабри–Перо использует прозрачную пластину с двумя параллельными отражающими поверхностями.) [2] : 35–36 Как и в интерферометре Физо, плоскости слегка скошены. В типичной системе освещение обеспечивается диффузным источником, установленным в фокальной плоскости коллимирующей линзы. Фокусирующая линза создает то, что было бы перевернутым изображением источника, если бы парных плоскостей не было, т. е. при отсутствии парных плоскостей весь свет, излучаемый из точки A, проходящий через оптическую систему, был бы сфокусирован в точке A'. На рис. 6 прослеживается только один луч, излучаемый из точки A на источнике. Когда луч проходит через парные плоскости, он многократно отражается, создавая несколько пропущенных лучей, которые собираются фокусирующей линзой и переносятся в точку A' на экране. Полная интерференционная картина принимает вид набора концентрических колец. Резкость колец зависит от отражательной способности плоскостей. Если отражательная способность высока, что приводит к высокому коэффициенту добротности (т. е. высокой четкости), монохроматический свет создает набор узких ярких колец на темном фоне. [26] На рис. 6 изображение с низкой четкостью соответствует отражательной способности 0,04 (т. е. непосеребренным поверхностям) по сравнению с отражательной способностью 0,95 для изображения с высокой четкостью.
Рис. 6 иллюстрирует интерферометры Физо, Маха-Цендера и Фабри-Перо. Другие примеры интерферометров с амплитудным расщеплением включают интерферометры Майкельсона , Тваймана-Грина , лазерного неравного пути и Линника . [27]
Майкельсон-Морли
Майкельсон и Морли (1887) [28] и другие ранние экспериментаторы, использовавшие интерферометрические методы в попытке измерить свойства светоносного эфира , использовали монохроматический свет только для первоначальной настройки своего оборудования, всегда переключаясь на белый свет для фактических измерений. Причина в том, что измерения регистрировались визуально. Монохроматический свет привел бы к однородному узору полос. Не имея современных средств контроля температуры окружающей среды , экспериментаторы боролись с непрерывным дрейфом полос, даже если интерферометр мог быть установлен в подвале. Поскольку полосы иногда исчезали из-за вибраций от проезжающего конного транспорта, далеких гроз и тому подобного, наблюдателю было бы легко «потеряться», когда полосы снова стали видимыми. Преимущества белого света, который создавал характерный цветной узор полос, намного перевешивали трудности выравнивания аппарата из-за его низкой длины когерентности . [29] Это был ранний пример использования белого света для разрешения «неоднозначности 2 пи».
Приложения
Физика и астрономия
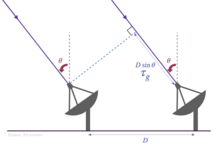
В физике одним из важнейших экспериментов конца 19 века был знаменитый «неудавшийся эксперимент» Майкельсона и Морли , который предоставил доказательства специальной теории относительности . Недавние повторения эксперимента Майкельсона–Морли выполняют гетеродинные измерения частот биений скрещенных криогенных оптических резонаторов . Рис. 7 иллюстрирует эксперимент с резонатором, проведенный Мюллером и др. в 2003 году. [30] Два оптических резонатора, изготовленных из кристаллического сапфира, контролирующих частоты двух лазеров, были установлены под прямым углом внутри гелиевого криостата. Частотный компаратор измерял частоту биений объединенных выходов двух резонаторов. По состоянию на 2009 год [обновлять]точность, с которой анизотропия скорости света может быть исключена в экспериментах с резонатором, находится на уровне 10−17 . [ 31] [32]
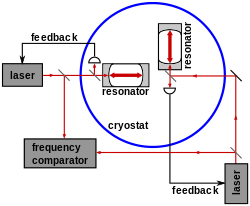 Рисунок 7. Эксперимент Майкельсона–Морли с криогенными оптическими резонаторами | 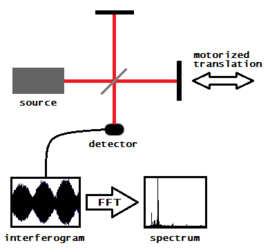 Рисунок 8. Фурье-спектроскопия | Рисунок 9. Фотография солнечной короны, полученная с помощью коронографа LASCO C1. |
Интерферометры Майкельсона используются в настраиваемых узкополосных оптических фильтрах [33] и в качестве основного аппаратного компонента спектрометров с преобразованием Фурье . [34]
При использовании в качестве настраиваемого узкополосного фильтра интерферометры Майкельсона демонстрируют ряд преимуществ и недостатков по сравнению с конкурирующими технологиями, такими как интерферометры Фабри–Перо или фильтры Лио . Интерферометры Майкельсона имеют наибольшее поле зрения для заданной длины волны и относительно просты в эксплуатации, поскольку настройка осуществляется посредством механического вращения волновых пластин, а не посредством управления высоким напряжением пьезоэлектрических кристаллов или оптических модуляторов на основе ниобата лития, как в системе Фабри–Перо. По сравнению с фильтрами Лио, которые используют двулучепреломляющие элементы, интерферометры Майкельсона имеют относительно низкую температурную чувствительность. С другой стороны, интерферометры Майкельсона имеют относительно ограниченный диапазон длин волн и требуют использования предварительных фильтров, которые ограничивают пропускание. [35]
Рис. 8 иллюстрирует работу спектрометра с преобразованием Фурье, который по сути является интерферометром Майкельсона с одним подвижным зеркалом. (Практический спектрометр с преобразованием Фурье заменил бы плоские зеркала обычного интерферометра Майкельсона на уголковые кубические отражатели, но для простоты на рисунке это не показано.) Интерферограмма генерируется путем проведения измерений сигнала во многих дискретных положениях подвижного зеркала. Преобразование Фурье преобразует интерферограмму в фактический спектр. [36]
На рис. 9 показано доплеровское изображение солнечной короны, полученное с помощью настраиваемого интерферометра Фабри-Перо для восстановления сканов солнечной короны на ряде длин волн вблизи зеленой линии FeXIV. Изображение представляет собой цветное изображение доплеровского смещения линии, которое может быть связано со скоростью корональной плазмы по направлению к спутниковой камере или от нее.
Тонкопленочные эталоны Фабри–Перо используются в узкополосных фильтрах, способных выбирать одну спектральную линию для получения изображения; например, линию H-альфа или линию Ca-K Солнца или звезд. На рис. 10 показано изображение Солнца, полученное с помощью телескопа EIT в экстремальном ультрафиолетовом диапазоне (EIT) при 195 ангстрем (19,5 нм), что соответствует спектральной линии многократно ионизированных атомов железа. [37] EIT использовал многослойные покрытые отражающие зеркала, которые были покрыты чередующимися слоями легкого «разделительного» элемента (например, кремния) и тяжелого «рассеивающего» элемента (например, молибдена). На каждом зеркале было размещено около 100 слоев каждого типа толщиной около 10 нм каждый. Толщина слоев строго контролировалась, так что на желаемой длине волны отраженные фотоны от каждого слоя интерферировали конструктивно.
Лазерная интерферометрическая гравитационно-волновая обсерватория (LIGO) использует два 4-километровых интерферометра Майкельсона–Фабри–Перо для обнаружения гравитационных волн . [38] В этом приложении резонатор Фабри–Перо используется для хранения фотонов в течение почти миллисекунды, пока они отскакивают вверх и вниз между зеркалами. Это увеличивает время, в течение которого гравитационная волна может взаимодействовать со светом, что приводит к лучшей чувствительности на низких частотах. Меньшие резонаторы, обычно называемые очистителями мод, используются для пространственной фильтрации и стабилизации частоты основного лазера. Первое наблюдение гравитационных волн произошло 14 сентября 2015 года. [39]
Относительно большое и свободно доступное рабочее пространство интерферометра Маха-Цендера, а также его гибкость в определении положения полос сделали его интерферометром выбора для визуализации потока в аэродинамических трубах, [40] [41] и для исследований визуализации потока в целом. Он часто используется в областях аэродинамики, физики плазмы и теплопередачи для измерения давления, плотности и изменений температуры в газах. [2] : 18, 93–95
Интерферометры Маха-Цендера также используются для изучения одного из самых противоречивых предсказаний квантовой механики, явления, известного как квантовая запутанность . [42] [43]

Астрономический интерферометр позволяет получать наблюдения с высоким разрешением, используя технику синтеза апертуры , смешивая сигналы от кластера сравнительно небольших телескопов, а не от одного очень дорогого монолитного телескопа. [44]
Ранние интерферометры радиотелескопов использовали одну базовую линию для измерения. Более поздние астрономические интерферометры, такие как Very Large Array, показанный на рис. 11, использовали массивы телескопов, расположенных в определенном порядке на земле. Ограниченное количество базовых линий приведет к недостаточному покрытию. Это было устранено путем использования вращения Земли для вращения массива относительно неба. Таким образом, одна базовая линия могла измерять информацию в нескольких ориентациях, выполняя повторные измерения, метод, называемый синтезом вращения Земли . Базовые линии длиной в тысячи километров были получены с помощью интерферометрии с очень длинной базовой линией . [44]

Астрономическая оптическая интерферометрия должна была преодолеть ряд технических проблем, которых не было в радиотелескопической интерферометрии. Короткие длины волн света требуют чрезвычайной точности и стабильности конструкции. Например, пространственное разрешение в 1 угловую миллисекунду требует стабильности 0,5 мкм на 100-метровой базовой линии. Оптические интерферометрические измерения требуют высокочувствительных малошумящих детекторов, которые не были доступны до конца 1990-х годов. Астрономическое «видение» , турбулентность, которая заставляет звезды мерцать, вносит быстрые случайные изменения фазы во входящий свет, требуя, чтобы скорость сбора данных была выше скорости турбулентности. [46] [47] Несмотря на эти технические трудности, в настоящее время действуют три основных объекта, предлагающих разрешения вплоть до дробного диапазона угловых миллисекунд. Это связанное видео показывает фильм, собранный из изображений синтеза апертуры системы Бета Лиры , двойной звездной системы примерно в 960 световых годах (290 парсеков) от нас в созвездии Лиры, как это наблюдалось массивом CHARA с инструментом MIRC. Более яркий компонент - это первичная звезда, или донор массы. Более слабый компонент - это толстый диск, окружающий вторичную звезду, или прирост массы. Два компонента разделены 1 миллисекундой дуги. Приливные искажения донора массы и прироста массы отчетливо видны. [48]
Волновой характер материи может быть использован для создания интерферометров. Первыми примерами интерферометров материи были электронные интерферометры , за которыми последовали нейтронные интерферометры . Около 1990 года были продемонстрированы первые атомные интерферометры , за которыми последовали интерферометры, использующие молекулы. [49] [50] [51]
Электронная голография — это метод получения изображений, который фотографически регистрирует картину интерференции электронов объекта, которая затем реконструируется для получения значительно увеличенного изображения исходного объекта. [52] Этот метод был разработан для обеспечения большего разрешения в электронной микроскопии, чем это возможно при использовании обычных методов получения изображений. Разрешение обычной электронной микроскопии ограничено не длиной волны электронов, а большими аберрациями электронных линз. [53]
Нейтронная интерферометрия использовалась для исследования эффекта Ааронова-Бома , для изучения эффектов гравитации, действующих на элементарную частицу, и для демонстрации странного поведения фермионов , которое лежит в основе принципа исключения Паули : в отличие от макроскопических объектов, когда фермионы поворачиваются на 360° вокруг любой оси, они не возвращаются в свое исходное состояние, а приобретают знак минус в своей волновой функции. Другими словами, фермион должен повернуться на 720°, прежде чем вернуться в свое исходное состояние. [54]
Методы атомной интерферометрии достигают достаточной точности, чтобы позволить проводить лабораторные испытания общей теории относительности . [55]
Интерферометры используются в физике атмосферы для высокоточных измерений следовых газов посредством дистанционного зондирования атмосферы. Существует несколько примеров интерферометров, которые используют либо абсорбционные, либо эмиссионные характеристики следовых газов. Типичным применением будет непрерывный мониторинг концентрации столба следовых газов, таких как озон и оксид углерода, над прибором. [56]
Инженерное дело и прикладная наука


Интерферометрия Ньютона (испытательная пластина) часто используется в оптической промышленности для проверки качества поверхностей по мере их формования и обработки. На рис. 13 показаны фотографии контрольных плоских поверхностей, используемых для проверки двух контрольных плоских поверхностей на разных стадиях завершения, демонстрирующие различные узоры интерференционных полос. Контрольные плоские поверхности покоятся, их нижние поверхности соприкасаются с контрольными плоскостями, и они освещаются монохроматическим источником света. Световые волны, отраженные от обеих поверхностей, интерферируют, в результате чего образуется узор из ярких и темных полос. Поверхность на левой фотографии почти плоская, на что указывает узор из прямых параллельных интерференционных полос с равными интервалами. Поверхность на правой фотографии неровная, в результате чего образуется узор из изогнутых полос. Каждая пара соседних полос представляет собой разницу в высоте поверхности в половину длины волны используемого света, поэтому разницу в высоте можно измерить, подсчитав полосы. Плоскостность поверхностей можно измерить с точностью до миллионных долей дюйма этим методом. Чтобы определить, является ли тестируемая поверхность вогнутой или выпуклой по отношению к эталонной оптической плоскости, можно применить любую из нескольких процедур. Можно наблюдать, как полосы смещаются, если слегка нажать на верхнюю плоскость. Если наблюдать полосы в белом свете, последовательность цветов становится знакомой с опытом и помогает в интерпретации. Наконец, можно сравнить внешний вид полос, когда человек перемещает голову из нормального положения в наклонное положение для просмотра. [57] Такого рода маневры, хотя и распространены в оптическом магазине, не подходят для формальной испытательной среды. Когда плоскости готовы к продаже, их обычно устанавливают в интерферометре Физо для формального тестирования и сертификации.
Эталоны Фабри-Перо широко используются в телекоммуникациях , лазерах и спектроскопии для контроля и измерения длин волн света. Дихроичные фильтры представляют собой многослойные тонкопленочные эталоны. В телекоммуникациях мультиплексирование с разделением по длине волны , технология, которая позволяет использовать несколько длин волн света через одно оптическое волокно, зависит от фильтрующих устройств, которые представляют собой тонкопленочные эталоны. Одномодовые лазеры используют эталоны для подавления всех оптических мод резонатора, кроме одной интересующей. [2] : 42
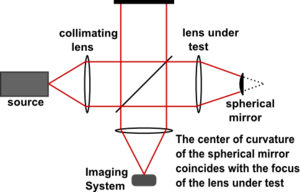
Интерферометр Тваймана–Грина, изобретенный Твайманом и Грином в 1916 году, является вариантом интерферометра Майкельсона, широко используемого для тестирования оптических компонентов. [58] Основными характеристиками, отличающими его от конфигурации Майкельсона, являются использование монохроматического точечного источника света и коллиматора. Майкельсон (1918) критиковал конфигурацию Тваймана–Грина как непригодную для тестирования больших оптических компонентов, поскольку доступные в то время источники света имели ограниченную длину когерентности . Майкельсон указал, что ограничения на геометрию, вызванные ограниченной длиной когерентности, требуют использования опорного зеркала того же размера, что и тестовое зеркало, что делает Твайман–Грина непрактичным для многих целей. [59] Спустя десятилетия появление лазерных источников света ответило на возражения Майкельсона. (Интерферометр Тваймана–Грина, использующий лазерный источник света и неравную длину пути, известен как лазерный интерферометр неравного пути, или LUPI.) На рис. 14 показан интерферометр Тваймана–Грина, установленный для проверки линзы. Свет от монохроматического точечного источника расширяется рассеивающей линзой (не показана), затем коллимируется в параллельный пучок. Выпуклое сферическое зеркало располагается так, чтобы его центр кривизны совпадал с фокусом тестируемой линзы. Выходящий пучок регистрируется системой визуализации для анализа. [60]
Интерферометры Маха-Цендера используются в интегральных оптических схемах , в которых свет интерферирует между двумя ветвями волновода , которые модулируются извне для изменения их относительной фазы. Небольшой наклон одного из светоделителей приведет к разнице хода и изменению интерференционной картины. Интерферометры Маха-Цендера являются основой самых разных устройств, от радиочастотных модуляторов до датчиков [61] [62] и оптических переключателей . [63]
Последние предложенные чрезвычайно большие астрономические телескопы , такие как Тридцатиметровый телескоп и Чрезвычайно большой телескоп , будут иметь сегментированную конструкцию. Их главные зеркала будут построены из сотен шестиугольных зеркальных сегментов. Полировка и обработка этих высокоасферических и невращательно симметричных зеркальных сегментов представляет собой серьезную проблему. Традиционные средства оптического тестирования сравнивают поверхность со сферическим эталоном с помощью нулевого корректора . В последние годы компьютерные голограммы (CGH) начали дополнять нулевые корректоры в испытательных установках для сложных асферических поверхностей. Рис. 15 иллюстрирует, как это делается. В отличие от рисунка, фактические CGH имеют межстрочный интервал порядка 1–10 мкм. Когда лазерный свет проходит через CGH, дифрагированный луч нулевого порядка не испытывает никаких изменений волнового фронта. Однако волновой фронт дифрагированного луча первого порядка изменяется, чтобы соответствовать желаемой форме тестовой поверхности. В показанной тестовой установке интерферометра Физо дифрагированный луч нулевого порядка направляется к сферической опорной поверхности, а дифрагированный луч первого порядка направляется к тестовой поверхности таким образом, что два отраженных луча объединяются, образуя интерференционные полосы. Для самых внутренних зеркал можно использовать ту же тестовую установку, что и для самых внешних, при этом необходимо заменить только CGH. [64]

Кольцевые лазерные гироскопы (RLG) и волоконно-оптические гироскопы (FOG) являются интерферометрами, используемыми в навигационных системах. Они работают по принципу эффекта Саньяка . Различие между RLG и FOG заключается в том, что в RLG все кольцо является частью лазера, тогда как в FOG внешний лазер вводит встречные лучи в оптоволоконное кольцо, а вращение системы затем вызывает относительный фазовый сдвиг между этими лучами. В RLG наблюдаемый фазовый сдвиг пропорционален накопленному вращению, тогда как в FOG наблюдаемый фазовый сдвиг пропорционален угловой скорости. [65]
В телекоммуникационных сетях гетеродинирование используется для перемещения частот отдельных сигналов в разные каналы, которые могут совместно использовать одну физическую линию передачи. Это называется частотным разделением каналов (FDM). Например, коаксиальный кабель, используемый в системе кабельного телевидения, может передавать 500 телевизионных каналов одновременно, поскольку каждому из них присваивается своя частота, поэтому они не мешают друг другу. Доплеровские радарные детекторы непрерывной волны (CW) по сути являются гетеродинными устройствами обнаружения, которые сравнивают переданные и отраженные лучи. [66]
Оптическое гетеродинное обнаружение используется для когерентных доплеровских лидарных измерений, способных обнаруживать очень слабый свет, рассеянный в атмосфере, и контролировать скорость ветра с высокой точностью. Оно применяется в оптоволоконной связи , в различных спектроскопических методах высокого разрешения, а метод самогетеродина может использоваться для измерения ширины линии лазера. [9] [67]
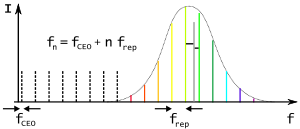
Оптическое гетеродинное детектирование является важным методом, используемым для высокоточных измерений частот оптических источников, а также для стабилизации их частот. Еще сравнительно недавно для соединения микроволновой частоты цезиевого или другого атомного источника времени с оптическими частотами требовались длинные частотные цепи. На каждом шаге цепи использовался бы умножитель частоты для создания гармоники частоты этого шага, которая сравнивалась бы гетеродинным детектированием со следующим шагом (выходом микроволнового источника, дальнего инфракрасного лазера, инфракрасного лазера или видимого лазера). Каждое измерение одной спектральной линии требовало нескольких лет усилий по построению пользовательской частотной цепи. В настоящее время оптические частотные гребенки обеспечивают гораздо более простой метод измерения оптических частот. Если лазер с синхронизированными модами модулируется для формирования последовательности импульсов, его спектр, как видно, состоит из несущей частоты, окруженной близко расположенной гребенкой оптических боковых частот с интервалом, равным частоте повторения импульсов (рис. 16). Частота повторения импульсов привязана к частотному стандарту , а частоты элементов гребенки на красном конце спектра удваиваются и гетеродинируются с частотами элементов гребенки на синем конце спектра, что позволяет гребенке служить своей собственной точкой отсчета. Таким образом, синхронизация выходного сигнала частотной гребенки с атомным стандартом может быть выполнена за один шаг. Для измерения неизвестной частоты выходной сигнал частотной гребенки рассеивается в спектре. Неизвестная частота перекрывается соответствующим спектральным сегментом гребенки, и измеряется частота результирующих гетеродинных биений. [68] [69]
Одним из наиболее распространенных промышленных применений оптической интерферометрии является ее использование в качестве универсального измерительного инструмента для высокоточного исследования топографии поверхности. Популярные методы интерферометрических измерений включают интерферометрию со сдвигом фаз (PSI) [70] и вертикальную сканирующую интерферометрию (VSI) [71] , также известную как сканирующая интерферометрия белого света (SWLI) или по терминологии ISO когерентная сканирующая интерферометрия (CSI) [72] . CSI использует когерентность для расширения диапазона возможностей интерференционной микроскопии. [73] [74] Эти методы широко используются в микроэлектронном и микрооптическом производстве. PSI использует монохроматический свет и обеспечивает очень точные измерения; однако он применим только для очень гладких поверхностей. CSI часто использует белый свет и высокие числовые апертуры, и вместо того, чтобы смотреть на фазу полос, как это делает PSI, ищет наилучшее положение максимального контраста полос или какую-либо другую особенность общего рисунка полос. В своей простейшей форме CSI обеспечивает менее точные измерения, чем PSI, но может использоваться на грубых поверхностях. Некоторые конфигурации CSI, известные также как Enhanced VSI (EVSI), SWLI высокого разрешения или Frequency Domain Analysis (FDA), используют эффекты когерентности в сочетании с фазой интерференции для повышения точности. [75] [76]
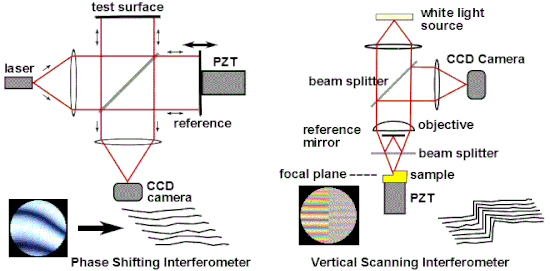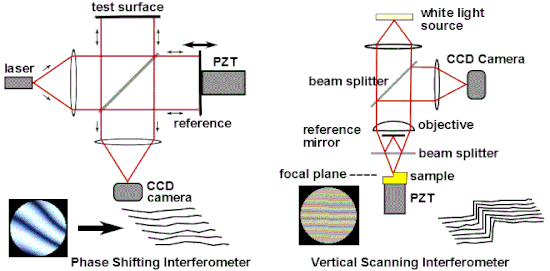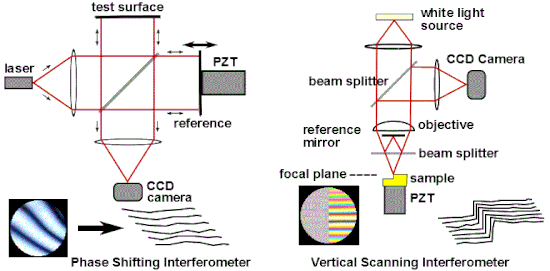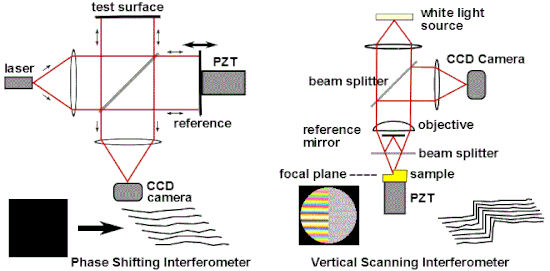
Фазовая интерферометрия решает несколько проблем, связанных с классическим анализом статических интерферограмм. Классически измеряют положение центров полос. Как видно на рис. 13, отклонения полос от прямолинейности и равного расстояния дают меру аберрации. Ошибки в определении положения центров полос обеспечивают неотъемлемый предел точности классического анализа, и любые изменения интенсивности по интерферограмме также внесут ошибку. Существует компромисс между точностью и количеством точек данных: близко расположенные полосы обеспечивают много точек данных низкой точности, в то время как широко расположенные полосы обеспечивают небольшое количество точек данных высокой точности. Поскольку данные о центре полос — это все, что используется в классическом анализе, вся остальная информация, которая теоретически может быть получена путем детального анализа изменений интенсивности в интерферограмме, отбрасывается. [77] [78] Наконец, при использовании статических интерферограмм требуется дополнительная информация для определения полярности волнового фронта: на рис. 13 можно увидеть, что тестируемая поверхность справа отклоняется от плоскости, но по этому единственному изображению нельзя сказать, является ли это отклонение от плоскости вогнутым или выпуклым. Традиционно эта информация была бы получена с использованием неавтоматизированных средств, например, путем наблюдения за направлением движения полос при нажатии на опорную поверхность. [79]
Фазовая интерферометрия преодолевает эти ограничения, не полагаясь на поиск центров полос, а собирая данные об интенсивности из каждой точки датчика изображения ПЗС . Как видно на рис. 17, несколько интерферограмм (по крайней мере три) анализируются с опорной оптической поверхностью, смещенной на точную долю длины волны между каждой экспозицией с помощью пьезоэлектрического преобразователя (PZT). В качестве альтернативы точные фазовые сдвиги могут быть введены путем модуляции частоты лазера. [80] Захваченные изображения обрабатываются компьютером для вычисления ошибок оптического волнового фронта. Точность и воспроизводимость PSI намного выше, чем это возможно при статическом анализе интерферограмм, при этом повторяемость измерений в одну сотую длины волны является обычной. [77] [78] Технология фазового сдвига была адаптирована к различным типам интерферометров, таким как Твайман–Грина, Маха–Цендера, лазерный Физо и даже к обычным конфигурациям пути, таким как точечные дифракционные и интерферометры с боковым сдвигом. [79] [81] В более общем плане методы сдвига фаз можно адаптировать практически к любой системе, использующей полосы для измерения, например, к голографической и спекл-интерферометрии. [79]

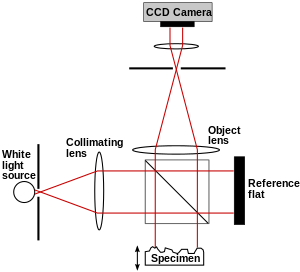
В когерентной сканирующей интерферометрии [ 82] интерференция достигается только тогда, когда задержки длины пути интерферометра совпадают в пределах времени когерентности источника света. CSI контролирует контраст полос, а не фазу полос. [2] : 105 На рис. 17 показан микроскоп CSI, использующий интерферометр Мирау в объективе; другие формы интерферометра, используемые с белым светом, включают интерферометр Майкельсона (для объективов с малым увеличением, где опорное зеркало в объективе Мирау будет прерывать слишком большую часть апертуры) и интерферометр Линника (для объективов с большим увеличением с ограниченным рабочим расстоянием). [83] Образец (или, альтернативно, объектив) перемещается вертикально по всему диапазону высоты образца, и для каждого пикселя находится положение максимального контраста полос. [73] [84] Главное преимущество когерентной сканирующей интерферометрии заключается в том, что можно проектировать системы, которые не страдают от неоднозначности 2 пи когерентной интерферометрии, [85] [86] [87] и, как видно на рис. 18, который сканирует объем 180 мкм x 140 мкм x 10 мкм, он хорошо подходит для профилирования ступеней и шероховатых поверхностей. Осевое разрешение системы частично определяется длиной когерентности источника света. [88] [89] Промышленные приложения включают метрологию поверхности в процессе производства , измерение шероховатости, метрологию поверхности 3D в труднодоступных местах и в агрессивных средах, профилометрию поверхностей с высоким соотношением сторон (канавки, каналы, отверстия) и измерение толщины пленки (полупроводниковая и оптическая промышленность и т. д.). [90] [91]
На рис. 19 показан интерферометр Тваймана–Грина, предназначенный для сканирования макроскопического объекта белым светом.
Голографическая интерферометрия — это метод, который использует голографию для контроля небольших деформаций в реализациях с одной длиной волны. В реализациях с несколькими длинами волн он используется для выполнения размерной метрологии крупных деталей и узлов и для обнаружения более крупных дефектов поверхности. [2] : 111–120
Голографическая интерферометрия была открыта случайно в результате ошибок, допущенных при создании голограмм. Ранние лазеры были относительно слабыми, а фотографические пластины были нечувствительными, что требовало длительных экспозиций, во время которых в оптической системе могли происходить вибрации или мельчайшие сдвиги. Полученные голограммы, показывавшие голографический объект, покрытый полосами, считались испорченными. [92]
В конце концов, несколько независимых групп экспериментаторов в середине 60-х годов поняли, что полосы кодируют важную информацию об изменениях размеров, происходящих в субъекте, и начали намеренно производить голографические двойные экспозиции. Основная статья о голографической интерферометрии охватывает споры о приоритете открытия, которые возникли во время выдачи патента на этот метод. [93]
Двойная и многоэкспозиционная голография — один из трех методов, используемых для создания голографических интерферограмм. Первая экспозиция фиксирует объект в ненапряженном состоянии. Последующие экспозиции на той же фотопластинке производятся, когда объект подвергается некоторому напряжению. Составное изображение отображает разницу между напряженным и ненапряженным состояниями. [94]
Голография в реальном времени — это второй метод создания голографических интерферограмм. Создается голограмма ненапряженного объекта. Эта голограмма освещается опорным лучом для создания голографического изображения объекта, непосредственно наложенного на исходный объект, в то время как объект подвергается некоторому напряжению. Объектные волны из этого голографического изображения будут мешать новым волнам, исходящим от объекта. Эта техника позволяет в реальном времени отслеживать изменения формы. [94]
Третий метод, усредненная по времени голография, заключается в создании голограммы, когда объект подвергается периодическому напряжению или вибрации. Это дает визуальное изображение картины вибрации. [94]
- Рисунок 20. Изображение InSAR вулкана Килауэа, Гавайи, на котором видны полосы, вызванные деформацией рельефа за шестимесячный период.
- Рисунок 21. Полосы ESPI, показывающие режим колебаний зажатой квадратной пластины.
Интерферометрический радиолокатор с синтезированной апертурой (InSAR) — это радиолокационный метод, используемый в геодезии и дистанционном зондировании . Спутниковые радиолокационные изображения географического объекта с синтезированной апертурой снимаются в отдельные дни, и изменения, которые произошли между радиолокационными изображениями, полученными в отдельные дни, регистрируются в виде полос, аналогичных тем, которые получаются в голографической интерферометрии. Этот метод позволяет отслеживать деформации в масштабе от сантиметра до миллиметра, возникающие в результате землетрясений, вулканов и оползней, а также используется в строительной инженерии, в частности для мониторинга проседания и структурной устойчивости. На рис. 20 показан Килауэа, действующий вулкан на Гавайях. Данные, полученные с помощью X-диапазона радиолокатора с синтезированной апертурой космического челнока Endeavour 13 апреля 1994 года и 4 октября 1994 года, использовались для создания интерферометрических полос, которые накладывались на изображение Килауэа, полученное с помощью X-SAR. [95]
Электронная спекл-интерферометрия (ESPI), также известная как телевизионная голография, использует видеодетекцию и запись для получения изображения объекта, на которое накладывается рисунок полос, представляющий смещение объекта между записями. (см. рис. 21) Полосы аналогичны тем, которые получаются в голографической интерферометрии. [2] : 111–120 [96]
Когда лазеры были впервые изобретены, лазерные спеклы считались серьезным недостатком при использовании лазеров для освещения объектов, особенно в голографических изображениях из-за создаваемого зернистого изображения. Позже было обнаружено, что спекл-структуры могут нести информацию о деформациях поверхности объекта. Баттерс и Леендерц разработали технику интерферометрии спекл-структур в 1970 году, [97] и с тех пор спеклы использовались во множестве других приложений. Делается фотография спекл-структуры до деформации, а вторая фотография делается спекл-структуры после деформации. Цифровое вычитание двух изображений приводит к корреляционной картине полос, где полосы представляют собой линии одинаковой деформации. Короткие лазерные импульсы в наносекундном диапазоне могут использоваться для захвата очень быстрых переходных событий. Существует проблема фазы: при отсутствии другой информации невозможно определить разницу между контурными линиями, указывающими на пик, и контурными линиями, указывающими на впадину. Чтобы решить проблему фазовой неоднозначности, ESPI можно объединить с методами сдвига фаз. [98] [99]
Метод установления точных геодезических базовых линий, изобретенный Юрьё Вяйсяля , использовал низкую длину когерентности белого света. Первоначально белый свет разделялся на две части, при этом опорный луч «складывался», отскакивая вперед и назад шесть раз между парой зеркал, расположенных на расстоянии точно 1 м друг от друга. Только если тестовый путь был точно в 6 раз больше опорного пути, можно было увидеть полосы. Повторное применение этой процедуры позволяло точно измерять расстояния до 864 метров. Таким образом установленные базовые линии использовались для калибровки геодезического оборудования для измерения расстояний, что привело к метрологически прослеживаемой шкале для геодезических сетей , измеряемых этими приборами. [100] (Этот метод был заменен GPS.)
Другие применения интерферометров заключались в изучении дисперсии материалов, измерении комплексных показателей преломления и тепловых свойств. Они также используются для трехмерного картирования движения, включая картирование колебательных моделей структур. [75]
Биология и медицина
Оптическая интерферометрия, применяемая в биологии и медицине, обеспечивает чувствительные метрологические возможности для измерения биомолекул, субклеточных компонентов, клеток и тканей. [101] Многие формы биосенсоров без меток основаны на интерферометрии, поскольку прямое взаимодействие электромагнитных полей с локальной молекулярной поляризуемостью устраняет необходимость во флуоресцентных метках или маркерах наночастиц . В большем масштабе клеточная интерферометрия разделяет аспекты фазово-контрастной микроскопии, но включает в себя гораздо больший класс фазово-чувствительных оптических конфигураций, которые основаны на оптической интерференции между клеточными компонентами посредством рефракции и дифракции. В масштабе ткани частично когерентное распространение вперед рассеянного света через микроаберрации и неоднородность структуры ткани дает возможности использовать фазово-чувствительное стробирование (оптическую когерентную томографию), а также фазово-чувствительную флуктуационную спектроскопию для визуализации тонких структурных и динамических свойств.
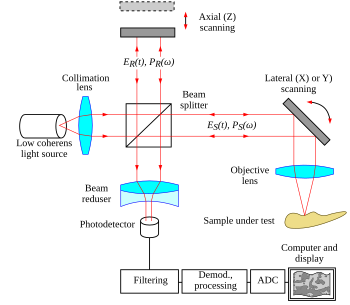 Рисунок 22. Типичная оптическая схема одноточечного ОКТ |  Рисунок 23. Центральная серозная ретинопатия , полученная с помощью оптической когерентной томографии. |
Оптическая когерентная томография (ОКТ) — это метод медицинской визуализации, использующий низкокогерентную интерферометрию для обеспечения томографической визуализации внутренних микроструктур тканей. Как видно на рис. 22, ядром типичной системы ОКТ является интерферометр Майкельсона. Одно плечо интерферометра фокусируется на образце ткани и сканирует образец в продольном растровом шаблоне XY. Другое плечо интерферометра отражается от опорного зеркала. Отраженный свет от образца ткани объединяется с отраженным светом от эталона. Из-за низкой когерентности источника света интерферометрический сигнал наблюдается только на ограниченной глубине образца. Таким образом, сканирование XY регистрирует один тонкий оптический срез образца за раз. Выполняя несколько сканирований, перемещая опорное зеркало между каждым сканированием, можно реконструировать полное трехмерное изображение ткани. [102] [103] Последние достижения стремились объединить нанометровое фазовое извлечение когерентной интерферометрии с возможностью измерения дальности низкокогерентной интерферометрии. [75]
- Рисунок 24. Клетка спирогиры (отделенная от нити водоросли) под фазовым контрастом
- Рисунок 25. Неспорулированная ооциста Toxoplasma gondii , дифференциально-интерференционный контраст
- Рисунок 26. Фазово-контрастное рентгеновское изображение паука высокого разрешения.
Фазовый контраст и дифференциально-интерференционный контраст (ДИК) микроскопия являются важными инструментами в биологии и медицине. Большинство животных клеток и одноклеточных организмов имеют очень мало цвета, а их внутриклеточные органеллы почти полностью невидимы при простом освещении в ярком поле . Эти структуры можно сделать видимыми, окрашивая образцы, но процедуры окрашивания отнимают много времени и убивают клетки. Как видно на рис. 24 и 25, фазовый контраст и ДИК микроскопы позволяют изучать неокрашенные живые клетки. [104] ДИК также имеет небиологические применения, например, при анализе обработки планарных кремниевых полупроводников .
Интерферометрия с низким разрешением по углу (a/LCI) использует рассеянный свет для измерения размеров субклеточных объектов, включая ядра клеток . Это позволяет комбинировать измерения глубины интерферометрии с измерениями плотности. Были обнаружены различные корреляции между состоянием здоровья тканей и измерениями субклеточных объектов. Например, было обнаружено, что по мере того, как ткань изменяется от нормальной к раковой, средний размер ядер клеток увеличивается. [105] [106]
Фазово-контрастная рентгеновская визуализация (рис. 26) относится к различным методам, которые используют фазовую информацию когерентного рентгеновского пучка для получения изображений мягких тканей. (Для элементарного обсуждения см. Фазово-контрастная рентгеновская визуализация (введение) . Для более глубокого обзора см. Фазово-контрастная рентгеновская визуализация .) Она стала важным методом визуализации клеточных и гистологических структур в широком спектре биологических и медицинских исследований. Существует несколько технологий, используемых для рентгеновской фазово-контрастной визуализации, все из которых используют различные принципы для преобразования фазовых вариаций в рентгеновских лучах, исходящих от объекта, в вариации интенсивности. [107] [108] К ним относятся фазовый контраст на основе распространения, [109] интерферометрия Тальбота , [108] интерферометрия дальнего поля на основе муара , [110] визуализация с усилением рефракции, [111] и рентгеновская интерферометрия. [112] Эти методы обеспечивают более высокий контраст по сравнению с обычной рентгеновской визуализацией с поглощением-контрастом, что позволяет видеть более мелкие детали. Недостатком является то, что эти методы требуют более сложного оборудования, такого как синхротронные или микрофокусные рентгеновские источники, рентгеновская оптика или рентгеновские детекторы высокого разрешения.
Смотрите также
- Согласованность
- Когерентная сканирующая интерферометрия
- Датчик точного наведения (HST) (HST FGS — это интерферометры)
- Голография
- Интерферометрическая видимость
- Интерференционная литография
- Список типов интерферометров
- интерферометрия Рамсея
- Сейсмическая интерферометрия
- Принцип суперпозиции
- Интерферометрия со сверхдлинной базой
- Нулевой пространственный поток
Ссылки
- ^ Банч, Брайан Х.; Хеллеманс, Александр (апрель 2004 г.). История науки и техники . Houghton Mifflin Harcourt. стр. 695. ISBN 978-0-618-22123-3.
- ^ abcdefghijklmno Харихаран, П. (2007). Основы интерферометрии . Elsevier Inc. ISBN 978-0-12-373589-8.
- ^ Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2014). «Широкопольная двухлазерная интерферометрия». Optics Express . 22 (22): 27094–27101. Bibcode : 2014OExpr..2227094P. doi : 10.1364/OE.22.027094 . PMID 25401860.
- ↑ Т. Янг, «Бейкерианская лекция: эксперименты и расчеты, относящиеся к физической оптике», Философские труды Лондонского королевского общества 94 (1804): 1–16.
- ^ Кипнис, Наум (1991). История принципа интерференции света. doi :10.1007/978-3-0348-8652-9. ISBN 978-3-0348-9717-4.
- ^ Ж. Лекё, Франсуа Араго, французский гуманист XIX века и пионер астрофизики (Springer International Publishing: Выходные данные: Springer, 2015).
- ^ Нолти, Дэвид Д. (2023). Интерференция: история оптической интерферометрии и ученые, которые приручили свет (Oxford University Press, 2023). Oxford University Press. ISBN 978-0192869760.стр. 99-108
- ^ Нолти, Интерференция, стр.111
- ^ abcd Paschotta, Rüdiger. "Optical Heterodyne Detection". RP Photonics Consulting GmbH . Получено 1 апреля 2012 г.
- ^ Пул, Ян. "Супергетеродинный радиоприемник". Radio-Electronics.com . Получено 22 июня 2012 г.
- ^ Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2011). «Широкопольная гетеродинная интерферометрия с использованием пользовательской CMOS-камеры с модулированным светом». Optics Express . 19 (24): 24546–24556. Bibcode : 2011OExpr..1924546P. doi : 10.1364/OE.19.024546 . PMID 22109482.
- ^ Маллик, С.; Малакара, Д. (2007). "Common-Path Interferometers". Optical Shop Testing . стр. 97. doi :10.1002/9780470135976.ch3. ISBN 978-0-470-13597-6.
- ^ Верма, РК (2008). Волновая оптика. Discovery Publishing House. С. 97–110. ISBN 978-81-8356-114-3.
- ^ Колесниченко, Павел; Виттенбекер, Лукас; Зигмантас, Донатас (2020). «Полностью симметричный бездисперсионный стабильный пропускающий решетчатый интерферометр Майкельсона». Optics Express . 28 (25): 37752–37757. Bibcode : 2020OExpr..2837752K. doi : 10.1364/OE.409185 . PMID 33379604.
- ^ «Интерференционные устройства – Введение». OPI – Оптика для инженеров . Проверено 1 апреля 2012 г.
- ^ Ингрэм Тейлор, сэр Джеффри (1909). «Интерференционные полосы со слабым светом» (PDF) . Proc. Camb. Phil. Soc . 15 : 114. Получено 2 января 2013 г.
- ^ Йонссон, К. (1961). «Электронные помехи и лучшие художественные работы». Zeitschrift für Physik . 161 (4): 454–474. Бибкод : 1961ZPhy..161..454J. дои : 10.1007/BF01342460. S2CID 121659705.
- ^ Jönsson, C (1974). «Дифракция электронов на нескольких щелях». American Journal of Physics . 4 (1): 4–11. Bibcode : 1974AmJPh..42....4J. doi : 10.1119/1.1987592.
- ^ Arndt, M.; Zeilinger, A. (2004). "Неопределенность Гейзенберга и интерферометрия материальных волн с большими молекулами". В Buschhorn, GW; Wess, J. (ред.). Fundamental Physics – Heisenberg and Beyond: Werner Heisenberg Centennial Symposium "Developments in Modern Physics" . Springer. стр. 35–52. ISBN 978-3-540-20201-1.
- ^ Кэрролл, Бретт. "Simple Lloyd's Mirror" (PDF) . Американская ассоциация учителей физики . Получено 5 апреля 2012 г.
- ^ Serway, RA; Jewett, JW (2010). Принципы физики: текст, основанный на исчислении, том 1. Brooks Cole. стр. 905. ISBN 978-0-534-49143-7.
- ^ "Guideline for Use of Fizeau Interferometer in Optical Testing" (PDF) . NASA. Архивировано из оригинала (PDF) 25 сентября 2018 г. . Получено 8 апреля 2012 г. .
- ^ «Интерференционные устройства - Интерферометр Физо». Оптика для инженеров . Проверено 8 апреля 2012 г.
- ^ Zetie, KP; Adams, SF; Tocknell, RM "Как работает интерферометр Маха–Цендера?" (PDF) . Физический факультет, Вестминстерская школа, Лондон . Получено 8 апреля 2012 г. .
- ^ Ашкенас, Гарри И. (1950). Проектирование и строительство интерферометра Маха–Цендера для использования с трансзвуковой аэродинамической трубой GALCIT. Инженерная диссертация (англ.). Калифорнийский технологический институт. doi :10.7907/D0V1-MJ80.
- ^ Бетцлер, Клаус. «Интерферометр Фабри – Перо» (PDF) . Факберайх Физик, Университет Оснабрюка . Проверено 8 апреля 2012 г.
- ^ Нолти, Дэвид Д. (2012). Оптическая интерферометрия для биологии и медицины. Springer. стр. 17–26. Bibcode :2012oibm.book.....N. ISBN 978-1-4614-0889-5.
- ^ Майкельсон, AA; Морли, EW (1887). «Об относительном движении Земли и светоносного эфира» (PDF) . American Journal of Science . 34 (203): 333–345. Bibcode :1887AmJS...34..333M. doi :10.2475/ajs.s3-34.203.333. S2CID 124333204. Архивировано из оригинала (PDF) 2016-03-07 . Получено 2012-04-09 .
- ^ Miller, Dayton C. (1933). "Эксперимент по эфирному ветру и определение абсолютного движения Земли". Reviews of Modern Physics . 5 (3): 203–242. Bibcode :1933RvMP....5..203M. doi :10.1103/RevModPhys.5.203. S2CID 4119615.
Для наблюдений были выбраны полосы белого света, поскольку они состоят из небольшой группы полос, имеющих центральную, резко очерченную черную полосу, которая образует постоянную нулевую отметку для всех показаний.
- ^ Мюллер, Х.; Херрманн, С.; Браксмайер, К.; Шиллер, С.; Петерс, А. (2003). «Современный эксперимент Майкельсона–Морли с использованием криогенных оптических резонаторов». Phys. Rev. Lett . 91 (2): 020401. arXiv : physics/0305117 . Bibcode :2003PhRvL..91b0401M. doi :10.1103/PhysRevLett.91.020401. PMID 12906465. S2CID 15770750.
- ^ Eisele, C.; Nevsky, A.; Schiller, S. (2009). "Лабораторный тест изотропии распространения света на уровне 10-17". Physical Review Letters . 103 (9): 090401. Bibcode : 2009PhRvL.103i0401E. doi : 10.1103/PhysRevLett.103.090401. PMID 19792767. S2CID 33875626.
- ^ Herrmann, S.; Senger, A.; Möhle, K.; Nagel, M.; Kovalchuk, E.; Peters, A. (2009). "Эксперимент с вращающейся оптической полостью, проверяющий инвариантность Лоренца на уровне 10-17". Physical Review D. 80 ( 10): 105011. arXiv : 1002.1284 . Bibcode : 2009PhRvD..80j5011H. doi : 10.1103/PhysRevD.80.105011. S2CID 118346408.
- ^ Шеррер, PH; Богарт, RS; Буш, RI; Хоксема, J.; Косовичев, AG; Шоу, J. (1995). «Исследование солнечных колебаний – доплеровский тепловизор Майкельсона». Solar Physics . 162 (1–2): 129–188. Bibcode :1995SoPh..162..129S. doi :10.1007/BF00733429. S2CID 189848134.
- ^ Stroke, GW; Funkhouser, AT (1965). "Спектроскопия с преобразованием Фурье с использованием голографического изображения без вычислений и со стационарными интерферометрами" (PDF) . Physics Letters . 16 (3): 272–274. Bibcode :1965PhL....16..272S. doi :10.1016/0031-9163(65)90846-2. hdl : 2027.42/32013 . Получено 2 апреля 2012 г. .
- ^ Гэри, GA; Баласубраманиам, KS "Дополнительные заметки относительно выбора системы с несколькими эталонами для ATST" (PDF) . Advanced Technology Solar Telescope. Архивировано из оригинала (PDF) 10 августа 2010 г. Получено 29 апреля 2012 г.
- ^ «Спектрометрия с помощью преобразования Фурье». OPI – Оптика для инженеров . Проверено 3 апреля 2012 г.
- ^ "Солнечные бури Хэллоуина 2003: ультрафиолет SOHO/EIT, 195 Ã". NASA/Goddard Space Flight Center Scientific Visualization Studio. 2 апреля 2008 г. Архивировано из оригинала 23 апреля 2014 г. Получено 20 июня 2012 г.
- ^ "LIGO-Laser Interferometer Gravitational-Wave Observatory". Caltech/MIT . Получено 4 апреля 2012 г.
- ^ Кастельвекки, Давиде; Витце, Александра (11 февраля 2016 г.). «Наконец-то найдены гравитационные волны Эйнштейна». Nature News . doi :10.1038/nature.2016.19361. S2CID 182916902 . Получено 11 февраля 2016 г. .
- ^ Chevalerias, R.; Latron, Y.; Veret, C. (1957). «Методы интерферометрии, применяемые для визуализации потоков в аэродинамических трубах». Журнал оптического общества Америки . 47 (8): 703. Bibcode : 1957JOSA...47..703C. doi : 10.1364/JOSA.47.000703.
- ^ Ристич, Славица. "Методы визуализации потока в аэродинамических трубах – оптические методы (часть II)" (PDF) . Военно-технический институт, Сербия . Получено 6 апреля 2012 г. .
- ^ Париж, MGA (1999). «Запутанность и видимость на выходе интерферометра Маха–Цендера» (PDF) . Physical Review A . 59 (2): 1615–1621. arXiv : quant-ph/9811078 . Bibcode :1999PhRvA..59.1615P. doi :10.1103/PhysRevA.59.1615. S2CID 13963928. Архивировано из оригинала (PDF) 10 сентября 2016 г. . Получено 2 апреля 2012 г. .
- ^ Хаак, GR; Фёрстер, Х.; Бюттикер, М. (2010). «Обнаружение четности и запутывание с помощью интерферометра Маха–Цендера». Physical Review B. 82 ( 15): 155303. arXiv : 1005.3976 . Bibcode : 2010PhRvB..82o5303H. doi : 10.1103/PhysRevB.82.155303. S2CID 119261326.
- ^ ab Monnier, John D (2003). "Оптическая интерферометрия в астрономии" (PDF) . Reports on Progress in Physics . 66 (5): 789–857. arXiv : astro-ph/0307036 . Bibcode :2003RPPh...66..789M. doi :10.1088/0034-4885/66/5/203. hdl :2027.42/48845. S2CID 887574.
- ^ "Космическая калибровка". www.eso.org . Получено 10 октября 2016 г. .
- ^ Мальбет, Ф.; Керн, П.; Шанен-Дюпор, И.; Бергер, Ж.-П.; Руссле-Перро, К.; Бенек, П. (1999). «Интегральная оптика для астрономической интерферометрии». Астрон. Астрофиз. Доп. Сер . 138 : 135–145. arXiv : astro-ph/9907031 . Бибкод : 1999A&AS..138..135M. дои : 10.1051/аас: 1999496. S2CID 15342344.
- ^ Болдуин, Дж. Э.; Ханифф, К. А. (2002). «Применение интерферометрии к оптической астрономической визуализации». Phil. Trans. R. Soc. Lond. A. 360 ( 1794): 969–986. Bibcode : 2002RSPTA.360..969B. doi : 10.1098/rsta.2001.0977. PMID 12804289. S2CID 21317560.
- ^ Чжао, М.; Гис, Д.; Моннье, доктор медицинских наук; Тюро, Н.; Педретти, Э.; Барон, Ф.; Меранд, А.; Тен Бруммелаар, Т.; Макалистер, Х.; Риджуэй, Северная Каролина; Тернер, Н.; Штурманн Дж.; Штурманн, Л.; Фаррингтон, К.; Голдфингер, Пи Джей (2008). «Первые разрешенные изображения затменной и взаимодействующей двойной β-лиры». Астрофизический журнал . 684 (2): L95. arXiv : 0808.0932 . Бибкод : 2008ApJ...684L..95Z. дои : 10.1086/592146. S2CID 17510817.
- ^ Gerlich, S.; Eibenberger, S.; Tomandl, M.; Nimmrichter, S.; Hornberger, K.; Fagan, PJ; Tüxen, J.; Mayor, M.; Arndt, M. (2011). «Квантовая интерференция больших органических молекул». Nature Communications . 2 : 263–. Bibcode :2011NatCo...2..263G. doi :10.1038/ncomms1263. PMC 3104521 . PMID 21468015.
- ^ Хорнбергер, Клаус; Герлих, Стефан; Хаслингер, Филипп; Ниммрихтер, Стефан; Арндт, Маркус (8 февраля 2012 г.). «\textit{Коллоквиум}: Квантовая интерференция кластеров и молекул». Обзоры современной физики . 84 (1): 157–173. arXiv : 1109.5937 . Бибкод : 2012RvMP...84..157H. doi : 10.1103/RevModPhys.84.157. S2CID 55687641.
- ^ Эйбенбергер, Сандра; Герлих, Стефан; Арндт, Маркус; Майор, Марсель; Туксен, Йенс (14.08.2013). «Материйно-волновая интерференция частиц, выбранных из молекулярной библиотеки с массами, превышающими 10000 а.е.м.». Физическая химия Химическая физика . 15 (35): 14696–700. arXiv : 1310.8343 . Bibcode :2013PCCP...1514696E. doi :10.1039/C3CP51500A. ISSN 1463-9084. PMID 23900710. S2CID 3944699.
- ^ Lehmann, M; Lichte, H (декабрь 2002 г.). «Учебник по внеосевой электронной голографии». Microsc. Microanal . 8 (6): 447–66. Bibcode :2002MiMic...8..447L. doi :10.1017/S1431927602029938. PMID 12533207. S2CID 37980394.
- ^ Тономура, А. (1999). Электронная голография (2-е изд.). Springer. ISBN 978-3-540-64555-9.
- ^ Кляйн, Т. (2009). «Нейтронная интерферометрия: история трех континентов». Europhysics News . 40 (6): 24–26. Bibcode : 2009ENews..40f..24K. doi : 10.1051/epn/2009802 .
- ^ Димопулос, С.; Грэм, П. В.; Хоган, Дж. М.; Касевич, МА (2008). "Общие релятивистские эффекты в атомной интерферометрии". Phys. Rev. D. 78 ( 42003): 042003. arXiv : 0802.4098 . Bibcode : 2008PhRvD..78d2003D. doi : 10.1103/PhysRevD.78.042003. S2CID 119273854.
- ^ Mariani, Z.; Strong, K.; Wolff, M.; et al. (2012). «Инфракрасные измерения в Арктике с использованием двух интерферометров атмосферного излучения». Atmos. Meas. Tech . 5 (2): 329–344. Bibcode :2012AMT.....5..329M. doi : 10.5194/amt-5-329-2012 .
- ^ Мантравади, МВ; Малакара, Д. (2007). «Интерферометры Ньютона, Физо и Хайдингера». Тестирование оптического цеха . п. 1. дои : 10.1002/9780470135976.ch1. ISBN 978-0-470-13597-6.
- ^ Малакара, Д. (2007). «Интерферометр Тваймана – Грина». Тестирование оптического цеха . стр. 46–96. дои : 10.1002/9780470135976.ch2. ISBN 978-0-470-13597-6.
- ^ Майкельсон, А. А. (1918). «О коррекции оптических поверхностей». Труды Национальной академии наук Соединенных Штатов Америки . 4 (7): 210–212. Bibcode :1918PNAS....4..210M. doi : 10.1073/pnas.4.7.210 . PMC 1091444 . PMID 16576300.
- ^ «Интерференционные устройства - Интерферометр Тваймана-Грина» . OPI – Оптика для инженеров . Проверено 4 апреля 2012 г.
- ^ Хайдеман, РГ; Койман, РПХ; Греве, Дж. (1993). «Характеристики высокочувствительного оптического волноводного интерферометра Маха–Цендера иммуносенсора». Датчики и приводы B: Химия . 10 (3): 209–217. Bibcode :1993SeAcB..10..209H. CiteSeerX 10.1.1.556.5526 . doi :10.1016/0925-4005(93)87008-D.
- ^ Оливер, В. Д.; Ю, И.; Ли, Дж. К.; Берггрен, К. К.; Левитов, Л. С.; Орландо, TP (2005). «Интерферометрия Маха–Цендера в сильно управляемом сверхпроводящем кубите». Science . 310 (5754): 1653–1657. arXiv : cond-mat/0512691 . Bibcode :2005Sci...310.1653O. doi :10.1126/science.1119678. PMID 16282527. S2CID 46509116.
- ^ Nieradko, Ł.; Gorecki, C.; JóZwik, M.; Sabac, A.; Hoffmann, R.; Bertz, A. (2006). «Изготовление и оптическая упаковка интегрированного интерферометра Маха–Цендера поверх подвижного микрозеркала». Журнал микро/нанолитографии, MEMS и MOEMS . 5 (2): 023009. Bibcode : 2006JMM&M...5b3009N. doi : 10.1117/1.2203366.
- ^ Бердж, Дж. Х.; Чжао, К.; Дубин, М. (2010). "Измерение асферических зеркальных сегментов с использованием интерферометрии Физо с коррекцией CGH" (PDF) . Современные технологии в области космических и наземных телескопов и приборов . Том 7739. стр. 773902. Bibcode : 2010SPIE.7739E..02B. doi : 10.1117/12.857816. S2CID 49323922.
{{cite book}}:|journal=проигнорировано ( помощь ) - ^ Андерсон, Р.; Бильгер, ХР; Стедман, ГЭ (1994). ""Эффект Саньяка" Столетие интерферометров, вращающихся вокруг Земли" (PDF) . Am. J. Phys . 62 (11): 975–985. Bibcode :1994AmJPh..62..975A. doi :10.1119/1.17656 . Получено 30 марта 2012 г. .
- ^ Голио, Майк (2007). Радиочастотные и микроволновые приложения и системы. CRC Press. С. 14.1–14.17. ISBN 978-0-8493-7219-3. Получено 27 июня 2012 г.
- ^ Пашотта, Рюдигер. "Измерение ширины линии самогетеродина". RP Photonics . Получено 22 июня 2012 г.
- ^ "Optical Frequency Comb". Национальный исследовательский совет, Канада. Архивировано из оригинала 5 марта 2012 года . Получено 23 июня 2012 года .
- ^ Пашотта, Рюдигер. "Frequency Combs". RP Photonics . Получено 23 июня 2012 г.
- ^ Шмит, Дж. (1993). «Пространственные и временные методы измерения фазы: сравнение основных источников ошибок в одном измерении». В Brown, Gordon M.; Kwon, Osuk Y.; Kujawinska, Malgorzata; Reid, Graeme T. (ред.). Труды SPIE . Интерферометрия: методы и анализ. Том 1755. стр. 202–201. doi :10.1117/12.140770. S2CID 62679510.
- ^ Larkin, KG (1996). "Эффективный нелинейный алгоритм обнаружения огибающей в интерферометрии белого света" (PDF) . Журнал оптического общества Америки . 13 (4): 832–843. Bibcode :1996JOSAA..13..832L. CiteSeerX 10.1.1.190.4728 . doi :10.1364/JOSAA.13.000832. Архивировано из оригинала (PDF) 10 марта 2020 г. . Получено 1 апреля 2012 г. .
- ^ ISO. (2013). 25178-604:2013(E): Геометрическая спецификация изделия (GPS) – Текстура поверхности: Плоская – Номинальные характеристики бесконтактных (когерентная сканирующая интерферометрическая микроскопия) инструментов (ред. 2013(E)). Женева: Международная организация по стандартизации.
- ^ ab Harasaki, A.; Schmit, J.; Wyant, JC (2000). "Улучшенная вертикальная сканирующая интерферометрия" (PDF) . Applied Optics . 39 (13): 2107–2115. Bibcode :2000ApOpt..39.2107H. doi :10.1364/AO.39.002107. hdl : 10150/289148 . PMID 18345114. Архивировано из оригинала (PDF) 25 июля 2010 г. . Получено 21 мая 2012 г. .
- ^ Де Гроот, П (2015). «Принципы интерференционной микроскопии для измерения топографии поверхности». Advances in Optics and Photonics . 7 (1): 1–65. Bibcode :2015AdOP....7....1D. doi :10.1364/AOP.7.000001.
- ^ abc Olszak, AG; Schmit, J.; Heaton, MG "Interferometry: Technology and Applications" (PDF) . Bruker . Получено 1 апреля 2012 г. .
- ^ de Groot, Peter; Deck, Leslie (1995). "Профилирование поверхности с помощью анализа интерферограмм белого света в пространственной частотной области". Journal of Modern Optics . 42 (2): 389–401. Bibcode : 1995JMOp...42..389D. doi : 10.1080/09500349514550341.
- ^ ab "Фазово-сдвигающая интерферометрия для определения качества оптической поверхности". Newport Corporation. Архивировано из оригинала 7 ноября 2012 г. Получено 12 мая 2012 г.
- ^ ab "Как работают фазовые интерферометры". Graham Optical Systems. 2011. Получено 12 мая 2012 .
- ^ abc Шрайбер, Х.; Брюнинг, Дж. Х. (2007). "Интерферометрия со сдвигом фаз". Optical Shop Testing . стр. 547. doi :10.1002/9780470135976.ch14. ISBN 978-0-470-13597-6.
- ^ Соммаргрен, GE (1986). Патент США 4 594 003.
- ^ Ферраро, П.; Патурзо, М.; Грилли, С. (2007). «Измерение оптического волнового фронта с использованием нового фазосдвигающего точечного дифракционного интерферометра». SPIE . Получено 26 мая 2012 г.
- ^ P. de Groot, J., «Интерференционная микроскопия для анализа структуры поверхности», в Handbook of Optical Metrology, под редакцией T. Yoshizawa, гл. 31, стр. 791-828, (CRC Press, 2015).
- ^ Шмит, Дж.; Крит, К.; Вайант, Дж. К. (2007). «Профилировщики поверхности, многоволновая интерферометрия и интерферометрия белого света». Optical Shop Testing . стр. 667. doi :10.1002/9780470135976.ch15. ISBN 978-0-470-13597-6.
- ^ "HDVSI – Представляем высокоточную вертикальную сканирующую интерферометрию для исследований в области нанотехнологий от Veeco Instruments". Veeco. Архивировано из оригинала 9 апреля 2012 года . Получено 21 мая 2012 года .
- ^ Plucinski, J.; Hypszer, R.; Wierzba, P.; Strakowski, M.; Jedrzejewska-Szczerska, M.; Maciejewski, M.; Kosmowski, BB (2008). "Оптическая низкокогерентная интерферометрия для избранных технических приложений" (PDF) . Бюллетень Польской академии наук . 56 (2): 155–172 . Получено 8 апреля 2012 г. .
- ^ Yang, C.-H.; Wax, A; Dasari, RR; Feld, MS (2002). "2π-неоднозначное оптическое измерение расстояния с точностью до нанометра с помощью нового интерферометра с низкой когерентностью и пересечением фаз" (PDF) . Optics Letters . 27 (2): 77–79. Bibcode :2002OptL...27...77Y. doi :10.1364/OL.27.000077. PMID 18007717. S2CID 9524638.
- ^ Hitzenberger, CK; Sticker, M.; Leitgeb, R.; Fercher, AF (2001). «Дифференциальные фазовые измерения в низкокогерентной интерферометрии без неоднозначности 2pi». Optics Letters . 26 (23): 1864–1866. Bibcode : 2001OptL...26.1864H. doi : 10.1364/ol.26.001864. PMID 18059719.
- ^ Войтек Дж. Валецки, Кевин Лай, Виталий Сучков, Фук Ван, С.Х. Лау, Энн Ку Physica Status Solidi C Том 2, выпуск 3, страницы 984–989
- ^ WJ Walecki и др. «Бесконтактная быстрая метрология пластин для сверхтонких узорчатых пластин, установленных на шлифовальных и нарезных лентах» Симпозиум по технологиям производства электроники, 2004 г. IEEE/CPMT/SEMI 29-й Международный том, выпуск, 14–16 июля 2004 г. Страницы: 323–325
- ^ "Измерение толщины покрытия". Lumetrics, Inc. Архивировано из оригинала 29 октября 2013 г. Получено 28 октября 2013 г.
- ^ "Типичные измерения профилометрии". Novacam Technologies, Inc. Получено 25 июня 2012 г.
- ^ "Голографическая интерферометрия". Oquagen. 2008. Получено 22 мая 2012 .
- ^ Хехт, Джефф (1998). Лазер, свет миллиона применений. Dover Publications, Inc. стр. 229–230. ISBN 978-0-486-40193-5.
- ^ abc Fein, H (сентябрь 1997). "Голографическая интерферометрия: неразрушающий инструмент" (PDF) . The Industrial Physicist : 37–39. Архивировано из оригинала (PDF) 2012-11-07.
- ^ "PIA01762: Космическое радиолокационное изображение Килауэа, Гавайи". NASA/JPL. 1999. Получено 17 июня 2012 .
- ^ Джонс Р. и Уайкс К., Голографическая и спекл-интерферометрия, 1989, Cambridge University Press
- ^ Баттерс, Дж. Н.; Линдерц, Дж. А. (1971). «Метод двойной экспозиции для интерферометрии спекл-структур». Журнал физики E: Научные приборы . 4 (4): 277–279. Bibcode : 1971JPhE....4..277B. doi : 10.1088/0022-3735/4/4/004.
- ^ Дворжакова, П.; Байгар, В.; Трнка, Й. (2007). «Динамическая электронная спекл-интерферометрия в применении для измерения смещения вне плоскости» (PDF) . Инженерная механика . 14 (1/2): 37–44.
- ^ Moustafa, NA; Hendawi, N. (2003). "Comparative Phase-Shifting Digital Speckle Pattern Interferometry Using Single Reference Beam Technique" (PDF) . Egypt. J. Sol . 26 (2): 225–229. doi : 10.21608/ejs.2003.150160 . Получено 22 мая 2012 .
- ^ Буга, А.; Йокела, Я.; Путримас, Р. «Прослеживаемость, стабильность и использование базовой линии калибровки Кивишкес–первые 10 лет» (PDF) . Экологическая инженерия, 7-я международная конференция . Вильнюсский технический университет имени Гедиминаса. С. 1274–1280 . Получено 9 апреля 2012 г. .
- ^ Нолти, Дэвид Д. (2012). Оптическая интерферометрия для биологии и медицины . Springer. Bibcode :2012oibm.book.....N. ISBN 978-1-4614-0889-5.
- ^ Хуан, Д.; Свансон, EA; Линь, CP; Шуман, JS; Стинсон, WG; Чанг, W.; Хи, MR; Флотт, T.; Грегори, K.; Пулиафито, CA; Фудзимото, JG (1991). "Оптическая когерентная томография" (PDF) . Наука . 254 (5035): 1178–81. Bibcode :1991Sci...254.1178H. doi :10.1126/science.1957169. PMC 4638169 . PMID 1957169 . Получено 10 апреля 2012 г. .
- ^ Fercher, AF (1996). "Оптическая когерентная томография" (PDF) . Журнал биомедицинской оптики . 1 (2): 157–173. Bibcode :1996JBO.....1..157F. doi :10.1117/12.231361. PMID 23014682. Архивировано из оригинала (PDF) 25 сентября 2018 г. . Получено 10 апреля 2012 г. .
- ^ Лэнг, Уолтер. «Дифференциальная интерференционно-контрастная микроскопия Номарского» (PDF) . Карл Цейсс, Оберкохен . Проверено 10 апреля 2012 г.
- ^ Wax, A.; Pyhtila, JW; Graf, RN; Nines, R.; Boone, CW; Dasari, RR; Feld, MS; Steele, VE; Stoner, GD (2005). "Проспективная градация неопластических изменений в эпителии пищевода крыс с использованием интерферометрии с низким разрешением по углу". Журнал биомедицинской оптики . 10 (5): 051604. Bibcode : 2005JBO....10e1604W. doi : 10.1117/1.2102767. hdl : 1721.1/87657 . PMID 16292952.
- ^ Pyhtila, JW; Chalut, KJ; Boyer, JD; Keener, J.; d'Amico, T.; Gottfried, M.; Gress, F.; Wax, A. (2007). «In situ обнаружение ядерной атипии в пищеводе Барретта с использованием низкокогерентной интерферометрии с угловым разрешением». Гастроинтестинальная эндоскопия . 65 (3): 487–491. doi :10.1016/j.gie.2006.10.016. PMID 17321252.
- ^ Фицджеральд, Ричард (2000). «Фазочувствительная рентгеновская визуализация». Physics Today . 53 (7): 23–26. Bibcode : 2000PhT....53g..23F. doi : 10.1063/1.1292471 . S2CID 121322301.
- ^ ab Дэвид, C; Нохаммер, B; Солак, HH и Циглер E (2002). «Дифференциальная рентгеновская фазово-контрастная визуализация с использованием сдвигового интерферометра». Applied Physics Letters . 81 (17): 3287–3289. Bibcode : 2002ApPhL..81.3287D. doi : 10.1063/1.1516611 .
- ^ Уилкинс, SW; Гуреев, TE; Гао, D; Погани, A и Стивенсон, AW (1996). «Фазово-контрастная визуализация с использованием полихроматических жестких рентгеновских лучей». Nature . 384 (6607): 335–338. Bibcode :1996Natur.384..335W. doi :10.1038/384335a0. S2CID 4273199.
- ^ Miao, Houxun; Panna, Alireza; Gomella, Andrew A.; Bennett, Eric E.; Znati, Sami; Chen, Lei; Wen, Han (2016). «Универсальный эффект муара и его применение в рентгеновской фазово-контрастной визуализации». Nature Physics . 12 (9): 830–834. Bibcode :2016NatPh..12..830M. doi :10.1038/nphys3734. PMC 5063246 . PMID 27746823.
- ^ Дэвис, Т.Дж.; Гао, Д.; Гуреев, ТЕ; Стивенсон, А.В. и Уилкинс, С.В. (1995). «Фазово-контрастная визуализация слабо поглощающих материалов с использованием жестких рентгеновских лучей». Nature . 373 (6515): 595–598. Bibcode :1995Natur.373..595D. doi :10.1038/373595a0. S2CID 4287341.
- ^ Момосе, А.; Такеда, Т.; Итай, И. и Хирано, К. (1996). «Фазовоконтрастная рентгеновская компьютерная томография для наблюдения за биологическими мягкими тканями». Nature Medicine . 2 (4): 473–475. doi :10.1038/nm0496-473. PMID 8597962. S2CID 23523144.









