Гидравлический прыжок

Гидравлический прыжок — это явление в науке гидравлики , которое часто наблюдается в открытых русловых потоках , таких как реки и водосбросы . Когда жидкость с высокой скоростью выливается в зону с более низкой скоростью, на поверхности жидкости происходит довольно резкий подъем. Быстро текущая жидкость резко замедляется и увеличивается в высоте, преобразуя часть первоначальной кинетической энергии потока в увеличение потенциальной энергии, при этом часть энергии необратимо теряется из-за турбулентности в тепло. В открытом русле потока это проявляется в том, что быстрый поток быстро замедляется и нагромождается сам на себя, подобно тому, как образуется ударная волна .
Впервые это явление наблюдал и задокументировал Леонардо да Винчи в 1500-х годах. [1] Математика была впервые описана Джорджо Бидоне из Туринского университета , когда он опубликовал в 1820 году статью под названием « Опыты на удалении и распространении волн» . [2]
Это явление зависит от начальной скорости жидкости. Если начальная скорость жидкости ниже критической скорости, то скачок невозможен. Для начальных скоростей потока, которые не намного превышают критическую скорость , переход выглядит как волнообразная волна. По мере дальнейшего увеличения начальной скорости потока переход становится более резким, пока при достаточно высоких скоростях фронт перехода не сломается и не закрутится обратно на себя. Когда это происходит, скачок может сопровождаться сильной турбулентностью, завихрением, вовлечением воздуха и поверхностными волнами или волнами .
Существует два основных проявления гидравлических прыжков, и для каждого из них исторически использовалась разная терминология. Однако механизмы, лежащие в их основе, схожи, поскольку они являются просто вариациями друг друга, рассматриваемыми с разных систем отсчета, и поэтому физика и методы анализа могут использоваться для обоих типов.
Различные проявления:
- Стационарный гидравлический прыжок – быстро текущая вода переходит в стационарный прыжок в медленно движущуюся воду, как показано на рисунках 1 и 2.
- Приливная волна — стена или волнообразная волна воды, движущаяся вверх по течению против течения воды, текущей вниз по течению, как показано на рисунках 3 и 4. Если рассмотреть систему отсчета, которая движется вместе с фронтом волны, то фронт волны неподвижен относительно системы и имеет то же самое существенное поведение, что и стационарный скачок.
Схожий случай — каскад: стена или волнообразная волна воды движется вниз по течению, обгоняя более мелкий поток воды, расположенный ниже по течению, как показано на рисунке 5. Если рассматривать это из системы отсчета, которая движется вместе с фронтом волны, это поддается такому же анализу, что и стационарный прыжок.

Эти явления рассматриваются в обширной литературе с различных технических точек зрения. [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13 ] [14] [ 15] [16] [17] [18]
Гидравлический прыжок иногда используется при смешивании химикатов. [19]
Занятия гидравлическими прыжками

Гидравлические прыжки можно наблюдать как в стационарной форме, которая известна как «гидравлический прыжок», так и в динамической или подвижной форме, которая известна как положительный всплеск или «гидравлический прыжок в трансляции». [16] Их можно описать с помощью тех же аналитических подходов, и они являются просто вариантами одного явления. [15] [16] [18]
Движущийся гидравлический прыжок

Приливная волна — это гидравлический скачок, который происходит, когда прилив образует волну (или волны) воды, которая движется вверх по реке или узкому заливу против направления течения. [16] Как и в случае гидравлических скачков в целом, волны принимают различные формы в зависимости от разницы в уровне воды вверх и вниз по течению, от волнообразного волнового фронта до ударно-волнообразной стены воды. [9] На рисунке 3 показана приливная волна с характеристиками, общими для мелководной воды вверх по течению — наблюдается большая разница высот. На рисунке 4 показана приливная волна с характеристиками, общими для глубокой воды вверх по течению — наблюдается небольшая разница высот, а фронт волны волнообразен. В обоих случаях приливная волна движется со скоростью, характерной для волн в воде глубины, находящейся непосредственно за фронтом волны. Ключевой особенностью приливных волн и положительных нагонов является интенсивное турбулентное перемешивание, вызванное прохождением фронта волны и последующим движением волны. [20]

Другой вариант движущегося гидравлического прыжка — каскад. В каскаде серия катящихся волн или волнообразных волн воды движется вниз по течению, обгоняя более мелкий поток воды, находящийся ниже по течению.
Движущийся гидравлический прыжок называется нагон. В случае положительных нагонов движение волны происходит быстрее в верхней части, чем в нижней.
Стационарный гидравлический прыжок
Стационарный гидравлический прыжок — это тип, который чаще всего наблюдается на реках и на инженерных сооружениях, таких как водосбросы плотин и ирригационные сооружения. Они возникают, когда поток жидкости с высокой скоростью попадает в зону реки или инженерного сооружения, которая может поддерживать только более низкую скорость. Когда это происходит, вода замедляется в довольно резком подъеме (ступенька или стоячая волна ) на поверхности жидкости. [17]
Сравнивая характеристики до и после, можно обнаружить:
| Характеристика | Перед прыжком | После прыжка |
|---|---|---|
| скорость жидкости | сверхкритический (быстрее скорости волны), также известный как выстрел или сверхзвуковой | субкритический, также известный как спокойный или субундальный |
| высота жидкости | низкий | высокий |
| поток | обычно гладкий турбулентный | обычно турбулентный поток (бурный и прерывистый) |
Другой стационарный гидравлический прыжок происходит, когда быстрый поток встречает подводный объект, который выбрасывает воду вверх. Математика, лежащая в основе этой формы, более сложная и должна учитывать форму объекта и характеристики потока жидкости вокруг него.
Анализ гидравлического прыжка на поверхности жидкости

Несмотря на кажущуюся сложность перехода потока, применение простых аналитических инструментов к двумерному анализу эффективно для получения аналитических результатов, которые тесно связаны как с полевыми, так и с лабораторными результатами. Анализ показывает:
- Высота прыжка: соотношение между глубиной до и после прыжка как функция скорости потока [18]
- Потеря энергии при прыжке
- Место прыжка на естественной или искусственной поверхности
- Характер прыжка: волнообразный или резкий.
Высота прыжка
Высота прыжка определяется применением уравнений сохранения массы и импульса. [18] Существует несколько методов прогнозирования высоты гидравлического прыжка. [3] [4] [5] [6] [10] [15] [18] [21]
Все они приходят к общим выводам:
- Соотношение глубины воды до и после прыжка зависит исключительно от отношения скорости воды, поступающей в трамплин, к скорости волны, набегающей на движущуюся воду.
- Высота прыжка может во много раз превышать начальную глубину воды.
Для известного расхода, как показано на рисунке ниже, приближение, что поток импульса одинаков только вверх и вниз по течению принципа энергии, дает выражение потери энергии в гидравлическом прыжке. Гидравлические прыжки обычно используются в качестве гасителей энергии ниже по течению от водосбросов плотин.

- Применение принципа непрерывности
В гидродинамике уравнение непрерывности фактически является уравнением сохранения массы . Рассматривая любую фиксированную замкнутую поверхность внутри несжимаемой движущейся жидкости, жидкость втекает в заданный объем в некоторых точках и вытекает в других точках вдоль поверхности без чистого изменения массы в пространстве, поскольку плотность постоянна. В случае прямоугольного канала равенство потока массы вверх по течению ( ) и вниз по течению ( ) дает:
- или
с плотностью жидкости и усредненными по глубине скоростями потока вверх и вниз по течению, а также соответствующими глубинами воды.
- Сохранение потока импульса
Для прямого призматического прямоугольного канала сохранение потока импульса через прыжок, предполагая постоянную плотность, можно выразить как:
В прямоугольном канале такое уравнение сохранения можно дополнительно упростить до безразмерной формы уравнения My , которая широко используется в гидравлическом анализе прыжков в открытом канале.
Высота прыжка в терминах потока. Деление на константу и введение результата из непрерывности дает
что после некоторой алгебры упрощается до:
где Здесь — безразмерное число Фруда , связывающее инерционные и гравитационные силы в восходящем потоке. Решение этого квадратного уравнения дает:
Отрицательные ответы не дают значимых физических решений, поэтому это сводится к:
- так
известное как уравнение Беланже . Результат может быть распространен на нерегулярное поперечное сечение. [18]

Это дает три класса решений:
- Когда , то (т.е. скачка нет)
- Когда , то (т.е. имеет место отрицательный скачок – это можно показать как несохранение энергии и физически возможно только в том случае, если некоторая сила ускорит жидкость в этой точке)
- Когда , то (т.е. имеет место положительный скачок)
Это эквивалентно условию, что . Поскольку — скорость мелкой гравитационной волны , условие эквивалентно утверждению, что начальная скорость представляет собой сверхкритический поток (число Фруда > 1), а конечная скорость представляет собой докритический поток (число Фруда < 1).
- Волнистость ниже по течению от прыжка
На практике это означает, что вода, ускоренная крупными каплями, может создавать более сильные стоячие волны ( волнистые боры ) в виде гидравлических прыжков, поскольку она замедляется у основания капли. Такие стоячие волны, обнаруженные ниже по течению от плотины или естественного скального уступа, могут образовывать чрезвычайно опасный «хранитель» с водяной стеной, которая «удерживает» плавающие объекты (например, бревна, байдарки или байдарочников) рециркулирующими в стоячей волне в течение длительных периодов времени.
Рассеивание энергии посредством гидравлического прыжка

Одним из важнейших инженерных применений гидравлического прыжка является рассеивание энергии в каналах, водосбросах плотин и подобных сооружениях, чтобы избыточная кинетическая энергия не повредила эти сооружения. Скорость рассеивания энергии или потери напора через гидравлический прыжок является функцией числа Фруда притока гидравлического прыжка и высоты прыжка. [15]
Потеря энергии при гидравлическом прыжке, выраженная как потеря напора, составляет:
[22]
Расположение гидравлического прыжка в русле реки или инженерном сооружении
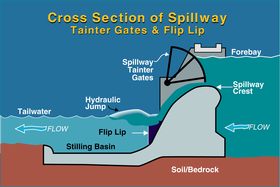
При проектировании плотины энергия быстротекущего потока через водосброс должна быть частично рассеяна, чтобы предотвратить эрозию русла реки ниже водосброса, что в конечном итоге может привести к разрушению плотины. Это можно сделать, организовав образование гидравлического прыжка для рассеивания энергии. Чтобы ограничить ущерб, этот гидравлический прыжок обычно происходит на фартуке, спроектированном так, чтобы выдерживать гидравлические силы и предотвращать локальную кавитацию и другие явления, которые ускоряют эрозию.
При проектировании водосброса и фартука инженеры выбирают точку, в которой произойдет гидравлический прыжок. Препятствия или изменения уклона обычно проектируются в фартуке, чтобы вызвать прыжок в определенном месте. Препятствия не нужны, так как обычно достаточно одного изменения уклона. Чтобы вызвать гидравлический прыжок без препятствий, фартук проектируется таким образом, что плоский уклон фартука задерживает быстро текущую воду из водосброса. Если уклон фартука недостаточен для поддержания изначально высокой скорости, произойдет прыжок.

Распространены два метода проектирования индуцированного прыжка:
- Если поток воды вниз по течению ограничен каналом вниз по течению таким образом, что вода возвращается к основанию водосброса, то этот уровень воды вниз по течению можно использовать для определения места прыжка.
- Если водосброс продолжает опускаться на некоторое расстояние, но уклон изменяется таким образом, что он больше не может поддерживать сверхкритический поток, то глубина в нижней области докритического потока достаточна для определения места прыжка.
В обоих случаях конечная глубина воды определяется характеристиками нижнего течения. Скачок произойдет тогда и только тогда, когда уровень втекающей (сверхкритической) воды ( ) удовлетворяет условию:
- = Число Фруда вверх по течению
- g = ускорение свободного падения (в данном случае практически постоянное)
- h = высота жидкости ( = начальная высота, в то время как = высота вверх по течению)
Вовлечение воздуха в гидравлические прыжки
Гидравлический прыжок характеризуется высокотурбулентным потоком. Макромасштабные вихри развиваются в ролике прыжка и взаимодействуют со свободной поверхностью, что приводит к захвату пузырьков воздуха, образованию брызг и капель в области двухфазного потока. [23] [24] Воздушно-водяной поток связан с турбулентностью, которая также может приводить к переносу осадка. Турбулентность может сильно зависеть от динамики пузырьков. Физически механизмы, вовлеченные в эти процессы, сложны.
Вовлечение воздуха происходит в форме пузырьков воздуха и воздушных пакетов, захваченных при столкновении восходящего струйного потока с роликом. Воздушные пакеты разбиваются на очень маленькие пузырьки воздуха, поскольку они вовлекаются в область сдвига, характеризующуюся большим содержанием воздуха и максимальным количеством пузырьков. [25] После того, как вовлекаемые пузырьки адвектируются в области меньшего сдвига, столкновения пузырьков и коалесценция приводят к более крупным воздушным образованиям, которые перемещаются к свободной поверхности за счет комбинации плавучести и турбулентной адвекции.
Табличное резюме аналитических выводов
| Величина потока вверх по течению является сверхкритической (т.е. предпрыжковое число Фруда) | Соотношение высоты после прыжка к высоте до прыжка | Описательная характеристика прыжка | Доля энергии, рассеиваемая при прыжке [11] |
|---|---|---|---|
| ≤ 1,0 | 1.0 | Скачка нет; для возникновения скачка поток должен быть сверхкритическим | никто |
| 1,0–1,7 | 1,0–2,0 | Стоячая или волнообразная волна | < 5% |
| 1,7–2,5 | 2,0–3,1 | Слабый прыжок (серия небольших роликов) | 5% – 15% |
| 2,5–4,5 | 3.1–5.9 | Колеблющийся прыжок | 15% – 45% |
| 4,5–9,0 | 5,9–12,0 | Стабильный, четко выраженный, хорошо сбалансированный прыжок | 45% – 70% |
| > 9.0 | > 12.0 | Четко выраженный, турбулентный, сильный прыжок | 70% – 85% |
Примечание: приведенная выше классификация очень грубая. Волнообразные гидравлические скачки наблюдались при числах Фруда до притока/предскачка до 3,5–4. [15] [16]
Гидравлические вариации прыжков
Аналогичному анализу поддаются ряд вариаций:
Неглубокие гидравлические прыжки жидкости
- Гидравлический прыжок в раковину
Рисунок 2 выше иллюстрирует пример гидравлического прыжка, часто наблюдаемого в кухонной раковине. Вокруг места, где водопроводная вода попадает в раковину, будет наблюдаться плавный поток. Чуть дальше будет наблюдаться внезапный «скачок» уровня воды. Это гидравлический прыжок.
Круговая падающая струя создает тонкую пленку жидкости, которая распространяется радиально, с круговым гидравлическим скачком, происходящим ниже по течению. Для ламинарных струй тонкая пленка и гидравлический скачок могут быть на удивление гладкими и устойчивыми. В 1993 году Лю и Линхард продемонстрировали роль поверхностного натяжения в установлении структуры гидравлических скачков в этих тонких пленках. [26] Во многих последующих исследованиях изучалось поверхностное натяжение и формирование узора такими скачками. [27]
Исследование 2018 года [28] экспериментально и теоретически исследовало относительный вклад поверхностного натяжения и силы тяжести в круговой гидравлический прыжок. Чтобы исключить роль силы тяжести в формировании кругового гидравлического прыжка, авторы провели эксперименты на горизонтальных, вертикальных и наклонных поверхностях, обнаружив, что независимо от ориентации подложки, при одинаковой скорости потока и физических свойствах жидкости начальный гидравлический прыжок происходит в одном и том же месте. Они предложили модель для этого явления и обнаружили, что общим критерием для тонкопленочного гидравлического прыжка является
где — локальное число Вебера , а — локальное число Фруда . Для гидравлических прыжков накипи на кухонной раковине число Фруда остается высоким, поэтому эффективным критерием для гидравлического прыжка тонкой пленки является . Другими словами, гидравлический прыжок тонкой пленки происходит, когда импульс жидкости на единицу ширины равен поверхностному натяжению жидкости. [28] Однако эта модель остается весьма спорной. [29]
Внутренние волновые гидравлические прыжки
Гидравлические прыжки в абиссальном конусе выноса
Мутностные потоки могут приводить к внутренним гидравлическим скачкам (т. е. гидравлическим скачкам как внутренним волнам в жидкостях различной плотности) при формировании абиссальных конусов выноса . Внутренние гидравлические скачки связаны с стратификацией, вызванной соленостью или температурой , а также с разницей в плотности из-за взвешенных материалов. Когда наклон ложа (по которому течет мутностный поток) становится плоским, более медленная скорость потока отражается в увеличенном отложении осадков под потоком, создавая постепенный обратный уклон. Там, где происходит гидравлический скачок, сигнатура представляет собой резкий обратный уклон, соответствующий быстрому снижению скорости потока в точке скачка. [30]
Атмосферные гидравлические прыжки
Гидравлические прыжки происходят в атмосфере в воздухе, протекающем над горами. [31] Гидравлический прыжок также происходит на границе тропопаузы между стратосферой и тропосферой по ветру от пролетающей вершины очень сильных сверхъячеечных гроз. [32] Схожая ситуация — облако Morning Glory , наблюдаемое, например, в Северной Австралии, иногда называемое волновым прыжком. [16]
Промышленное и рекреационное применение гидравлических прыжков
Промышленный
Гидравлический прыжок является наиболее часто используемым выбором инженеров-проектировщиков для рассеивания энергии ниже водосбросов и водовыпусков. Правильно спроектированный гидравлический прыжок может обеспечить 60-70% рассеивания энергии в самом бассейне, ограничивая ущерб сооружениям и руслу реки. Даже при таком эффективном рассеивании энергии успокоительные бассейны должны быть тщательно спроектированы, чтобы избежать серьезных повреждений из-за подъема, вибрации, кавитации и истирания. Для этого типа проектирования была разработана обширная литература. [7] [8] [13] [15]

Рекреационный
Во время путешествия по реке гребцы на байдарках и каноэ часто останавливаются и играют на стоячих волнах и гидравлических трамплинах. Стоячие волны и ударные фронты гидравлических трамплинов делают такие места популярными для такого отдыха.
Аналогичным образом, каякеры и серферы, как известно, преодолевают приливные волны вверх по рекам.
Гидравлические прыжки использовались пилотами планеров в Андах и Альпах [31], а также для катания на эффектах Morning Glory в Австралии. [33]
Смотрите также
- Ламинарный поток – поток, в котором частицы жидкости следуют по плавным траекториям в слоях.
- Ударная волна – Распространяющееся возмущение
- Приливная волна — водная волна, движущаяся вверх по течению реки или узкого залива из-за набегающего прилива.
- Турбулентность – движение, характеризующееся хаотическими изменениями давления и скорости потока.
- Волновой бор – волновое возмущение в атмосфере Земли, которое можно увидеть через уникальные облачные образования.
Ссылки и примечания
- ^ "Бытовой феномен, наблюдаемый Леонардо да Винчи, наконец-то объяснен" . Получено 2018-08-08 .
- ^ Кабрера, Энрике (2010). Водное хозяйство и управление во времени: извлечение уроков из истории . CRC Press. ISBN 978-0415480024.
- ^ ab Douglas, JF; Gasiorek, JM; Swaffield, JA (2001). Механика жидкостей (4-е изд.). Эссекс: Prentice Hall. ISBN 978-0-582-41476-1.
- ^ ab Faber, TE (1995). Динамика жидкости для физиков . Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-42969-6.
- ^ ab Faulkner, LL (2000). Практическая механика жидкости для инженерных приложений . Базиль, Швейцария: Marcel Dekker AG. ISBN 978-0-8247-9575-7.
- ^ ab Fox, RW; McDonald, AT (1985). Введение в механику жидкости . John Wiley & Sons. ISBN 978-0-471-88598-6.
- ^ abcd Хагер, Вилли Х. (1995). Рассеиватели энергии и гидравлический прыжок . Дордрехт: Kluwer Academic Publishers. ISBN 978-90-5410-198-7.
- ^ abcd Хацурия, Р. М. (2005). Гидравлика водосбросов и гасителей энергии . Нью-Йорк: Марсель Деккер. ISBN 978-0-8247-5789-2.
- ^ ab Lighthill, James (1978). Волны в жидкостях . Кембридж: Cambridge University Press. ISBN 978-0-521-29233-7.
- ^ ab Roberson, JA; Crowe, CT (1990). Инженерная механика жидкостей . Бостон: Houghton Mifflin Company. ISBN 978-0-395-38124-3.
- ^ ab Streeter, VL; Wylie, EB (1979). Механика жидкостей . Нью-Йорк: McGraw-Hill Book Company. ISBN 978-0-07-062232-6.
- ^ Веннард, Джон К. (1963). Элементарная механика жидкости (4-е изд.). Нью-Йорк: John Wiley & Sons.
- ^ abcd Вишер, DL; Хагер, WH (1995). Рассеиватели энергии . Роттердам: А.А. Балкема. ISBN 978-0-8247-5789-2.
- ^ Уайт, Фрэнк М. (1986). Механика жидкости . McGraw Hill, Inc. ISBN 978-0-07-069673-0.
- ^ abcdefgh Шансон, Х. (2004). Гидравлика потока в открытом канале: введение (2-е изд.). Баттерворт-Хайнеманн. ISBN 978-0-7506-5978-9.
- ^ abcdef Chanson, H. (2009). «Современные знания в области гидравлических прыжков и связанных с ними явлений. Обзор экспериментальных результатов» (PDF) . European Journal of Mechanics B. 28 ( 2): 191– 210. Bibcode : 2009EuJMB..28..191C. doi : 10.1016/j.euromechflu.2008.06.004.
- ^ ab Murzyn, F.; Chanson, H. (2009). «Свободные поверхностные флуктуации при гидравлических скачках: экспериментальные наблюдения». Experimental Thermal and Fluid Science . 33 (7): 1055– 1064. Bibcode :2009ETFS...33.1055M. doi :10.1016/j.expthermflusci.2009.06.003.
- ^ abcdef Шансон, Хьюберт (апрель 2012 г.). «Учет импульса в гидравлических прыжках и скважинах» (PDF) . Журнал по ирригации и дренажной технике . 138 (4): 382– 385. doi :10.1061/(ASCE)IR.1943-4774.0000409.
- ^ "Гидравлический прыжок - Типы и характеристики гидравлического прыжка". The Constructor . 2016-06-17 . Получено 2019-12-26 .
- ^ Кох, К.; Шансон, Х. (2009). «Измерения турбулентности в положительных нагонах и скважинах» (PDF) . Журнал гидравлических исследований . 47 (1): 29– 40. Bibcode : 2009JHydR..47...29K. doi : 10.3826/jhr.2009.2954. S2CID 124743367.
- ^ В этом разделе подходы излагаются только на обзорном уровне.
- ^ "Потери энергии при гидравлическом прыжке". sdsu. Архивировано из оригинала 17 июля 2007 г. Получено 1 июля 2015 г.
- ^ Чансон, Х.; Браттберг, Т. (2000). «Экспериментальное исследование сдвигового потока воздух-вода в гидравлическом прыжке» (PDF) . Международный журнал многофазного потока . 26 (4): 583– 607. Bibcode : 2000IJMF...26..583C. doi : 10.1016/S0301-9322(99)00016-6.
- ^ Murzyn, F.; Chanson, H. (2009). «Свойства двухфазного потока газа и жидкости в гидравлическом прыжке: обзор и перспективы». В S. Martin и JR Williams (ред.). Исследование многофазного потока (PDF) . Hauppauge NY, USA: Nova Science Publishers. Глава 9, стр. 497–542. ISBN 978-1-60692-448-8.
- ^ Chanson, H. (2007). "Структура пузырькового потока в гидравлическом прыжке" (PDF) . European Journal of Mechanics B. 26 ( 3): 367– 384. Bibcode : 2007EuJMB..26..367C. doi : 10.1016/j.euromechflu.2006.08.001.
- ^ Лю, Синь; Лиенхард, Джон Х. (июль 1993 г.). «Гидравлический скачок при соударении круглых струй и в других тонких жидких пленках». Эксперименты по жидкостям . 15 (2): 108– 116. Bibcode : 1993ExFl...15..108L. doi : 10.1007/BF00190950.
- ^ Буш, Джон ВМ; Аристофф, Джеффри М. (2003). «Влияние поверхностного натяжения на круговой гидравлический прыжок». Журнал механики жидкости . 489 : 229–238 . Bibcode : 2003JFM...489..229B. doi : 10.1017/S0022112003005159.
- ^ ab Bhagat, RK; Jha, NK; Linden, PF; Wilson, DI (2018). «О происхождении кругового гидравлического прыжка в тонкой жидкой пленке». Journal of Fluid Mechanics . 851 : R5. arXiv : 1712.04255 . Bibcode :2018JFM...851R...5B. doi :10.1017/jfm.2018.558. S2CID 119515628.
- ^ Дюшен, Алексис; Лимат, Лоран (28.02.2022). «Круговые гидравлические прыжки: где имеет значение поверхностное натяжение?». Журнал механики жидкости . 937. arXiv : 2112.09538 . Bibcode : 2022JFM...937R...2D. doi : 10.1017/jfm.2022.136. ISSN 0022-1120 . S2CID 245329387.
- ^ Костич, Светлана; Паркер, Гэри (2006). «Реакция мутных течений на переход каньон-конус выноса: внутренние гидравлические скачки и осадочные признаки». Журнал гидравлических исследований . 44 (5): 631– 653. Bibcode : 2006JHydR..44..631K. doi : 10.1080/00221686.2006.9521713. S2CID 53700725.
- ^ ab Клеман, Жан Мари (2015). Танцы с ветром . Pivetta Partners. ISBN 978-8890343247.
- ^ «Динамика гидравлического прыжка над грозами сверхъячейки», Science, O'Neill et al, Vol. 373, Issue 6560, 10 сентября 2021 г.
- ^ "Облачные серферы катаются на Утренней глории на севере Квинсленда". ABC News . 3 октября 2017 г. Получено 12 июня 2018 г.
Дальнейшее чтение
- Шансон, Хьюберт (2009). «Современные знания в области гидравлических прыжков и связанных с ними явлений. Обзор экспериментальных результатов» (PDF) . European Journal of Mechanics B. 28 ( 2): 191– 210. Bibcode : 2009EuJMB..28..191C. doi : 10.1016/j.euromechflu.2008.06.004.






























