Шестиугольная решетка
 |  | 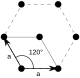 |
| Шестиугольная решетка | Группа обоев p6m | Элементарная ячейка |
|---|
Шестиугольная решетка (иногда называемая треугольной решеткой ) является одним из пяти типов двумерной решетки Браве . [1] Категория симметрии решетки — группа обоев p6m. Векторы примитивного переноса шестиугольной решетки образуют угол 120° и имеют одинаковую длину,
Обратная решетка гексагональной решетки представляет собой гексагональную решетку в обратном пространстве с ориентацией, измененной на 90°, и примитивными векторами решетки длиной
Набор точек сот

Множество точек сот является частным случаем гексагональной решетки с двухатомным базисом. [1] Центры шестиугольников сот образуют гексагональную решетку, а множество точек сот можно рассматривать как объединение двух смещенных гексагональных решеток.
В природе атомы углерода двумерного материала графена расположены в виде сот.
Кристаллические классы
Названия классов гексагональной решетки , нотации Шёнфлиса , нотации Германа-Могена , нотации орбифолда , нотации Коксетера и группы обоев перечислены в таблице ниже.
| Геометрический класс, точечная группа | Группы обоев | ||||
|---|---|---|---|---|---|
| Шён. | Международный | Шар. | Кокс. | ||
| С 3 | 3 | (33) | [3] + | стр.3 (333) | |
| Д 3 | 3м | (*33) | [3] | п3м1 (*333) | стр31м (3*3) |
| С 6 | 6 | (66) | [6] + | стр.6 (632) | |
| Д 6 | 6мм | (*66) | [6] | стр.6м (*632) | |
Смотрите также
- Квадратная решетка
- Шестиугольная мозаика
- Плотная упаковка
- Центрированное шестиугольное число
- Целое число Эйзенштейна
- Диаграмма Вороного
- постоянная Эрмита
Ссылки
- ^ ab Rana, Farhan. "Решетки в 1D, 2D и 3D" (PDF) . Корнелльский университет . Архивировано (PDF) из оригинала 2020-12-18.




