Контактная механика
| Часть серии статей о |
| Механика сплошной среды |
|---|

Контактная механика изучает деформацию твердых тел , которые соприкасаются друг с другом в одной или нескольких точках. [1] [2] Основное различие в контактной механике заключается в различиях между напряжениями, действующими перпендикулярно поверхностям соприкасающихся тел (известными как нормальное напряжение ), и фрикционными напряжениями, действующими по касательной между поверхностями ( напряжение сдвига ). Нормальная контактная механика или механика контакта без трения фокусируется на нормальных напряжениях, вызванных приложенными нормальными силами и адгезией, присутствующей на поверхностях, находящихся в тесном контакте, даже если они чистые и сухие. Фрикционная контактная механика подчеркивает влияние сил трения.
Контактная механика является частью машиностроения . Физическая и математическая формулировка предмета основана на механике материалов и механике сплошных сред и фокусируется на вычислениях, включающих упругие , вязкоупругие и пластичные тела в статическом или динамическом контакте. Контактная механика предоставляет необходимую информацию для безопасного и энергоэффективного проектирования технических систем и для изучения трибологии , контактной жесткости , электрического контактного сопротивления и твердости вдавливания . Принципы контактной механики реализуются в таких приложениях, как контакт колеса-рельса локомотива, сцепные устройства, тормозные системы, шины , подшипники , двигатели внутреннего сгорания , механические связи , прокладки , металлообработка , формовка металлов, ультразвуковая сварка , электрические контакты и многие другие. Текущие проблемы, с которыми сталкиваются в этой области, могут включать анализ напряжений контактных и соединительных элементов и влияние смазки и конструкции материала на трение и износ . Приложения контактной механики далее распространяются в микро- и нанотехнологическую сферу.
Первоначальная работа по контактной механике датируется 1881 годом, когда была опубликована статья «О контакте упругих твердых тел» [3] «Über die Berührung fester elastischer Körper» Генриха Герца . Герц пытался понять, как оптические свойства нескольких, сложенных друг на друга линз могут изменяться в зависимости от силы, удерживающей их вместе. Контактное напряжение Герца относится к локализованным напряжениям, которые возникают, когда две изогнутые поверхности соприкасаются и слегка деформируются под действием приложенных нагрузок. Эта величина деформации зависит от модуля упругости материала, находящегося в контакте. Она дает контактное напряжение как функцию нормальной контактной силы, радиусов кривизны обоих тел и модуля упругости обоих тел. Контактное напряжение Герца составляет основу уравнений для несущей способности и усталостной долговечности в подшипниках, зубчатых передачах и любых других телах, где две поверхности соприкасаются.
История

Классическая контактная механика наиболее известна как Генрих Герц. [3] [4] В 1882 году Герц решил задачу контакта двух упругих тел с искривленными поверхностями. Это все еще актуальное классическое решение дает основу для современных проблем контактной механики. Например, в машиностроении и трибологии контактное напряжение Герца является описанием напряжения внутри сопряженных деталей. Контактное напряжение Герца обычно относится к напряжению, близкому к области контакта между двумя сферами разных радиусов.
Лишь почти сто лет спустя Кеннет Л. Джонсон , Кевин Кендалл и Алан Д. Робертс нашли аналогичное решение для случая адгезионного контакта. [5] Эта теория была отвергнута Борисом Дерягиным и его коллегами [6], которые предложили другую теорию адгезии [7] в 1970-х годах. Модель Дерягина стала известна как модель Дерягина–Мюллера–Топорова (DMT) (в честь Дерягина, М. В. Мюллера и Ю. П. Топорова), [7] а модель Джонсона и др. стала известна как модель Джонсона–Кендалла–Робертса (JKR) для адгезионного упругого контакта. Это отклонение оказалось полезным для разработки параметров Дэвида Табора [8] и позднее Дэниела Моугиса [6] [9] , которые количественно определяют, какая модель контакта (из моделей JKR и DMT) лучше представляет адгезионный контакт для конкретных материалов.
Дальнейшее развитие в области контактной механики в середине двадцатого века можно приписать таким именам, как Фрэнк Филипп Боуден и Табор. Боуден и Табор были первыми, кто подчеркнул важность шероховатости поверхности для контактирующих тел. [10] [11] Благодаря исследованию шероховатости поверхности было обнаружено, что истинная площадь контакта между трущимися партнерами меньше кажущейся площади контакта. Такое понимание также радикально изменило направление начинаний в трибологии. Работы Боудена и Табора привели к появлению нескольких теорий в контактной механике шероховатых поверхностей.
Вклад JF Archard (1957) [12] также следует упомянуть при обсуждении пионерских работ в этой области. Archard пришел к выводу, что даже для шероховатых эластичных поверхностей площадь контакта приблизительно пропорциональна нормальной силе . Дальнейшие важные идеи в этом направлении были предоставлены Jonh A. Greenwood и JBP Williamson (1966), [13] AW Bush (1975), [14] и Bo NJ Persson (2002). [15] Главные выводы этих работ заключались в том, что истинная поверхность контакта в шероховатых материалах, как правило, пропорциональна нормальной силе, в то время как параметры отдельных микроконтактов (давление и размер микроконтакта) лишь слабо зависят от нагрузки.
Классические решения для неадгезивного эластичного контакта
Теория контакта между упругими телами может быть использована для нахождения контактных площадей и глубин вдавливания для простых геометрий. Некоторые часто используемые решения перечислены ниже. Теория, используемая для вычисления этих решений, обсуждается далее в статье. Решения для множества других технически значимых форм, например, усеченного конуса, изношенной сферы, грубых профилей, полых цилиндров и т. д., можно найти в [16]
Контакт между сферой и полупространством
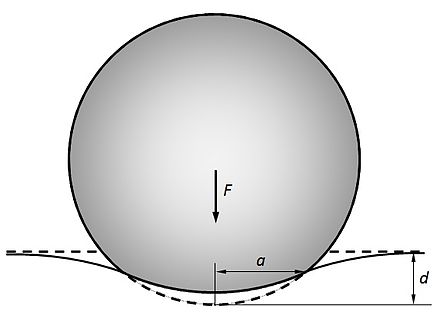
Упругая сфера радиуса вдавливается в упругое полупространство , где общая деформация составляет , в результате чего образуется контактная область радиусом
Приложенная сила связана со смещением соотношением [4]
где
и , — модули упругости , а , — коэффициенты Пуассона , связанные с каждым телом.
Распределение нормального давления в зоне контакта в зависимости от расстояния от центра круга равно [1]
где максимальное контактное давление определяется по формуле
Радиус окружности связан с приложенной нагрузкой уравнением
Общая деформация связана с максимальным контактным давлением соотношением
Максимальное касательное напряжение возникает внутри при .
Контакт между двумя сферами


Для контакта между двумя сферами радиусов и область контакта представляет собой окружность радиуса . Уравнения те же, что и для сферы, контактирующей с полуплоскостью, за исключением того, что эффективный радиус определяется как [4]
Контакт двух скрещенных цилиндров одинакового радиуса
Это эквивалентно контакту между сферой радиуса и плоскостью .
Контакт между жестким цилиндром с плоским концом и упругим полупространством

Если жесткий цилиндр вдавливается в упругое полупространство, то создается распределение давления, описываемое уравнением [17]
где - радиус цилиндра и
Соотношение между глубиной вдавливания и нормальной силой определяется выражением
Контакт между жестким коническим индентором и упругим полупространством

В случае индентирования упругого полупространства с модулем Юнга жестким коническим индентором глубина области контакта и радиус контакта связаны соотношением [17]
с определяемым как угол между плоскостью и боковой поверхностью конуса. Общая глубина отпечатка определяется по формуле:
Полная сила равна
Распределение давления определяется выражением
Напряжение имеет логарифмическую особенность на вершине конуса.
Контакт между двумя цилиндрами с параллельными осями

При контакте двух цилиндров с параллельными осями сила линейно пропорциональна длине цилиндров L и глубине вмятины d : [18]
Радиусы кривизны полностью отсутствуют в этом соотношении. Радиус контакта описывается через обычное соотношение
с
как при контакте двух сфер. Максимальное давление равно
Контакт подшипника
В случае подшипников контакт часто представляет собой контакт между выпуклой поверхностью (наружный цилиндр или сфера) и вогнутой поверхностью (внутренний цилиндр или сфера: отверстие или полусферическая чашка ).
Метод понижения размерности

Некоторые контактные задачи могут быть решены методом понижения размерности (МПР). В этом методе исходная трехмерная система заменяется контактом тела с линейно-упругим или вязкоупругим основанием (см. рис.). Свойства одномерных систем в точности совпадают со свойствами исходной трехмерной системы, если изменить форму тел и определить элементы основания по правилам МПР. [19] [20] МПР основан на решении осесимметричных контактных задач, впервые полученном Людвигом Фёпплем (1941) и Герхардом Шубертом (1942) [21]
Однако для получения точных аналитических результатов требуется, чтобы контактная задача была осесимметричной, а контакты — компактными.
Теория Герца о неадгезивном упругом контакте
Классическая теория контакта фокусировалась в первую очередь на неадгезивном контакте, где не допускается возникновение силы натяжения в области контакта, т. е. контактирующие тела могут быть разделены без сил адгезии. Для решения задач контакта, удовлетворяющих условию отсутствия адгезии, использовалось несколько аналитических и численных подходов. Сложные силы и моменты передаются между телами, где они соприкасаются, поэтому проблемы механики контакта могут стать довольно сложными. Кроме того, контактные напряжения обычно являются нелинейной функцией деформации. Для упрощения процедуры решения обычно определяется система отсчета , в которой объекты (возможно, находящиеся в движении относительно друг друга) являются статическими. Они взаимодействуют посредством поверхностных тяг (или давлений/напряжений) на их интерфейсе.
В качестве примера рассмотрим два объекта, которые встречаются на некоторой поверхности в плоскости ( , ) с осью , предполагаемой нормальной к поверхности. Одно из тел будет испытывать нормально направленное распределение давления и распределение поверхностного натяжения в плоскости и по области . В терминах ньютоновского баланса сил силы:
должны быть равны и противоположны силам, действующим в другом теле. Моменты, соответствующие этим силам:
также должны компенсировать друг друга между телами, чтобы они были кинематически неподвижны.
Предположения в теории Герца
При определении решений контактных задач Герца делаются следующие предположения :
- Деформации невелики и находятся в пределах упругости.
- Поверхности непрерывны и неконформны (это означает, что площадь контакта намного меньше характерных размеров соприкасающихся тел).
- Каждое тело можно рассматривать как упругое полупространство.
- Поверхности не имеют трения.
Дополнительные осложнения возникают, когда некоторые или все эти предположения нарушаются, и такие проблемы контакта обычно называют негерцевскими .
Методы аналитического решения

Аналитические методы решения проблемы неадгезивного контакта можно разделить на два типа в зависимости от геометрии области контакта. [22] Конформный контакт — это тот, в котором два тела соприкасаются в нескольких точках до того, как произойдет какая-либо деформация (т. е. они просто «подходят друг другу»). Неконформный контакт — это тот, в котором формы тел настолько различны, что при нулевой нагрузке они соприкасаются только в точке (или, возможно, вдоль линии). В неконформном случае область контакта мала по сравнению с размерами объектов, и напряжения сильно сконцентрированы в этой области. Такой контакт называется концентрированным , в противном случае он называется диверсифицированным .
Обычный подход в линейной упругости заключается в наложении ряда решений, каждое из которых соответствует точечной нагрузке, действующей на область контакта. Например, в случае нагрузки полуплоскости решение Фламана часто используется в качестве отправной точки, а затем обобщается на различные формы области контакта. Балансы сил и моментов между двумя телами в контакте действуют как дополнительные ограничения решения.
Точечный контакт на (2D) полуплоскости

Отправной точкой для решения контактных задач является понимание эффекта «точечной нагрузки», приложенной к изотропной, однородной и линейно-упругой полуплоскости, показанной на рисунке справа. Проблема может быть либо плоским напряжением , либо плоской деформацией . Это краевая задача линейной упругости, подчиненная граничным условиям натяжения :
где — дельта-функция Дирака . Граничные условия устанавливают, что на поверхности нет касательных напряжений, а сингулярная нормальная сила P приложена в точке (0, 0). Применение этих условий к основным уравнениям упругости дает результат
для некоторой точки, , в полуплоскости. Окружность, показанная на рисунке, обозначает поверхность, на которой максимальное касательное напряжение постоянно. Из этого поля напряжений можно определить компоненты деформации и, следовательно, смещения всех материальных точек.
Линейный контакт на (2D) полуплоскости
Нормальная загрузка по региону
Предположим, что вместо точечной нагрузки к поверхности приложена распределенная нагрузка в диапазоне . Принцип линейной суперпозиции можно применить для определения результирующего поля напряжений как решения интегральных уравнений:
Сдвиговая нагрузка по области
Тот же принцип применим к нагрузке на поверхность в плоскости поверхности. Эти виды тяги, как правило, возникают в результате трения. Решение аналогично вышеприведенному (как для единичных нагрузок, так и для распределенных нагрузок ), но немного изменено:
Эти результаты можно наложить на приведенные выше для нормальной нагрузки, чтобы иметь дело с более сложными нагрузками.
Точечный контакт на (3D) полупространстве
Аналогично решению Фламана для 2D полуплоскости, фундаментальные решения известны и для линейно-упругого 3D полупространства. Они были найдены Буссинеском для сосредоточенной нормальной нагрузки и Черрути для касательной нагрузки. См. раздел об этом в Линейной упругости .
Методы численного решения
Различия между согласованным и несогласованным контактом не должны проводиться, когда численные схемы решения используются для решения контактных задач. Эти методы не полагаются на дополнительные предположения в процессе решения, поскольку они базируются исключительно на общей формулировке основных уравнений. [23] [24] [25] [26] [27] Помимо стандартных уравнений, описывающих деформацию и движение тел, можно сформулировать два дополнительных неравенства. Первое просто ограничивает движение и деформацию тел предположением, что проникновение не может произойти. Следовательно, зазор между двумя телами может быть только положительным или нулевым
где обозначает контакт. Второе предположение в контактной механике связано с тем, что в области контакта не допускается возникновение силы натяжения (контактирующие тела могут быть подняты без сил адгезии). Это приводит к неравенству, которому должны подчиняться напряжения на контактном интерфейсе. Оно сформулировано для нормального напряжения .
В местах, где поверхности соприкасаются, зазор равен нулю, т. е . , и там нормальное напряжение отлично от нуля, действительно, . В местах, где поверхности не соприкасаются, нормальное напряжение идентично нулю; , в то время как зазор положителен; т. е . . Этот тип формулировки дополнительности может быть выражен в так называемой форме Куна–Таккера , а именно.
Эти условия справедливы в общем случае. Математическая формулировка зазора зависит от кинематики базовой теории твердого тела (например, линейного или нелинейного твердого тела в двух- или трех измерениях, модели балки или оболочки ). Переформулировав нормальное напряжение в терминах контактного давления, ; т. е. задачу Куна-Таккера можно переформулировать в стандартной форме дополнительности, т. е. В линейно-упругом случае зазор можно сформулировать как , где - разделение жесткого тела, - геометрия/топография контакта (цилиндр и шероховатость), а - упругая деформация/прогиб. Если контактирующие тела аппроксимируются как линейные упругие полупространства, решение интегрального уравнения Буссинеска-Черрути можно применить для выражения деформации ( ) как функции контактного давления ( ); т. е. где для линейной нагрузки упругого полупространства и для точечной нагрузки упругого полупространства. [1]
После дискретизации задача линейной упругой контактной механики может быть сформулирована в стандартной форме линейной задачи дополнительности (ЛПВ). [28]
где — матрица, элементами которой являются так называемые коэффициенты влияния, связывающие контактное давление и деформацию. Строгая формулировка LCP задачи CM, представленная выше, позволяет напрямую применять общепризнанные методы численного решения, такие как алгоритм поворота Лемке . Алгоритм Лемке имеет то преимущество, что он находит численно точное решение в течение конечного числа итераций. Реализация MATLAB, представленная Almqvist et al., является одним из примеров, который можно использовать для численного решения задачи. Кроме того, пример кода для решения LCP задачи линейной упругой контактной механики 2D также был опубликован на файлообменнике MATLAB Almqvist et al.
Контакт между шероховатыми поверхностями
Когда два тела с шероховатыми поверхностями прижимаются друг к другу, истинная площадь контакта, образованная между двумя телами, , намного меньше кажущейся или номинальной площади контакта . Механика контактирующих шероховатых поверхностей обсуждается с точки зрения нормальной механики контакта и статических фрикционных взаимодействий. [29] Естественные и инженерные поверхности обычно демонстрируют шероховатости, известные как неровности, в широком диапазоне масштабов длины вплоть до молекулярного уровня, при этом поверхностные структуры демонстрируют самосродство, также известное как поверхностная фрактальность . Признано, что самосродство структуры поверхностей является источником линейного масштабирования истинной площади контакта с приложенным давлением. [30] [31] Предполагая модель сдвиговых сварных контактов в трибологических взаимодействиях, эту повсеместно наблюдаемую линейность между площадью контакта и давлением можно также считать источником линейности соотношения между статическим трением и приложенной нормальной силой. [29]
При контакте между «случайной шероховатой» поверхностью и упругим полупространством истинная площадь контакта связана с нормальной силой соотношением [1] [31] [32] [33]
с равным среднему квадратному корню (также известному как среднее квадратичное) наклона поверхности и . Срединное давление в истинной контактной поверхности
можно обоснованно оценить как половину эффективного модуля упругости , умноженного на среднеквадратический уклон поверхности .
Обзор модели GW
Гринвуд и Уильямсон в 1966 году (GW) [31] предложили теорию упругой контактной механики шероховатых поверхностей, которая сегодня является основой многих теорий в трибологии (трение, адгезия, тепловая и электропроводность, износ и т. д.). Они рассмотрели контакт между гладкой жесткой плоскостью и номинально плоской деформируемой шероховатой поверхностью, покрытой круглыми вершинами неровностей того же радиуса R. Их теория предполагает, что деформация каждой неровности независима от деформации ее соседей и описывается моделью Герца. Высоты неровностей имеют случайное распределение. Вероятность того, что высота неровности находится между и равна . Авторы вычислили количество пятен контакта n, общую площадь контакта и общую нагрузку P в общем случае. Они привели эти формулы в двух формах: в базовой и с использованием стандартизированных переменных. Если предположить, что N неровностей покрывают шероховатую поверхность, то ожидаемое количество контактов равно
Ожидаемую общую площадь контакта можно рассчитать по формуле
и ожидаемая общая сила определяется как
где:
- R, радиус кривизны микронеровности,
- z, высота микронеровности, измеренная от линии профиля,
- г, закрыть поверхность,
- , составной модуль упругости Юнга,
- , модуль упругости поверхности,
- , Коэффициенты поверхности Пуассона.
Гринвуд и Уильямсон ввели стандартизированное разделение и стандартизированное распределение высот , стандартное отклонение которых равно единице. Ниже представлены формулы в стандартизированном виде.
где:
- d — это разделение,
- номинальная площадь контакта,
- - поверхностная плотность неровностей,
- — эффективный модуль Юнга.
и могут быть определены, когда термины вычисляются для данных поверхностей с использованием свертки шероховатости поверхности . [34] Несколько исследований следовали предложенным кривым подгонкам для предположения о высоком распределении гауссовой поверхности с кривыми подгонками, представленными Аркуманисом и др. [35] и Йедынаком [36] среди других. Неоднократно наблюдалось, что инженерные поверхности не демонстрируют гауссовы распределения высот поверхности, например, Пекленик. [37] Лейтон и др. [38] представили подгонки для поверхностей цилиндров двигателей внутреннего сгорания с перекрестной штриховкой вместе с процессом определения терминов для любых измеренных поверхностей. Лейтон и др. [38] продемонстрировали, что данные гауссовой подгонки неточны для моделирования любых инженерных поверхностей, и продолжили демонстрировать [39] , что раннее движение поверхностей приводит к постепенному переходу, который значительно изменяет топографию поверхности, несущую способность и трение.
Недавно точные аппроксиманты и были опубликованы Jedynak. [36] Они задаются следующими рациональными формулами, которые являются аппроксимантами интегралов . Они вычисляются для гауссовского распределения неровностей, которые, как было показано, нереалистичны для инженерной поверхности, но могут быть приняты там, где результаты трения, грузоподъемности или реальной площади контакта не являются критическими для анализа. [38]
Для коэффициентов есть
Максимальная относительная погрешность составляет .
Для коэффициентов есть
Максимальная относительная погрешность составляет . В статье [36] также приведены точные выражения для
где erfc(z) означает дополнительную функцию ошибок, а — модифицированная функция Бесселя второго рода.
Для ситуации, когда неровности на двух поверхностях имеют гауссово распределение высот, а пики можно считать сферическими, [31] среднее контактное давление достаточно, чтобы вызвать текучесть, когда где — одноосный предел текучести , а — твердость при вдавливании. [1] Гринвуд и Уильямсон [31] определили безразмерный параметр , называемый индексом пластичности , который можно использовать для определения того, будет ли контакт упругим или пластичным.
Модель Гринвуда-Вильямсона требует знания двух статистически зависимых величин: стандартного отклонения шероховатости поверхности и кривизны пиков неровностей. Альтернативное определение индекса пластичности было дано Микичом. [32] Текучесть происходит, когда давление больше одноосного предела текучести. Поскольку предел текучести пропорционален твердости вдавливания , Микич определил индекс пластичности для упруго-пластического контакта как
В этом определении представлена микрошероховатость в состоянии полной пластичности и требуется только одна статистическая величина, среднеквадратичный наклон, который можно рассчитать из измерений поверхности. Для поверхность ведет себя упруго во время контакта.
В обеих моделях Гринвуда-Вильямсона и Микича предполагается, что нагрузка пропорциональна деформированной области. Следовательно, то, ведет ли себя система пластично или упруго, не зависит от приложенной нормальной силы. [1]
Обзор модели GT
Модель, предложенная Джоном А. Гринвудом и Джоном Х. Триппом (GT), [40] расширила модель GW до контакта между двумя шероховатыми поверхностями. Модель GT широко используется в области эластогидродинамического анализа.
Наиболее часто цитируемые уравнения, полученные с помощью модели GT, относятся к области контакта неровностей.
и нагрузка, переносимая неровностями
где:
- , параметр шероховатости,
- , номинальная площадь контакта,
- , Параметр масляной пленки Штрибека, впервые определенный Штрибеком \cite{gt} как ,
- , эффективный модуль упругости,
- , статистические функции, введенные для соответствия предполагаемому гауссовому распределению неровностей.
Мэтью Лейтон и др. [38] представили подгонки для поверхностей цилиндров двигателя внутреннего сгорания с перекрестной штриховкой вместе с процессом определения условий для любых измеренных поверхностей. Лейтон и др. [38] продемонстрировали, что данные подгонки Гаусса неточны для моделирования любых спроектированных поверхностей, и продолжили демонстрировать [39] , что раннее прохождение поверхностей приводит к постепенному переходу, который существенно изменяет топографию поверхности, несущую способность и трение.
Точные решения для и впервые представлены Едынаком. [36] Они выражаются следующим образом. Они рассчитаны для гауссовского распределения неровностей, которые, как было показано, нереалистичны для инженерной поверхности, но могут быть приняты там, где результаты трения, грузоподъемности или реальной площади контакта не являются критическими для анализа. [38]
где erfc(z) означает дополнительную функцию ошибок, а — модифицированная функция Бесселя второго рода.
В статье [36] можно найти всесторонний обзор существующих аппроксимаций для . Новые предложения дают наиболее точные аппроксимации для и , о которых сообщается в литературе. Они даются следующими рациональными формулами, которые являются очень точными аппроксимациями для интегралов . Они вычисляются для гауссовского распределения неровностей
Для коэффициентов есть
Максимальная относительная погрешность составляет .
Для коэффициентов есть
Максимальная относительная погрешность составляет .
Адгезионный контакт между эластичными телами
Когда две твердые поверхности находятся в непосредственной близости, они испытывают притягивающие силы Ван-дер-Ваальса . Модель Ван-дер-Ваальса RS Bradley [41] дает возможность рассчитать силу натяжения между двумя жесткими сферами с идеально гладкими поверхностями. Модель контакта Герца не считает адгезию возможной. Однако в конце 1960-х годов было обнаружено несколько противоречий, когда теорию Герца сравнивали с экспериментами, включающими контакт между резиновыми и стеклянными сферами.
Было отмечено [5] , что, хотя теория Герца применима при больших нагрузках, при малых нагрузках
- площадь контакта оказалась больше, чем предсказывала теория Герца,
- площадь контакта имела ненулевое значение даже при снятии нагрузки, и
- даже если соприкасающиеся поверхности были чистыми и сухими, адгезия была сильной.
Это указывало на то, что действуют адгезионные силы. Модель Джонсона-Кендалла-Робертса (JKR) и модели Дерягина-Мюллера-Топорова (DMT) были первыми, кто включил адгезию в контакт Герца.
Модель жесткого контакта Брэдли
Обычно предполагается, что поверхностная сила между двумя атомными плоскостями на расстоянии друг от друга может быть выведена из потенциала Леннарда-Джонса . При таком предположении
где — сила (положительная при сжатии), — полная поверхностная энергия обеих поверхностей на единицу площади, — равновесное разделение двух атомных плоскостей.
Модель Брэдли применила потенциал Леннарда-Джонса для нахождения силы сцепления между двумя жесткими сферами. Общая сила между сферами оказывается равной
где — радиусы двух сфер.
Две сферы полностью разделяются, когда достигается сила отрыва , в этой точке
Модель упругого контакта JKR


Чтобы включить эффект адгезии в контакт Герца, Джонсон, Кендалл и Робертс [5] сформулировали теорию адгезионного контакта JKR, используя баланс между запасенной упругой энергией и потерей поверхностной энергии . Модель JKR учитывает эффект контактного давления и адгезии только внутри области контакта. Общее решение для распределения давления в области контакта в модели JKR имеет вид
Обратите внимание, что в оригинальной теории Герца термин «содержащий» был опущен на том основании, что в зоне контакта не может поддерживаться напряжение. Для контакта двух сфер
где - радиус области контакта, - приложенная сила, - полная поверхностная энергия обеих поверхностей на единицу площади контакта, - радиусы, модули Юнга и коэффициенты Пуассона двух сфер, и
Расстояние сближения между двумя сферами определяется по формуле
Уравнение Герца для площади контакта двух сфер, модифицированное с учетом поверхностной энергии, имеет вид
Когда поверхностная энергия равна нулю, , уравнение Герца для контакта между двумя сферами восстанавливается. Когда приложенная нагрузка равна нулю, радиус контакта равен
Растягивающая нагрузка, при которой сферы разделяются (т.е. ), по прогнозам, составит
Эту силу также называют силой отрыва . Обратите внимание, что эта сила не зависит от модулей двух сфер. Однако существует и другое возможное решение для значения при этой нагрузке. Это критическая площадь контакта , определяемая как
Если мы определим работу адгезии как
где — энергии сцепления двух поверхностей, а — член взаимодействия, мы можем записать радиус контакта JKR как
Растягивающая нагрузка при отрыве составляет
а критический радиус контакта определяется как
Критическая глубина проникновения составляет
Модель упругого контакта DMT
Модель Дерягина–Мюллера–Топорова (ДМТ) [7] [42] представляет собой альтернативную модель адгезионного контакта, которая предполагает, что профиль контакта остается таким же, как и при контакте по Герцу, но с дополнительными притягивающими взаимодействиями за пределами области контакта.
Радиус контакта между двумя сферами из теории ДМТ равен
и сила отрыва равна
При достижении силы отрыва площадь контакта становится равной нулю, и на краю площади контакта отсутствует сингулярность контактных напряжений.
С точки зрения работы адгезии
и
Параметр Табора
В 1977 году Табор [43] показал, что кажущееся противоречие между теориями JKR и DMT можно разрешить, отметив, что эти две теории являются крайними пределами одной теории, параметризованной параметром Табора ( ), определяемым как
где — равновесное разделение между двумя соприкасающимися поверхностями. Теория JKR применяется к большим, податливым сферам, для которых велико. Теория DMT применяется к маленьким, жестким сферам с малыми значениями .
Впоследствии Дерягин и его коллеги [44] , применив закон поверхностной силы Брэдли к упругому полупространству, подтвердили, что по мере увеличения параметра Табора сила отрыва падает от значения Брэдли до значения JKR . Более подробные расчеты были позже выполнены Гринвудом [45], выявившим S-образную кривую нагрузки/подхода, которая объясняет эффект прыжка. Более эффективный метод выполнения расчетов и дополнительные результаты были предоставлены Фэном [46].
Модель упругого контакта Моугиса–Дагдейла

Дальнейшее усовершенствование идеи Табора было сделано Могисом [9], который представил поверхностную силу в терминах приближения зоны сцепления Дагдейла, так что работа адгезии определяется выражением
где — максимальная сила, предсказанная потенциалом Леннарда-Джонса, а — максимальное разделение, полученное путем сопоставления областей под кривыми Дагдейла и Леннарда-Джонса (см. соседний рисунок). Это означает, что сила притяжения постоянна для . Дальнейшего проникновения при сжатии не происходит. Идеальный контакт происходит в области радиусом , а силы адгезии величиной распространяются на область радиусом . В области две поверхности разделены расстоянием с и . Отношение определяется как
- .
В теории Маугиса–Дагдейла [47] распределение поверхностного натяжения делится на две части — одна из-за контактного давления Герца, а другая из-за адгезионного напряжения Дагдейла. Контакт Герца предполагается в области . Вклад в поверхностное натяжение от давления Герца определяется выражением
где контактная сила Герца определяется выражением
Проникновение из-за упругого сжатия равно
Вертикальное смещение при этом равно
и расстояние между двумя поверхностями равно
Распределение поверхностного натяжения из-за адгезионного напряжения Дагдейла равно
Тогда общая сила сцепления определяется по формуле
Сжатие из-за адгезии Дагдейла равно
и разрыв в составляет
Чистое сцепление на контактной поверхности тогда определяется как , а чистая сила контакта равна . Когда адгезионное сцепление падает до нуля.
На этом этапе вводятся безразмерные значения , которые определяются как
Кроме того, Маугис предложил параметр , который эквивалентен параметру Табора . Этот параметр определяется как
где ступенчатое когезионное напряжение равно теоретическому напряжению потенциала Леннарда-Джонса
Чжэн и Юй [48] предложили другое значение для ступенчатого когезионного напряжения
чтобы соответствовать потенциалу Леннарда-Джонса, что приводит к
Тогда чистая сила контакта может быть выражена как
и упругое сжатие как
Уравнение для зазора сцепления между двумя телами принимает вид
Это уравнение можно решить, чтобы получить значения для различных значений и . Для больших значений и получается модель JKR. Для малых значений извлекается модель DMT.
Модель Карпика-Оглтри-Салмерона (COS)
Модель Могиса–Дагдейла может быть решена только итеративно, если значение неизвестно априори. Приближенное решение Карпика–Оглетри–Салмерона (COS) [49] (по Роберту Карпику , Д. Фрэнку Оглетри и Микелю Салмерону) упрощает процесс, используя следующее соотношение для определения радиуса контакта :
где - площадь контакта при нулевой нагрузке, а - параметр перехода, связанный с соотношением
Случай точно соответствует теории JKR, а соответствует теории DMT. Для промежуточных случаев модель COS близко соответствует решению Маугиса–Дагдейла для .
Влияние формы контакта
Даже при наличии идеально гладких поверхностей геометрия может играть роль в виде макроскопической формы контактирующей области. Когда жесткий штамп с плоской, но странной формы поверхностью осторожно отрывается от его мягкого аналога, его отрыв происходит не мгновенно, а фронты отрыва начинаются с заостренных углов и движутся внутрь, пока не будет достигнута конечная конфигурация, которая для макроскопически изотропных форм является почти круглой. Основным параметром, определяющим прочность сцепления плоских контактов, оказывается максимальный линейный размер контакта. [50] Процесс отрыва можно, как это экспериментально наблюдается, увидеть на пленке. [51]
Смотрите также
- Клей – неметаллический материал, используемый для склеивания различных материалов.
- Склеивание – метод соединения, используемый при производстве и ремонте.
- Адгезионная железная дорога – железная дорога, использующая адгезию для движения поездов.
- Адгезионные поверхностные силы – Молекулярные свойства
- Несущая способность – способность почвы выдерживать нагрузки.
- Столкновение – случай, когда два или более тел физически контактируют друг с другом в течение короткого периода времени.
- Динамика контакта – Движение многотельных систем
- Контактное сопротивление – электрическое сопротивление, приписываемое контактным интерфейсам (ECR)
- Дисперсионная адгезия – адгезия между материалами за счет межмолекулярного взаимодействия.
- Электростатический генератор – устройство, генерирующее электрический заряд на высоковольтном электроде.
- Энергетически модифицированный цемент – класс цементов, механически обработанных для преобразования реакционной способности.
- Механика фрикционного контакта – изучение деформации тел при наличии эффектов трения.
- Фрикционный привод – механическая передача энергии посредством трения между компонентами.
- Истирание – вид износа, вызванный адгезией между скользящими поверхностями.
- Гониометр – прибор для измерения углов
- Негладкая механика – Подход к моделированию в механике
- Прокатка (металлообработка) – процесс обработки металлов давлением
- Удар (механика) – Внезапное кратковременное ускорение
- Задача Синьорини – Задача эластостатики в линейной упругости
- Поверхностное натяжение – тенденция поверхности жидкости к сжатию с целью уменьшения площади поверхности.
- Трибология – наука и техника взаимодействующих поверхностей в относительном движении.
- Односторонний контакт – Механическое ограничение, которое препятствует проникновению между двумя телами.
- Смачивание — способность жидкости поддерживать контакт с твердой поверхностью.
Ссылки
- ^ abcdef Джонсон, К. Л. (1985). Контактная механика . Издательство Кембриджского университета. ISBN 978-0-521-25576-9.
- ^ Попов, ВЛ (2010). Контактная механика и трение: физические принципы и приложения . Springer Berlin Heidelberg. стр. 362. ISBN 978-3-642-10803-7.
- ^ ab H. Hertz, 1881, Über die berührung fester elastischer Körper, Journal für die reine und angewandte Mathematik 92, стр. 156-171. (Английскую версию см.: Hertz, H., 1896. О контакте упругих твердых тел, В: Miscellaneous Papers, Chapter V, стр. 146–162 . Герц, Х. и Ленард П., перевод Джонса, DE. и Шотт Г.А., Лондон: Macmillan.
- ^ abc Hertz, HR, 1882, Über die Berührung fester elastischer Körper und Über die Härte, Verhandlungen des Vereins zur Beförderung des Gewerbefleisscs , Берлин: Verein zur Beförderung des Gewerbefleisses, стр. 449–463 (английскую версию см.: Герц, Х., 1896. О контакте твердых упругих тел и твердости, В: Разные статьи, глава VI, стр. 163–183 , авторы: Герц Х. и Ленард П., перевод Джонса Д.Э. и Шотта Г.А. , Лондон: Макмиллан.
- ^ abc Джонсон, К. Л.; Кендалл, К.; Робертс, А. Д. (1971-09-08). «Поверхностная энергия и контакт упругих твердых тел». Труды Лондонского королевского общества. A. Математические и физические науки . 324 (1558). Королевское общество: 301– 313. Bibcode : 1971RSPSA.324..301J. doi : 10.1098/rspa.1971.0141 . ISSN 0080-4630. S2CID 137730057.
- ^ ab Maugis, D. (2000-02-03). Контакт, адгезия и разрыв упругих твердых тел . Springer Science & Business Media. ISBN 3-540-66113-1.
- ^ abc Дерягин, Б.В.; Мюллер, В.М.; Топоров, Ю.П. (1975). "Влияние контактных деформаций на адгезию частиц". Journal of Colloid and Interface Science . 53 (2). Elsevier BV: 314– 326. Bibcode :1975JCIS...53..314D. doi :10.1016/0021-9797(75)90018-1. ISSN 0021-9797.
- ^ Табор, Д (1970-01-01). «Твёрдость твёрдых тел». Обзоры физики в технике . 1 (3). Издательство IOP: 145–179 . doi :10.1088/0034-6683/1/3/i01. ISSN 0034-6683.
- ^ ab Maugis, Daniel (1992). «Адгезия сфер: переход JKR-DMT с использованием модели Дагдейла». Журнал коллоидной и интерфейсной науки . 150 (1). Elsevier BV: 243– 269. Bibcode : 1992JCIS..150..243M. doi : 10.1016/0021-9797(92)90285-t. ISSN 0021-9797.
- ^ "Площадь контакта между неподвижными и движущимися поверхностями". Труды Лондонского королевского общества. Серия A. Математические и физические науки . 169 (938). Королевское общество: 391– 413. 1939-02-07. doi :10.1098/rspa.1939.0005. ISSN 0080-4630.
- ^ Боуден, Ф. П.; Табор, Д. (2001). Трение и смазка твердых тел. Международная серия монографий по физике. Том 1. Clarendon Press. ISBN 978-0-19-850777-2.
- ^ Арчард, Дж. Ф. (1957-12-24). «Упругая деформация и законы трения». Труды Лондонского королевского общества. Серия A. Математические и физические науки . 243 (1233). Королевское общество: 190–205 . Bibcode : 1957RSPSA.243..190A. doi : 10.1098/rspa.1957.0214. ISSN 0080-4630. S2CID 138707812.
- ^ Гринвуд, JA; Уильямсон, JBP (1966-12-06). «Контакт номинально плоских поверхностей». Труды Лондонского королевского общества. Серия A. Математические и физические науки . 295 (1442). Королевское общество: 300–319 . Bibcode : 1966RSPSA.295..300G. doi : 10.1098/rspa.1966.0242. ISSN 0080-4630. S2CID 137430238.
- ^ Буш, AW; Гибсон, RD; Томас, TR (1975). «Упругий контакт шероховатой поверхности». Wear . 35 (1). Elsevier BV: 87– 111. doi :10.1016/0043-1648(75)90145-3. ISSN 0043-1648.
- ^ Перссон, Б.Н.Дж.; Бухер, Ф.; Кьяйя, Б. (2002-04-29). "Упругий контакт между случайно шероховатыми поверхностями: сравнение теории с численными результатами". Physical Review B. 65 ( 18). Американское физическое общество (APS): 184106. Bibcode : 2002PhRvB..65r4106P. doi : 10.1103/physrevb.65.184106. ISSN 0163-1829.
- ^ Попов, Валентин Л.; Хесс, Маркус; Виллерт, Эмануэль (2019). Справочник контактной механики: Точные решения осесимметричных контактных задач. Берлин Гейдельберг: Springer-Verlag. ISBN 9783662587089.
- ^ ab Sneddon, Ian N. (1965). «Соотношение между нагрузкой и проникновением в осесимметричной задаче Буссинеска для штампа произвольного профиля». Международный журнал инженерных наук . 3 (1). Elsevier BV: 47– 57. doi :10.1016/0020-7225(65)90019-4. ISSN 0020-7225.
- ^ Попов, Валентин Л. (2010-03-10). Контактная механика и трение . Springer Science & Business Media. ISBN 978-3-642-10803-7.
- ^ Попов, Валентин Л. (2013). «Метод снижения размерности в механике контакта и трения: связь между микро- и макромасштабами». Трение . 1 (1). Springer Science and Business Media LLC: 41– 62. doi : 10.1007/s40544-013-0005-3 . ISSN 2223-7690. S2CID 256405038.
- ^ Попов, Валентин Л.; Хесс, Маркус (01 октября 2013 г.). Methode der Dimensionsreduktion in Kontaktmechanik und Reibung (на немецком языке). Спрингер-Верлаг. ISBN 978-3-642-32673-8.
- ^ Попова, Елена; Попов, Валентин Львович (2020). «Людвиг Фёппль и Герхард Шуберт: Неизвестные классики контактной механики». ZAMM — Журнал прикладной математики и механики / Zeitschrift für Angewandte Mathematik und Mechanik . 100 (9): e202000203. Бибкод : 2020ZaMM..100E0203P. дои : 10.1002/замм.202000203 .
- ^ Шигли, Джозеф Эдвард; Мишке, Чарльз Р. (1989). "Гл. 2". Проектирование машиностроения (5-е изд.). McGraw-Hill Science, Engineering & Mathematics. ISBN 0-07-056899-5.
- ^ Kalker, JJ (1990). Трехмерные упругие тела в контакте качения. Механика твердого тела и ее приложения. Springer Netherlands. ISBN 978-0-7923-0712-9.
- ^ Wriggers, P. (2006). Computational Contact Mechanics (2-е изд.). Springer Berlin Heidelberg. ISBN 978-3-540-32609-0.
- ^ Laursen, TA (2003). Computational Contact and Impact Mechanics: Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis. Инженерная электронная библиотека. Springer Berlin Heidelberg. ISBN 978-3-540-42906-7.
- ^ Acary, V.; Brogliato, B. (2008). Численные методы для негладких динамических систем: приложения в механике и электронике. Lecture Notes in Applied and Computational Mechanics. Springer Berlin Heidelberg. ISBN 978-3-540-75392-6.
- ^ Попов, Валентин Л. (2009). Kontaktmechanik und Reibung (на немецком языке). Springer Science & Business Media. ISBN 978-3-540-88836-9.
- ^ Коттл, Р.; Панг, Дж.; Стоун, Р. (2009-01-01). Проблема линейной дополнительности . Классика прикладной математики. Общество промышленной и прикладной математики. doi : 10.1137/1.9780898719000. ISBN 9780898716863.
- ^ ab Hanaor, D.; Gan, Y.; Einav, I. (2016). «Статическое трение на фрактальных интерфейсах». Tribology International . 93 : 229–238 . arXiv : 2106.01473 . doi : 10.1016/j.triboint.2015.09.016. S2CID 51900923.
- ^ Zhai, Chongpu; Hanaor, Dorian; Gan, Yixiang (2017). «Контактная жесткость многомасштабных поверхностей с помощью анализа усечения». International Journal of Mechanical Sciences . 131– 132. Elsevier BV: 305– 316. doi :10.1016/j.ijmecsci.2017.07.018. ISSN 0020-7403.
- ^ abcde Гринвуд, JA; Уильямсон, JBP (1966-12-06). «Контакт номинально плоских поверхностей». Труды Лондонского королевского общества. Серия A. Математические и физические науки . 295 (1442). Королевское общество: 300– 319. Bibcode : 1966RSPSA.295..300G. doi : 10.1098/rspa.1966.0242. ISSN 0080-4630. S2CID 137430238.
- ^ ab Mikić, BB (1974). «Проводимость теплового контакта; теоретические соображения». International Journal of Heat and Mass Transfer . 17 (2). Elsevier BV: 205– 214. doi :10.1016/0017-9310(74)90082-9. ISSN 0017-9310.
- ^ Хён, Сангил; Роббинс, Марк О. (2007). «Упругий контакт между шероховатыми поверхностями: влияние шероховатости на больших и малых длинах волн». Tribology International . 40 ( 10–12 ). Elsevier BV: 1413–1422 . doi :10.1016/j.triboint.2007.02.003. ISSN 0301-679X.
- ^ Лейтон и др. (2016). "Факторы потока, зависящие от поверхности, для прогнозирования трения заштрихованных поверхностей" (PDF) . Топография поверхности: метрология и свойства . 4 (2): 025002. Bibcode :2016SuTMP...4b5002L. doi : 10.1088/2051-672x/4/2/025002 . S2CID 111631084.
- ^ Arcoumanis, C.; Ostovar, P.; Mortier, R. (1997-10-01). "Моделирование смешанной смазки ньютоновских и сдвиговых жидкостей в конфигурации поршень-кольцо". Серия технических документов SAE . Том 1. Warrendale, PA. doi :10.4271/972924.
- ^ abcde Jedynak, Radosław (2019). "Точные и приближенные решения бесконечных интегралов распределения высоты неровностей для моделей контакта неровностей Гринвуда-Вильямсона и Гринвуда-Триппа". Tribology International . 130 . Elsevier BV: 206– 215. doi :10.1016/j.triboint.2018.09.009. ISSN 0301-679X. S2CID 139894096.
- ^ Peklenik, J. (сентябрь 1967 г.). "Paper 24: New Developments in Surface Characterization and Measurements by Means of Random Process Analysis" . Труды Института инженеров-механиков, Труды конференции . 182 (11): 108– 126. doi :10.1243/pime_conf_1967_182_309_02. ISSN 0367-8849.
- ^ abcdef Лейтон, М.; Моррис, Н.; Рахмани, Р.; Рахнежат, Х. (2017-01-01). "Модель специфической неровности поверхности для прогнозирования трения в граничных и смешанных режимах смазки" (PDF) . Meccanica . 52 (1): 21– 33. doi :10.1007/s11012-016-0397-z. ISSN 1572-9648. S2CID 54710212.
- ^ ab Лейтон, М; Моррис, Н; Гор, М; Рахмани, Р; Рахнеджат, Х; Кинг, П. Д. (2016-08-05). "Граничные взаимодействия шероховатых негауссовых поверхностей" (PDF) . Труды Института инженеров-механиков, часть J: Журнал инженерной трибологии . 230 (11): 1359– 1370. doi : 10.1177/1350650116656967 . ISSN 1350-6501. S2CID 53347629.
- ^ Гринвуд, JA; Трипп, JH (1970). «Контакт двух номинально плоских шероховатых поверхностей». Труды Института инженеров-механиков . 185 (1). Публикации SAGE: 625– 633. doi :10.1243/pime_proc_1970_185_069_02. ISSN 0020-3483.
- ^ Брэдли, RS (1932). "LXXIX. Сила сцепления между твердыми поверхностями и поверхностная энергия твердых тел ". Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 13 (86). Informa UK Limited: 853– 862. doi : 10.1080/14786449209461990. ISSN 1941-5982.
- ^ Мюллер, В.М.; Дерягин, Б.В.; Топоров, Ю.П. (1983). «О двух методах расчета силы прилипания упругого шара к жесткой плоскости». Коллоиды и поверхности . 7 (3). Elsevier BV: 251– 259. doi :10.1016/0166-6622(83)80051-1. ISSN 0166-6622.
- ^ TABOR, D. (1977). "Поверхностные силы и поверхностные взаимодействия". Пленарные и приглашенные лекции . Elsevier. стр. 3–14. doi :10.1016/b978-0-12-404501-9.50009-2. ISBN 9780124045019.
- ^ Мюллер, В.М.; Ющенко, В.С.; Дерягин, Б.В. (1980). «О влиянии молекулярных сил на деформацию упругой сферы и ее прилипание к жесткой плоскости». Journal of Colloid and Interface Science . 77 (1). Elsevier BV: 91– 101. Bibcode :1980JCIS...77...91M. doi :10.1016/0021-9797(80)90419-1. ISSN 0021-9797.
- ^ Гринвуд, JA (1997-06-08). «Сцепление упругих сфер». Труды Лондонского королевского общества. Серия A: Математические, физические и инженерные науки . 453 (1961). Королевское общество: 1277– 1297. Bibcode : 1997RSPSA.453.1277G. doi : 10.1098/rspa.1997.0070. ISSN 1364-5021. S2CID 124217562.
- ^ Фэн, Джеймс К. (2000). «Контактное поведение сферических упругих частиц: вычислительное исследование адгезии частиц и деформаций». Коллоиды и поверхности A: физико-химические и инженерные аспекты . 172 ( 1–3 ). Elsevier BV: 175–198 . doi :10.1016/s0927-7757(00)00580-x. ISSN 0927-7757.
- ^ Джонсон, К. Л.; Гринвуд, Дж. А. (1997). «Карта адгезии для контакта эластичных сфер». Журнал коллоидной и интерфейсной науки . 192 (2). Elsevier BV: 326– 333. Bibcode : 1997JCIS..192..326J. doi : 10.1006/jcis.1997.4984. ISSN 0021-9797. PMID 9367554.
- ^ Чжэн, Чжицзюнь; Ю, Цзилинь (2007). «Использование приближения Дагдейла для сопоставления определенного взаимодействия в адгезионном контакте эластичных объектов». Журнал коллоидной и интерфейсной науки . 310 (1). Elsevier BV: 27– 34. Bibcode : 2007JCIS..310...27Z. doi : 10.1016/j.jcis.2007.01.042. ISSN 0021-9797. PMID 17335843.
- ^ Карпик, Роберт В.; Оглтри, Д. Франк; Салмерон, Микель (1999). «Общее уравнение для подгонки контактной площади и трения против измерений нагрузки». Журнал коллоидной и интерфейсной науки . 211 (2). Elsevier BV: 395– 400. Bibcode : 1999JCIS..211..395C. doi : 10.1006/jcis.1998.6027. ISSN 0021-9797. PMID 10049556.
- ^ Попов, Валентин Л.; Похрт, Роман; Ли, Цян (2017-09-01). "Прочность адгезионных контактов: влияние геометрии контакта и градиентов материалов". Трение . 5 (3): 308–325 . doi : 10.1007/s40544-017-0177-3 . ISSN 2223-7690.
- ^ Friction Physics (2017-12-06). Научное трение: Адгезия сложных форм. Архивировано из оригинала 2021-12-15 . Получено 2018-01-02 – через YouTube.
Внешние ссылки
- [1]: Процедура MATLAB для решения задачи линейной упругой контактной механики под названием «Решение LCP задачи линейной упругой контактной механики» представлена на файлообменнике MATLAB Central.
- [2]: Калькулятор контактной механики.
- [3]: подробные расчеты и формулы теории Дж. К. Реннера для двух сфер.
- [5]: Код Matlab для анализа контактов Герца (включая линейные, точечные и эллиптические случаи).
- [6]: Модели адгезии JKR, MD и DMT (процедуры Matlab).










































![{\displaystyle M_{x}=\int _{S}y~q_{z}(x,y)~\mathrm {d} A~;~~M_{y}=\int _{S}-x~ q_{z}(x,y)~\mathrm {d} A~;~~M_{z}=\int _{S}[x~q_{y}(x,y)-y~q_{x}(x,y)]~\mathrm {d} A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84858a589cb089aa631e81fb379d152b42ab368b)







![{\displaystyle {\begin{aligned}\sigma _{xx}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(xx'\right)^{2}\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{3}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(xx'\right)\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/748f49fbb04908de77b05ca997ec1baefdc73491)


![{\displaystyle {\begin{aligned}\sigma _{xx}&=-{\frac {2}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(xx'\right)^{3}\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(xx'\right)\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(xx'\right)^{2}\,dx'}{\left[\left(xx'\right)^{2}+z^{2}\right]^{2}}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3d99b5917ad56c9a691709199164f1bd9018c3f)












































![{\displaystyle {\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0,398942280401,0,159773702775,0,0389687688311,0,00364356495452]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=\left[1,653807476138,1,170419428529,0,448892964428,0,0951971709160,0,00931642803836,-6,383774657279\times 10^{-6}\right]\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91be480fb30f0f102dd6f2af32e97c2f0ba7a8a7)


![{\displaystyle {\begin{align}[][a_{0},a_{1},a_{2},a_{3}]&=[0,430019993662,0,101979509447,0,0229040629580,0,000688602924]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1,671117125984,1,199586555505,0,46936532151,0,102632881122,0,010686348714,0,0000517200271]\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b60e034e36c4936d8cb548ca96d555a463be8ce)






















![{\displaystyle {\begin{align}[][a_{0},a_{1},a_{2},a_{3}]&=[0,5,0,182536384941,0,039812283118,0,003684879001]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1,960841785003,1,708677456715,0,856592986083,0,264996791567,0,049257843893,0,004640740133]\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f29ff10822d1d70c853baeacd29de26639ec0413)


![{\displaystyle {\begin{align}[][a_{0},a_{1},a_{2},a_{3}]&=[0,616634218997,0,108855827811,0,023453835635,0,000449332509]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1,919948267476,1,635304362591,0,799392556572,0,240278859212,0,043178653945,0,003863334276]\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba5350391adf41af8360811b035ddd8bfd6670a)

![{\displaystyle F(z)={\cfrac {16\gamma}{3z_{0}}}\left[\left({\cfrac {z}{z_{0}}}\right)^{-9}-\left({\cfrac {z}{z_{0}}}\right)^{-3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cc0d0f528d67748519b18d1879f1294c69ad04f)


![{\displaystyle F_{a}(z)={\cfrac {16\gamma \pi R}{3}}\left[{\cfrac {1}{4}}\left({\cfrac {z}{z_{0}}}\right)^{-8}-\left({\cfrac {z}{z_{0}}}\right)^{-2}\right]~;~~{\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed6e557a37cc80e1cabcee94c45c1ed372b1afd)






























![{\displaystyle \mu :={\frac {d_{c}}{z_{0}}}\approx \left[{\frac {R(\Delta \gamma )^{2}}{{E^{*}}^{2}z_{0}^{3}}}\right]^{\frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee629f48f3b4619f743181ab1f51a37a65b6663)

















![{\displaystyle u^{H}(c)={\cfrac {1}{\pi R}}\left[a^{2}\left(2-m^{2}\right)\sin ^{-1}\left({\frac {1}{m}}\right)+a^{2}{\sqrt {m^{2}-1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc8fcd224f3cc8f0b4c13688f18599f477857de)

![{\displaystyle p^{D}(r)={\begin{cases}-{\frac {\sigma _{0}}{\pi }}\cos ^{-1}\left[{\frac {2-m^{2}-{\frac {r^{2}}{a^{2}}}}{m^{2}\left(1-{\frac {r^{2}}{m^{2}a^{2}}}\right)}}\right]&\quad {\text{for}}\quad r\leq a\\-\sigma _{0}&\quad {\text{for}}\quad a\leq r\leq c\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd9f07dae34286f3e0a287add88884474ed78b83)
![{\displaystyle F^{D}=-2\sigma _{0}m^{2}a^{2}\left[\cos ^{-1}\left({\frac {1}{m}}\right)+{\frac {1}{m^{2}}}{\sqrt {m^{2}-1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/627849d1b6250dce2090a9098d8227ad0f8e4d10)

![{\displaystyle h^{D}(c)=\left({\frac {4\sigma _{0}a}{\pi E^{*}}}\right)\left[{\sqrt {m^{2}-1}}\cos ^{-1}\left({\frac {1}{m}}\right)+1-m\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0313721de708f08ab70365bbafeba470b275a5f5)









![{\displaystyle {\bar {F}}={\bar {a}}^{3}-\lambda {\bar {a}}^{2}\left[{\sqrt {m^{2}-1}}+m^{2}\sec ^{-1}m\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e81925aa29d61950849b8ff97628db1fe9e869e)

![{\displaystyle {\frac {\lambda {\bar {a}}^{2}}{2}}\left[\left(m^{2}-2\right)\сек ^{-1}m+{\sqrt {m^{2}-1}}\right]+{\frac {4\lambda {\bar {a}}}{3}}\left[{\sqrt {m^{2}-1}}\сек ^{-1}m-m+1\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5628cdc5b5275a8e83a3589da8db3b2fdc10869d)









