Гемитессеракт

Гемитессеракт
(геми-4-куб)
Гемитессеракт ; (геми-4-куб)
Тип	Правильный проективный 4-мерный многогранник
Символ Шлефли	{4,3,3}/2 или {4,3,3} 4
Клетки	4 {4,3}
Лица	12 {4}
Края	16
Вершины	8
Вершинная фигура	Тетраэдр
Петри полигон	Квадрат
Двойной	геми-16-клеточный

Абстрактный правильный 4-мерный многогранник с 4 кубическими ячейками

В абстрактной геометрии полутессеракт — это абстрактный правильный 4-мерный многогранник , содержащий половину ячеек тессеракта , существующий в реальном проективном пространстве RP 3 ^. [ ^1]

Реализация

Он имеет четыре кубические ячейки, 12 квадратных граней, 16 ребер и 8 вершин. Он обладает неожиданным свойством, что каждая ячейка контактирует с каждой другой ячейкой на двух гранях, и каждая ячейка содержит все вершины, что дает пример абстрактного многогранника, грани которого не определяются их наборами вершин.


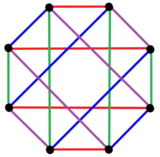В кубической проекции 4 кубические ячейки можно увидеть, выбрав 3 из 4 наборов параллельных ребер. Один прямой, а три видны как перекрестные кубы. Одна из 6 квадратных граней показана желтым в каждом кубе.	Проекция внутри правильного восьмиугольника с двумя цветами вершин, показывающая его как полный двудольный граф K _4,4 и его 4 набора по 4 параллельных ребра.

В виде графика

С точки зрения теории графов скелет представляет собой кубический граф с добавленными 8 диагональными центральными ребрами.

Это также полный двудольный граф K _4,4 и правильный комплексный многоугольник ₂ {4} ₄ , обобщенный крестообразный многогранник . ^{[ необходимо разъяснение ]}

Как конфигурация

Эта матрица конфигурации представляет собой полутессеракт. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем полутессеракте. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. ^[2] Например, 2 в первом столбце второй строки указывает, что в каждом ребре (т. е. на его крайних точках) имеется 2 вершины; 4 во втором столбце первой строки указывает, что в каждой вершине сходятся 4 ребра.

${\begin{bmatrix}{\begin{matrix}8&4&6&4\\2&16&3&3\\4&4&12&2\\8&12&6&4\end{matrix}}\end{bmatrix}}$

Смотрите также

Гемикуб (геометрия)

Ссылки

^ МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), «6C. Проективные правильные многогранники», Абстрактные правильные многогранники (1-е изд.), Cambridge University Press, стр. 162–165, ISBN 0-521-81496-0
^ Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Довер. стр. 12, §1.8 Конфигурации.

Внешние ссылки

Гемитессеракт
{4,3,3}4, эльтес, полутессеракт
Малая группа(192,955)

[1] МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), «6C. Проективные правильные многогранники», Абстрактные правильные многогранники (1-е изд.), Cambridge University Press, стр. 162–165, ISBN 0-521-81496-0

[2] Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Довер. стр. 12, §1.8 Конфигурации.