График дружбы
Граф треугольников с общей вершиной
График дружбы
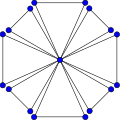Граф дружбы F 8 .
Вершины2 н + 1
Края3 н
Радиус1
Диаметр2
Обхват3
Хроматическое число3
Хроматический индекс2 н
Характеристики
ОбозначениеФ н
Таблица графиков и параметров
Графы дружбы F 2 , F 3 и F 4 .

В математической области теории графов граф дружбы (или граф голландской ветряной мельницы или n -веер ) F n представляет собой плоский неориентированный граф с 2 n + 1 вершинами и 3 n ребрами. [1]

Граф дружбы F n может быть построен путем соединения n копий графа-цикла C 3 с общей вершиной, которая становится универсальной вершиной для графа. [2]

По построению граф дружбы F n изоморфен графу ветряной мельницы Wd(3, n ) . Это единичное расстояние с обхватом 3, диаметром 2 и радиусом 1. Граф F 2 изоморфен графу бабочки . Графы дружбы обобщаются треугольными графами кактусов .

Теорема о дружбе

Теорема о дружбе Пола Эрдёша , Альфреда Реньи и Веры Т. Шош  (1966) [3] утверждает, что конечные графы со свойством, что каждые две вершины имеют ровно одного общего соседа, являются в точности графами дружбы. Неформально, если группа людей обладает свойством, что каждая пара людей имеет ровно одного общего друга, то должен быть один человек, который является другом всех остальных. Однако для бесконечных графов может быть много различных графов с той же мощностью, которые обладают этим свойством. [4]

Комбинаторное доказательство теоремы о дружбе было дано Мерциосом и Унгером. [5] Другое доказательство было дано Крейгом Хунеке. [6] Формализованное доказательство в Metamath было сообщено Александром ван дер Векенсом в октябре 2018 года в списке рассылки Metamath. [7]

Маркировка и окраска

Граф дружбы имеет хроматическое число 3 и хроматический индекс 2 n . Его хроматический многочлен может быть выведен из хроматического многочлена графа цикла C 3 и равен

( х − 2 ) н ( х − 1 ) н х {\displaystyle (x-2)^{n}(x-1)^{n}x} .

Граф дружбы F n является рёберно-грациозным тогда и только тогда, когда n нечётно. Он является грациозным тогда и только тогда, когда n ≡ 0 (mod 4) или n ≡ 1 (mod 4) . [8] [9]

Каждый граф дружбы является факторно-критическим .

Теория экстремальных графов

Согласно экстремальной теории графов , каждый граф с достаточным количеством ребер (относительно числа его вершин) должен содержать -веер в качестве подграфа. Более конкретно, это верно для -вершинного графа, если число ребер равно к {\displaystyle к} н {\displaystyle n}

⌊ н 2 4 ⌋ + ф ( к ) , {\displaystyle \left\lfloor {\frac {n^{2}}{4}}\right\rfloor +f(k),}

где is , если нечетно, и is , если четно. Эти оценки обобщают теорему Турана о числе ребер в графе без треугольников , и они являются наилучшими возможными оценками для этой задачи, поскольку для любого меньшего числа ребер существуют графы, которые не содержат -веер . [10] ф ( к ) {\displaystyle f(k)} к 2 − к {\displaystyle к^{2}-к} к {\displaystyle к} ф ( к ) {\displaystyle f(k)} к 2 − 3 к / 2 {\displaystyle к^{2}-3к/2} к {\displaystyle к} к {\displaystyle к}

Обобщения

Любые две вершины, имеющие ровно одного общего соседа, эквивалентны любым двум вершинам, соединенным ровно одним путем длины два. Это было обобщено на -графы, в которых любые две вершины соединены единственным путем длины . Поскольку такие графы неизвестны, и утверждение об их несуществовании является гипотезой Коцига . П к {\displaystyle P_{k}} к {\displaystyle к} к ≥ 3 {\displaystyle k\geq 3}

Смотрите также

  • Центральный орграф — ориентированный граф, обладающий свойством, что каждые две вершины могут быть соединены единственным двуребровым маршрутом.

Ссылки

  1. ^ Вайсштейн, Эрик В. , «Голландский график ветряных мельниц», MathWorld
  2. ^ Галлиан, Джозеф А. (3 января 2007 г.), «Динамический обзор маркировки графов», Электронный журнал комбинаторики : DS6, doi : 10.37236/27.
  3. ^ Эрдеш, Пол ; Реньи, Альфред ; Сос, Вера Т. (1966), «Об одной задаче теории графов» (PDF) , Studia Sci. Математика. Венгрия. , 1 : 215–235.
  4. ^ Chvátal, Václav ; Kotzig, Anton ; Rosenberg, Ivo G.; Davies, Roy O. (1976), «Существуют графы дружбы кардинального числа », Canadian Mathematical Bulletin , 19 (4): 431–433, doi : 10.4153/cmb-1976-064-1 2 ℵ α {\displaystyle \scriptstyle 2^{\aleph _{\alpha }}} ℵ α {\displaystyle \scriptstyle \aleph _{\alpha }} .
  5. ^ Мерциос, Джордж; Уолтер Унгер (2008), «Проблема дружбы на графах» (PDF) , Отношения, порядки и графы: взаимодействие с компьютерной наукой
  6. ↑ Huneke, Craig (1 января 2002 г.), «Теорема о дружбе», The American Mathematical Monthly , 109 (2): 192–194, doi :10.2307/2695332, JSTOR  2695332
  7. ^ ван дер Векенс, Александр (11 октября 2018 г.), «Теорема о дружбе (№ 83 из «списка 100 теорем»)», список рассылки Metamath
  8. ^ Бермонд, Ж.-К.; Брауэр, AE ; Джерма, А. (1978), «Системы триплетов и ассоциированные различия», Problèmes Combinatoires et Théorie des Graphes (Univ. Orsay, 1976) , Colloq. Стажер. дю CNRS, том. 260, CNRS, Париж, стр. 35–38, MR  0539936..
  9. ^ Bermond, J.-C.; Kotzig, A .; Turgeon, J. (1978), "О комбинаторной проблеме антенн в радиоастрономии", Combinatorics (Proc. Fifth hungary colloq., Keszthely, 1976), Vol. I , Colloq. Math. Soc. János Bolyai, vol. 18, North-Holland, Amsterdam-New York, стр. 135–149, MR  0519261.
  10. ^ Эрдёш, П.; Фюреди , З .; Гулд, Р. Дж .; Гундерсон, Д. С. (1995), «Экстремальные графы для пересекающихся треугольников», Журнал комбинаторной теории , Серия B, 64 (1): 89–100, CiteSeerX 10.1.1.491.974 , doi : 10.1006/jctb.1995.1026 , MR  1328293 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Friendship_graph&oldid=1252280394"