Факторно-критический граф
В теории графов , математической дисциплине, факторно-критический граф (или гипосопоставимый граф [1] [2] ) — это граф с n вершинами, в котором каждый индуцированный подграф из n − 1 вершин имеет совершенное паросочетание . (Совершенное паросочетание в графе — это подмножество его ребер со свойством, что каждая из его вершин является конечной точкой ровно одного из ребер в подмножестве.)
Паросочетание, которое охватывает все вершины графа, кроме одной, называется почти идеальным паросочетанием . Таким образом, эквивалентно, факторно-критический граф — это граф, в котором существуют почти идеальные паросочетания, которые избегают всех возможных вершин.
Примеры


Любой граф цикла нечетной длины является факторно-критическим, [1] как и любой полный граф с нечетным числом вершин. [3] В более общем смысле, любой гамильтонов граф с нечетным числом вершин является факторно-критическим. Графы дружбы (графы, образованные путем соединения набора треугольников в одной общей вершине) дают примеры графов, которые являются факторно-критическими, но не гамильтоновыми.
Если граф G является факторно-критическим, то таковым является и Мыцельскиан графа G. Например, граф Грётша , Мыцельскиан пятивершинного графа-цикла, является факторно-критическим. [4]
Каждый 2-вершинно-связный граф без клешней с нечетным числом вершин является факторно-критическим. Например, 11-вершинный граф, образованный путем удаления вершины из правильного икосаэдра (графа гироудлиненной пятиугольной пирамиды ), является как 2-связным, так и без клешней, поэтому он является факторно-критическим. Этот результат напрямую следует из более фундаментальной теоремы о том, что каждый связный граф без клешней с четным числом вершин имеет идеальное паросочетание. [5]
Характеристика
Факторно-критические графы можно охарактеризовать несколькими различными способами, помимо их определения как графов, в которых каждое удаление вершины допускает идеальное паросочетание:
- Тибор Галлаи доказал, что граф является факторно-критическим тогда и только тогда, когда он связен и для каждого узла v графа существует максимальное паросочетание , которое не включает v . Из этих свойств следует, что граф должен иметь нечетное число вершин и что каждое максимальное паросочетание должно соответствовать всем вершинам, кроме одной. [6]
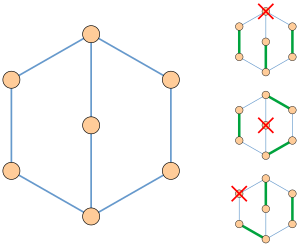
- Ласло Ловас доказал, что граф является факторно-критическим тогда и только тогда, когда он имеет нечетное разложение ушей , разбиение его ребер на последовательность подграфов, каждый из которых является путем или циклом нечетной длины , причем первый в последовательности является циклом, каждый путь в последовательности имеет обе конечные точки, но не имеет внутренних точек на вершинах в предыдущих подграфах, и каждый цикл, кроме первого в последовательности, имеет ровно одну вершину в предыдущих подграфах. Например, граф на иллюстрации может быть разделен таким образом на цикл из пяти ребер и путь из трех ребер. В случае, если также дано почти идеальное соответствие факторно-критического графа, разложение ушей может быть выбрано таким образом, что каждое ухо чередуется между согласованными и несогласованными ребрами. [7] [8]
- Граф также является факторно-критическим тогда и только тогда, когда его можно свести к одной вершине последовательностью сокращений циклов нечетной длины. Более того, в этой характеристике можно выбрать каждый цикл в последовательности так, чтобы он содержал вершину, образованную сокращением предыдущего цикла. [1] Например, если сжать уши разложения уха в порядке, заданном разложением, то в момент сжатия каждого уха он образует нечетный цикл, поэтому характеристику разложения уха можно использовать для нахождения последовательности нечетных циклов для сжатия. Наоборот, из последовательности сокращений нечетных циклов, каждое из которых содержит вершину, образованную предыдущим сокращением, можно сформировать разложение уха, в котором уши являются наборами ребер, сжатых на каждом шаге.
- Предположим, что граф G задан вместе с выбором вершины v и паросочетанием M , которое покрывает все вершины, кроме v . Тогда G является факторно-критическим тогда и только тогда, когда существует набор путей в G , чередующихся между сопоставленными и не сопоставленными ребрами, которые соединяют v с каждой из других вершин в G. Основываясь на этом свойстве, можно определить за линейное время , является ли граф G с заданным почти идеальным паросочетанием факторно-критическим. [9]
Характеристики
Факторно-критические графы всегда должны иметь нечетное число вершин и должны быть 2-ребристо-связанными (то есть они не могут иметь никаких мостов ). [10] Однако они не обязательно 2-вершинно-связаны ; графы дружбы дают контрпример. Факторно-критический граф не может быть двудольным , потому что в двудольном графе с почти идеальным паросочетанием единственные вершины, которые можно удалить, чтобы получить идеально паросочетаемый граф, — это вершины на большей стороне двудольного разбиения.
Каждый 2-вершинно-связанный факторно-критический граф с m ребрами имеет по крайней мере m различных почти совершенных паросочетаний, и в более общем случае каждый факторно-критический граф с m ребрами и c блоками (2-вершинно-связанные компоненты) имеет по крайней мере m − c + 1 различных почти совершенных паросочетаний. Графы, для которых эти границы узки, могут быть охарактеризованы наличием нечетных ушных разложений определенной формы. [3]
Любой связный граф может быть преобразован в факторно-критический граф путем сжатия достаточного количества его ребер. Минимальные наборы ребер, которые необходимо сжать, чтобы сделать заданный граф G факторно-критическим, образуют основания матроида , факт, который подразумевает, что жадный алгоритм может быть использован для нахождения минимального веса набора ребер, которые нужно сжать, чтобы сделать граф факторно-критическим, за полиномиальное время . [11]
Приложения
Цветок — это факторно-критический подграф большего графа. Цветки играют ключевую роль в алгоритмах Джека Эдмондса для максимального соответствия и минимального веса идеального соответствия в недвудольных графах. [12 ]
В полиэдральной комбинаторике факторно-критические графы играют важную роль в описании граней соответствующего многогранника данного графа. [1] [2]
Обобщения и связанные с ними концепции
Граф называется k -факторно-критическим, если каждое подмножество из n − k вершин имеет идеальное паросочетание. Согласно этому определению, гипосочетаемый граф является 1-факторно-критическим. [13] Еще более обще, граф является ( a , b ) -факторно-критическим, если каждое подмножество из n − k вершин имеет r -фактор, то есть является множеством вершин r -регулярного подграфа данного графа.
Критический граф ( без оговорок) обычно подразумевает граф, для которого удаление каждой из его вершин уменьшает количество цветов, необходимых для раскраски графа . Понятие критичности использовалось в теории графов гораздо более широко для обозначения графов, для которых удаление каждой возможной вершины изменяет или не изменяет некоторое соответствующее свойство графа. Граф, критический по соответствию, — это граф, для которого удаление любой вершины не изменяет размер максимального паросочетания ; по характеристике Галлаи, графы, критические по соответствию, — это в точности графы, в которых каждый связный компонент является факторно-критическим. [14] Дополнительный граф критического графа обязательно является критическим по соответствию, факт, который был использован Галлаи для доказательства нижних границ числа вершин в критическом графе. [15]
Помимо теории графов, концепция факторной критичности была распространена на матроиды путем определения типа разложения ушей на матроидах и определения матроида как факторно-критического, если он имеет разложение ушей, в котором все уши нечетные. [16]
Ссылки
- ^ abcd Pulleyblank, WR ; Edmonds, J. (1974), "Facets of 1-matching polyhedras", в Berge, C. ; Ray-Chaudhuri, DK (ред.), Hypergraph Seminar , Lecture Notes in Mathematics, т. 411, Springer-Verlag, стр. 214–242, doi :10.1007/BFb0066196, ISBN 978-3-540-06846-4.
- ^ ab Cornuéjols, G. ; Pulleyblank, WR (1983), «Критические графы, соответствия и туры или иерархия релаксаций для задачи коммивояжера», Combinatorica , 3 (1): 35–52, doi :10.1007/BF02579340, MR 0716420, S2CID 35825797.
- ^ ab Liu, Yan; Hao, Jianxiu (2002), «Перечисление почти идеальных паросочетаний факторно-критических графов», Discrete Mathematics , 243 (1–3): 259–266, doi :10.1016/S0012-365X(01)00204-7, MR 1874747.
- ^ Дошлич, Томислав (2005), «Мычельскианы и соответствия», Discussiones Mathematicae Graph Theory , 25 (3): 261–266, doi : 10.7151/dmgt.1279 , MR 2232992.
- ^ Favaron, Odile ; Flandrin, Evelyne ; Ryjáček, Zdeněk (1997), "Factor-criticality and matching extension in DCT-graphs", Discussiones Mathematicae Graph Theory , 17 (2): 271–278, CiteSeerX 10.1.1.25.6314 , doi :10.7151/dmgt.1054, MR 1627955 .
- ^ Галлай, Т. (1963), "Neuer Beweis eines Tutte'schen Satzes", Magyar Tud. Акад. Мат. Кутато Междунар. Кёзл. , 8 : 135–139, МР 0166777. По словам Франка Андраша ; Сегё, Ласло (2002), «Примечание к формуле сопоставления путей» (PDF) , Journal of Graph Theory , 41 (2): 110–119, CiteSeerX 10.1.1.20.7918 , doi : 10.1002/jgt.10055, MR 1926313, S2CID 206076722 .
- ^ Ловас, Л. (1972), «Заметка о факторно-критических графах», Studia Sci. Математика. Венгрия. , 7 : 279–280, МР 0335371.
- ^ Корте, Бернхард Х.; Виген, Йенс (2008), «10.4 Ушные разложения факторно-критических графов», Комбинаторная оптимизация: теория и алгоритмы, Алгоритмы и комбинаторика, т. 21 (4-е изд.), Springer-Verlag, стр. 235–241, ISBN 978-3-540-71843-7.
- ^ Лу, Динцзюнь; Рао, Доннинг (2004), «Характеристика критических графов факторов и алгоритм» (PDF) , The Australasian Journal of Combinatorics , 30 : 51–56, MR 2080453.
- ^ Сейфарт, Карен (1993), «Упаковки и совершенные двойные покрытия путей максимальных планарных графов», Дискретная математика , 117 (1–3): 183–195, doi : 10.1016/0012-365X(93)90334-P , MR 1226141.
- ^ Szigeti, Zoltán (1996), «О матроиде, определяемом ушными разложениями графов», Combinatorica , 16 (2): 233–241, doi :10.1007/BF01844849, MR 1401896, S2CID 206806006. Более ранний алгоритм для сокращения минимального числа (невзвешенных) ребер для достижения факторно-критического графа см. в Frank, András (1993), "Conservative weightings and ear-decompositions of graphs", Combinatorica , 13 (1): 65–81, doi :10.1007/BF01202790, MR 1221177, S2CID 10857300.
- ^ Эдмондс, Джек (1965), «Пути, деревья и цветы», Канадский журнал математики , 17 : 449–467, doi : 10.4153/CJM-1965-045-4 , MR 0177907, S2CID 18909734.
- ^ Фаварон, Одиль (1996), «О критических по k-фактору графах», Discussiones Mathematicae Graph Theory , 16 (1): 41–51, doi : 10.7151/dmgt.1022 , MR 1429805.
- ^ Эрдёш, П.; Фюреди , З .; Гулд, Р. Дж .; Гундерсон, Д. С. (1995), «Экстремальные графы для пересекающихся треугольников», Журнал комбинаторной теории , Серия B, 64 (1): 89–100, doi : 10.1006/jctb.1995.1026 , MR 1328293.
- ^ Галлай, Т. (1963b), "Kritische Graphen II", Publ. Математика. Инст. Венгрия. акад. наук. , 8 : 373–395. Как цитируется в Stehlík, Matěj (2003), "Критические графы со связанными дополнениями", Journal of Combinatorial Theory , Series B, 89 (2): 189–194, doi :10.1016/S0095-8956(03)00069-8, MR 2017723.
- ^ Сегеди, Балаж ; Сегеди, Кристиан (2006), «Симплектические пространства и ухо-разложение матроидов», Combinatorica , 26 (3): 353–377, doi :10.1007/s00493-006-0020-3, MR 2246153, S2CID 11578490.