Фолиум Декарта
Алгебраическая кривая вида x³ + y³ – 3axy = 0
Лист Декарта (зеленый) с асимптотой (синий), когда а = 1 {\displaystyle а=1}

В геометрии лист Декарта (от латинского folium  — лист ; назван в честь Рене Декарта ) — алгебраическая кривая, определяемая неявным уравнением х 3 + у 3 − 3 а х у = 0. {\displaystyle x^{3}+y^{3}-3axy=0.}

История

Кривая была впервые предложена и изучена Рене Декартом в 1638 году. [1] Ее известность связана с инцидентом в развитии исчисления . Декарт бросил вызов Пьеру де Ферма, чтобы найти касательную к кривой в произвольной точке, поскольку Ферма недавно открыл метод нахождения касательных линий. Ферма легко решил эту задачу, чего Декарт сделать не смог. [2] С момента изобретения исчисления наклон касательной можно легко найти с помощью неявного дифференцирования . [3]

Графическое изображение кривой

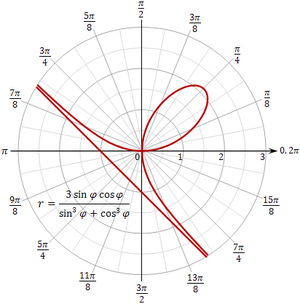
Лист Декарта в полярных координатах

Лист Декарта можно выразить в полярных координатах как, что изображено слева. Это эквивалентно [4] г = 3 а грех ⁡ θ потому что ⁡ θ грех 3 ⁡ θ + потому что 3 ⁡ θ , {\displaystyle r={\frac {3a\sin \theta \cos \theta }{\sin ^{3}\theta +\cos ^{3}\theta }},}

г = 3 а сек ⁡ θ загар ⁡ θ 1 + загар 3 ⁡ θ . {\displaystyle r={\frac {3a\сек \theta \tan \theta }{1+\tan ^{3}\theta }}.}

Другой метод заключается в том, чтобы записать и решить для и в терминах . Это дает рациональные параметрические уравнения : [5] у = п х {\displaystyle y=px} х {\displaystyle x} у {\displaystyle у} п {\displaystyle p}

х = 3 а п 1 + п 3 , у = 3 а п 2 1 + п 3 . {\displaystyle x={{3ap} \over {1+p^{3}}},\,y={{3ap^{2}} \over {1+p^{3}}}.}

Мы видим, что параметр связан с положением на кривой следующим образом:

  • п < − 1 {\displaystyle p<-1} соответствует , : правое, нижнее, «крыло». х > 0 {\displaystyle х>0} у < 0 {\displaystyle у<0}
  • − 1 < п < 0 {\displaystyle -1<p<0} соответствует , : левому, верхнему «крылу». х < 0 {\displaystyle х<0} у > 0 {\displaystyle у>0}
  • п > 0 {\displaystyle p>0} соответствует , : петле кривой. х > 0 {\displaystyle х>0} у > 0 {\displaystyle у>0}

Другой способ построения графика функции может быть получен из симметрии относительно . Симметрию можно увидеть непосредственно из ее уравнения (x и y можно поменять местами). Применив поворот на 45° по часовой стрелке, например, можно построить график функции, симметричный относительно повернутой оси x. у = х {\displaystyle у=х}

Эта операция эквивалентна замене: и дает Построение графика в декартовой системе дает лист, повернутый на 45° и, следовательно, симметричный относительно оси . х = ты + в 2 , у = ты − в 2 {\displaystyle x={{u+v} \over {\sqrt {2}}},\,y={{uv} \over {\sqrt {2}}}} в = ± ты 3 а 2 − 2 ты 6 ты + 3 а 2 . {\displaystyle v=\pm u{\sqrt {\frac {3a{\sqrt {2}}-2u}{6u+3a{\sqrt {2}}}}}.} ( ты , в ) {\displaystyle (u,v)} ты {\displaystyle u}

Характеристики

Она образует петлю в первом квадранте с двойной точкой в ​​начале координат и асимптотой Она симметрична относительно линии . Таким образом, они пересекаются в начале координат и в точке . х + у + а = 0 . {\displaystyle x+y+a=0\,.} у = х {\displaystyle у=х} ( 3 а / 2 , 3 а / 2 ) {\displaystyle (3a/2,3a/2)}

Неявное дифференцирование дает формулу для наклона касательной к этой кривой, которая будет [3] Используя любое из полярных представлений выше, площадь внутренней части петли оказывается равной . Более того, площадь между «крыльями» кривой и ее наклонной асимптотой также равна . [1] г у г х = а у − х 2 у 2 − а х . {\displaystyle {\frac {dy}{dx}}={\frac {ay-x^{2}}{y^{2}-ax}}.} 3 а 2 / 2 {\displaystyle 3a^{2}/2} 3 а 2 / 2 {\displaystyle 3a^{2}/2}

Связь с трисектрисой Маклорена

Трисектриса Маклорена

Лист Декарта связан с трисектрисой Маклорена аффинным преобразованием . Чтобы увидеть это, начните с уравнения и замените переменные, чтобы найти уравнение в системе координат, повернутой на 45 градусов. Это равносильно установке х 3 + у 3 = 3 а х у , {\displaystyle x^{3}+y^{3}=3axy\,,}

х = Х + И 2 , у = Х − И 2 . {\displaystyle x={{X+Y} \over {\sqrt {2}}},y={{XY} \over {\sqrt {2}}}.} В плоскости уравнение имеет вид Х , И {\displaystyle X,Y} 2 Х ( Х 2 + 3 И 2 ) = 3 2 а ( Х 2 − И 2 ) . {\displaystyle 2X(X^{2}+3Y^{2})=3{\sqrt {2}}a(X^{2}-Y^{2}).}

Если мы растянем кривую в направлении в раз, то получим уравнение , которое является уравнением трисектрисы Маклорена. И {\displaystyle Y} 3 {\displaystyle {\sqrt {3}}} 2 Х ( Х 2 + И 2 ) = а 2 ( 3 Х 2 − И 2 ) , {\displaystyle 2X(X^{2}+Y^{2})=a{\sqrt {2}}(3X^{2}-Y^{2}),}

Примечания

  1. ^ ab "Folium of Descartes". Энциклопедия математики . 5 июня 2020 г. Получено 30 января 2021 г.
  2. ^ Симмонс, стр. 101
  3. ^ ab Stewart, James (2012). "Раздел 3.5: Неявная дифференциация". Исчисление: Ранние трансцендентали . Соединенные Штаты Америки: Cengage Learning. стр. 209–11. ISBN 978-0-538-49790-9.
  4. ^ Стюарт, Джеймс (2012). "Глава 10: Параметрические уравнения и полярные координаты". Исчисление: Ранние трансцендентали (7-е изд.). Cengage Learning. стр. 687. ISBN 978-0-538-49790-9.
  5. ^ "DiffGeom3: Parametrized curves and algebraic curves". NJ Wildberger, University of New South Wales . Архивировано из оригинала 2021-12-21 . Получено 5 сентября 2013 г.

Ссылки

  • Дж. Деннис Лоуренс: Каталог специальных плоских кривых , 1972, Dover Publications. ISBN 0-486-60288-5 , стр. 106–108 
  • Джордж Ф. Симмонс : Исчисление драгоценностей: краткие жизни и памятные факты из математики , Нью-Йорк 1992, McGraw-Hill, xiv,355. ISBN 0-07-057566-5 ; новое издание 2007, Математическая ассоциация Америки ( MAA ) 
На Викискладе есть медиафайлы по теме «Фолиум Декарта» .
Взято с "https://en.wikipedia.org/w/index.php?title=Лист_Декарта&oldid=1217502602"