Синтез частотной модуляции
Форма звукового синтеза
Синтез FM с использованием 2 операторов
Несущий тон 220 Гц f c модулируется модулирующим тоном 440 Гц f m , с различными вариантами индекса частотной модуляции , β . Сигналы во временной области показаны выше, а соответствующие спектры показаны ниже (амплитуды спектра в дБ ).
Формы волн для каждого β

Спектры для каждого β

Синтез частотной модуляции (или синтез FM ) — это форма синтеза звука , при которой частота формы волны изменяется путем модуляции ее частоты с помощью модулятора. (Мгновенная) частота осциллятора изменяется в соответствии с амплитудой модулирующего сигнала. [1]

Синтез FM может создавать как гармонические, так и негармонические звуки. Для синтеза гармонических звуков модулирующий сигнал должен иметь гармоническую связь с исходным несущим сигналом. По мере увеличения количества частотной модуляции звук становится все более сложным. Благодаря использованию модуляторов с частотами, которые являются нецелыми кратными несущего сигнала (т. е. негармоническими), можно создавать негармонические колоколообразные и ударные спектры.

Синтез FM с использованием аналоговых генераторов может привести к нестабильности высоты тона. [2] Однако синтез FM также может быть реализован в цифровом виде, что более стабильно и стало стандартной практикой.

Приложения

В синтезаторах

Цифровой синтез FM (эквивалент фазовой модуляции с использованием временной интеграции мгновенной частоты ) был основой нескольких музыкальных инструментов, начиная с 1974 года. Yamaha построила первый прототип цифрового синтезатора в 1974 году, основанный на синтезе FM, [3] до коммерческого выпуска Yamaha GS-1 в 1980 году. [4] Synclavier I , производимый New England Digital Corporation с 1978 года, включал в себя цифровой синтезатор FM, использующий алгоритм синтеза FM, лицензированный у Yamaha. [5] Инновационный синтезатор Yamaha DX7 , выпущенный Yamaha в 1983 году, вывел FM на передний план синтеза в середине 1980-х годов. [6]

В ПК, игровых автоматах, игровых приставках и мобильных телефонах

Синтез FM также стал обычной настройкой для игр и программного обеспечения вплоть до середины девяностых. Звуковые карты для совместимых с IBM PC систем, такие как AdLib и Sound Blaster, популяризировали чипы Yamaha , такие как OPL2 и OPL3 . Другие компьютеры, такие как Sharp X68000 и MSX ( компьютерный блок Yamaha CX5M ), используют звуковой чип OPM (более поздние блоки CX5M используют звуковой чип OPP ). Компьютеры NEC PC-88 и PC-98 используют звуковые чипы OPN и OPNA .

Для аркадных систем и игровых консолей OPM использовался во многих аркадных платах 1980-х и 1990-х годов (включая аркадные платы System 16 от Sega и CP System от Capcom ); OPN также использовался в некоторых аркадных платах в 1980-х годах. OPNB в частности использовался в аркадных (MVS) и домашних консольных (AES) машинах SNK Neo Geo , а также использовался в качестве основного базового звукового генератора в аркадных платах Taito (вариант OPNB использовался в плате Taito Z System ). Родственный OPN2 использовался в Mega Drive (Genesis) от Sega , FM Towns Marty от Fujitsu и некоторых аркадных платах Sega (например, Sega System C-2 и Sega System 32) в качестве одного из чипов звукового генератора.

FM-синтез также использовался на широком спектре мобильных телефонов в 2000-х годах для воспроизведения рингтонов и других звуков с использованием формата Yamaha SMAF .

История

Дон Бухла (середина 1960-х)

Дон Бухла реализовал FM на своих инструментах в середине 1960-х годов, до патента Чоунинга. Его модули двойных осцилляторов 158, 258 и 259 имели специальный вход напряжения управления FM, [7] а модель 208 (Music Easel) имела жестко подключенный модуляционный осциллятор, позволяющий использовать как FM, так и AM первичного осциллятора. [8] Эти ранние приложения использовали аналоговые осцилляторы, и эта возможность также была подхвачена другими модульными синтезаторами и портативными синтезаторами, включая Minimoog и ARP Odyssey .

Джон Чоунинг (конец 1960-х – 1970-е годы)

Цифровой синтез частотной модуляции был разработан Джоном Чоунингом.

К середине 20-го века частотная модуляция (ЧМ), средство передачи звука, была понята в течение десятилетий и использовалась для трансляции радиопередач . ЧМ-синтез был разработан с 1967 года в Стэнфордском университете , Калифорния, Джоном Чоунингом , посредством его исследования цифрового синтеза и пространственного преобразования, вдохновленного новыми возможностями цифрового звука, описанными Максом Мэтьюзом [ нужна цитата ] . Его алгоритм [ нужна цитата ] был лицензирован японской компанией Yamaha в 1973 году . [3] Реализация, коммерциализированная Yamaha (патент США 4018121, апрель 1977 г. [9] или патент США 4,018,121 [10] ) , фактически основана на фазовой модуляции [ нужна цитата ] , но результаты в конечном итоге эквивалентны математически, поскольку оба по сути являются частным случаем квадратурной амплитудной модуляции [ нужна цитата ] . [11]

1970-е–1980-е годы

Расширения от Yamaha

Инженеры Yamaha начали адаптировать алгоритм Чоунинга для использования в коммерческом цифровом синтезаторе, добавив улучшения, такие как метод «масштабирования ключа», чтобы избежать введения искажений, которые обычно возникают в аналоговых системах во время частотной модуляции [ необходима ссылка ] , хотя прошло несколько лет, прежде чем Yamaha выпустила свои цифровые FM-синтезаторы. [12] В 1970-х годах Yamaha получила ряд патентов под прежним названием компании «Nippon Gakki Seizo Kabushiki Kaisha», развивая работу Чоунинга. [10] Yamaha построила первый прототип цифрового FM-синтезатора в 1974 году. [3] В конечном итоге Yamaha коммерциализировала технологию FM-синтеза с помощью Yamaha GS-1, первого цифрового FM-синтезатора, выпущенного в 1980 году. [4] FM-синтез был основой некоторых ранних поколений цифровых синтезаторов , в первую очередь от Yamaha, а также New England Digital Corporation по лицензии Yamaha. [5]

Цифровой синтезатор Yamaha DX7 FM (1983)

Синтезатор Yamaha DX7 , выпущенный в 1983 году, был вездесущим на протяжении 1980-х годов. Несколько других моделей Yamaha представили вариации и эволюции FM-синтеза в течение этого десятилетия. [13]

Yamaha запатентовала свою аппаратную реализацию FM в 1970-х годах [10], что позволило ей практически монополизировать рынок FM-технологий до середины 1990-х годов.

Casio разработала родственную форму синтеза, называемую синтезом фазовых искажений , которая использовалась в ее линейке синтезаторов CZ . Она имела похожее (но немного иное полученное) качество звука, что и серия DX.

1990-е

Бесплатное использование ФМ после истечения срока действия патента

С окончанием патента Стэнфордского университета на FM в 1995 году цифровой синтез FM теперь может свободно использоваться другими производителями. Патент на синтез FM принес Стэнфорду 20 миллионов долларов до истечения срока его действия, сделав его (в 1994 году) «вторым самым прибыльным лицензионным соглашением в истории Стэнфорда». [14]

Сегодня FM в основном встречается в программных синтезаторах, таких как Native Instruments ' FM8 или плагины Sytrus от Image-Line , но он также был включен в репертуар синтеза некоторых современных цифровых синтезаторов, обычно сосуществуя как опция вместе с другими методами синтеза, такими как субтрактивный , основанный на сэмплах синтез , аддитивный синтез и другие методы. Степень сложности FM в таких аппаратных синтезаторах может варьироваться от простого 2-операторного FM до очень гибких 6-операторных движков Korg Kronos и Alesis Fusion , до создания FM в широко модульных движках, таких как в последних синтезаторах Kurzweil Music Systems . [ требуется ссылка ]

Позднее использование FM и других технологий: свертка и модуляция в реальном времени (AFM + сэмпл) и синтез с формантным формированием

Синтезаторы Yamaha SY99 [15] и FS1R [16] позиционировали свои мощные возможности FM как аналоги синтеза на основе сэмплов и формантного синтеза соответственно. Новые аппаратные синтезаторы, специально предназначенные для своих возможностей FM, исчезли с рынка после выпуска FS1R в 1999 году, однако хорошо развитые возможности синтеза FM являются особенностью синтезаторов Nord Lead , производимых Clavia, линейки Alesis Fusion , Korg Oasys и Kronos и Modor NF-1. Различные другие синтезаторы предлагают ограниченные возможности FM в дополнение к своим основным двигателям. [ необходима цитата ]

FS1R имел 16 операторов, 8 стандартных операторов FM и 8 дополнительных операторов, которые использовали источник шума вместо осциллятора в качестве источника звука. Добавляя настраиваемые источники шума, FS1R мог моделировать звуки, производимые человеческим голосом и духовым инструментом, а также создавать звуки ударных инструментов. FS1R также содержал дополнительную волновую форму, называемую волновой формой форманты. Форманты можно использовать для моделирования резонирующих звуков корпусных инструментов, таких как виолончель, скрипка, акустическая гитара, фагот, английский рожок или человеческий голос. Форманты можно найти даже в гармоническом спектре нескольких медных духовых инструментов. [17]

2000-е годы–настоящее время

Дополнительные улучшения: переменная фазовая модуляция, синтез FM-X, измененная FM и т. д.

В 2016 году компания Korg выпустила Korg Volca FM — 3-голосную 6-операторную FM-версию серии компактных и доступных настольных модулей Korg Volca . [18] Компания Korg также выпустила opsix (2020) и opsix SE (2023), объединяющие 6-операторный FM-синтез с субтрактивным, аналоговым моделированием, аддитивным, полумодулярным и Waveshaping.

Yamaha выпустила Montage в 2016 году, который объединяет 128-голосный движок на основе сэмплов с 128-голосным движком FM. Эта итерация FM называется FM-X и включает 8 операторов; у каждого оператора есть выбор из нескольких основных форм волн, но у каждой формы волн есть несколько параметров для настройки ее спектра. [19] Затем в 2018 году последовал более доступный Yamaha MODX с 64-голосной архитектурой FM-X с 8 операторами в дополнение к 128-голосному движку на основе сэмплов. [20] MODX+, выпущенный в 2022 году, увеличил количество голосов движка FM-X до 128, как и в Montage. [21] В 2023 году Montage сменил Montage M, который использует тот же 128-голосный 8-операторный движок FM-X вместе с 128-голосным движком на основе сэмплов и недавно представленным 16-голосным 3-осцилляторным аналоговым движком, известным как AN-X. [22]

В 2018 году компания Elektron выпустила Digitone — 8-голосный 4-операторный FM-синтезатор с известным движком секвенсора Elektron. [23]

Синтез FM-X был впервые представлен в синтезаторах Yamaha Montage в 2016 году. FM-X использует 8 операторов. Каждый оператор FM-X имеет набор многоспектральных волновых форм на выбор, что означает, что каждый оператор FM-X может быть эквивалентен стеку из 3 или 4 FM-операторов DX7. Список выбираемых волновых форм включает синусоиды, волновые формы All1 и All2, волновые формы Odd1 и Odd2, а также волновые формы Res1 и Res2. Выбор синусоидальной волны работает так же, как и волновые формы DX7. Волновые формы All1 и All2 представляют собой пилообразную волновую форму. Волновые формы Odd1 и Odd2 представляют собой импульсные или прямоугольные волны. Эти два типа волновых форм можно использовать для моделирования основных гармонических пиков в нижней части гармонического спектра большинства инструментов. Волновые формы Res1 и Res2 перемещают спектральный пик к определенной гармонике и могут использоваться для моделирования либо треугольных, либо округлых групп гармоник дальше в спектре инструмента. Объединение волновой формы All1 или Odd1 с несколькими волновыми формами Res1 (или Res2) (и регулировка их амплитуд) может моделировать гармонический спектр инструмента или звука. [17] [ необходима цитата ]

Объединение наборов из 8 операторов FM с многоспектральными волновыми формами было впервые представлено в FS1R, выпущенном в 1999 году компанией Yamaha. Он смог достичь результатов, аналогичных результатам FM-X, используя 8 шумовых операторов.

Спектральный анализ

Демонстрация с 2 операторами: если частота модулятора ниже частоты несущей, выходная нота будет соответствовать частоте модулятора.

Существует множество разновидностей FM-синтеза, в том числе:

  • Различные операторские конфигурации (известные как «алгоритмы FM» в терминологии Yamaha)
    • 2 оператора
    • Последовательная FM (многоступенчатая)
    • Параллельная ЧМ (несколько модуляторов, несколько несущих),
    • Смесь из них
  • Различные формы волн операторов
    • Синусоидальная форма волны
    • Другие формы волн
  • Дополнительная модуляция

и т. д .

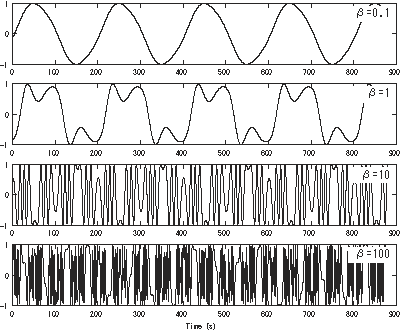
В качестве основы этих вариаций мы анализируем спектр 2-х операторов (линейный синтез ЧМ с использованием двух синусоидальных операторов) по следующему.

2 оператора

Спектр, генерируемый синтезом FM с одним модулятором, выражается следующим образом: [24] [25]

Для сигнала модуляции несущий сигнал равен: [примечание 1] м ( т ) = Б грех ⁡ ( ω м т ) {\displaystyle m(t)=B\,\sin(\omega _{m}t)\,}

Ф М ( т )   =   А грех ⁡ ( ∫ 0 т ( ω с + Б грех ⁡ ( ω м τ ) ) г τ )   =   А грех ⁡ ( ω с т − Б ω м ( потому что ⁡ ( ω м т ) − 1 ) )   =   А грех ⁡ ( ω с т + Б ω м ( грех ⁡ ( ω м т − π / 2 ) + 1 ) ) {\displaystyle {\begin{aligned}FM(t)&\ =\ A\,\sin \left(\,\int _{0}^{t}\left(\omega _{c}+B\,\sin(\omega _{m}\,\tau )\right)d\tau \right)\\&\ =\ A\,\sin \left(\omega _{c}\,t-{\frac {B}{\omega _{m}}}\left(\cos(\omega _{m}\,t)-1\right)\right)\\&\ =\ A\,\sin \left(\omega _{c}\,t+{\frac {B}{\omega _{m}}}\left(\sin(\omega _{m}\,t-\pi /2)+1\right)\right)\\\end{align}}}

Если бы мы проигнорировали постоянные фазовые члены на несущей и модуляторе , в конечном итоге мы получили бы следующее выражение, как показано в Chowning 1973 и Roads 1996, стр. 232: ϕ с = Б / ω м {\displaystyle \phi _{c}=B/\omega _{m}\,} ϕ м = − π / 2 {\displaystyle \phi _{m}=-\pi /2\,}

Ф М ( т )   ≈   А грех ⁡ ( ω с т + β грех ⁡ ( ω м т ) )   =   А ( Дж. 0 ( β ) грех ⁡ ( ω с т ) + ∑ н = 1 ∞ Дж. н ( β ) [ грех ⁡ ( ( ω с + н ω м ) т )   +   ( − 1 ) н грех ⁡ ( ( ω с − н ω м ) т ) ] )   =   А ∑ н = − ∞ ∞ Дж. н ( β ) грех ⁡ ( ( ω с + н ω м ) т ) {\displaystyle {\begin{aligned}FM(t)&\ \approx \ A\,\sin \left(\omega _{c}\,t+\beta \,\sin(\omega _{m}\,t)\right)\\&\ =\ A\left(J_{0}(\beta )\sin(\omega _{c}\,t)+\sum _{n=1}^{\infty }J_{n}(\beta )\left[\,\sin((\omega _{c}+n\,\omega _{m})\,t)\ +\ (-1)^{n}\sin((\omega _{c}-n\,\omega _{m})\,t)\,\right]\right)\\&\ =\ A\sum _{n=-\infty }^{\infty }J_{n}(\beta )\,\sin((\omega _{c}+n\,\omega _{m})\,t)\end{align}}}

где - угловые частоты ( ) несущей и модулятора, - индекс частотной модуляции , а амплитуды - -ая функция Бесселя первого рода , соответственно. [примечание 2] ω с , ω м {\displaystyle \omega _{c}\,,\,\omega _{m}\,} ω = 2 π ф {\displaystyle \,\omega =2\pi f\,} β = Б / ω м {\displaystyle \beta =B/\omega _{m}\,} Дж. н ( β ) {\displaystyle J_{n}(\beta)\,} н {\displaystyle n\,}

Смотрите также

Ссылки

Сноски

  1. ^ Обратите внимание, что сигнал модуляции, как мгновенная частота, преобразуется в фазу несущего сигнала посредством интеграла по времени между . м ( т ) {\displaystyle m(t)} Ф М ( т ) {\displaystyle FM(т)} [ 0 , т ] {\displaystyle [0,т]}
  2. ^ Выражение выше преобразуется с использованием формул тригонометрического сложения.
    грех ⁡ ( х ± у ) = грех ⁡ х потому что ⁡ у ± потому что ⁡ х грех ⁡ у {\displaystyle {\begin{aligned}\sin(x\pm y) &=\sin x\cos y\pm \cos x\sin y\end{aligned}}}
    и лемма о функции Бесселя
    потому что ⁡ ( β грех ⁡ θ ) = Дж. 0 ( β ) + 2 ∑ н = 1 ∞ Дж. 2 н ( β ) потому что ⁡ ( 2 н θ ) грех ⁡ ( β грех ⁡ θ ) = 2 ∑ н = 0 ∞ Дж. 2 н + 1 ( β ) грех ⁡ ( ( 2 н + 1 ) θ ) {\displaystyle {\begin{align}\cos(\beta \sin \theta )&=J_{0}(\beta )+2\sum _{n=1}^{\infty }J_{2n}(\beta )\cos(2n\theta )\\\sin(\beta \sin \theta )&=2\sum _{n=0}^{\infty }J_{2n+1}(\beta )\sin((2n+1)\theta )\end{align}}}
    ( Источник : Крех 2012)
    следующим образом:
    грех ⁡ ( θ с + β грех ⁡ ( θ м ) )   =   грех ⁡ ( θ с ) потому что ⁡ ( β грех ⁡ ( θ м ) ) + потому что ⁡ ( θ с ) грех ⁡ ( β грех ⁡ ( θ м ) )   =   грех ⁡ ( θ с ) [ Дж. 0 ( β ) + 2 ∑ н = 1 ∞ Дж. 2 н ( β ) потому что ⁡ ( 2 н θ м ) ] + потому что ⁡ ( θ с ) [ 2 ∑ н = 0 ∞ Дж. 2 н + 1 ( β ) грех ⁡ ( ( 2 н + 1 ) θ м ) ]   =   Дж. 0 ( β ) грех ⁡ ( θ с ) + Дж. 1 ( β ) 2 потому что ⁡ ( θ с ) грех ⁡ ( θ м ) + Дж. 2 ( β ) 2 грех ⁡ ( θ с ) потому что ⁡ ( 2 θ м ) + Дж. 3 ( β ) 2 потому что ⁡ ( θ с ) грех ⁡ ( 3 θ м ) + . . .   =   Дж. 0 ( β ) грех ⁡ ( θ с ) + ∑ н = 1 ∞ Дж. н ( β ) [ грех ⁡ ( θ с + н θ м )   +   ( − 1 ) н грех ⁡ ( θ с − н θ м ) ]   =   ∑ н = − ∞ ∞ Дж. н ( β ) грех ⁡ ( θ с + н θ м ) ( ∵   Дж. − н ( х ) = ( − 1 ) н Дж. н ( х ) ) {\displaystyle {\begin{aligned}&\sin \left(\theta _{c}+\beta \,\sin(\theta _{m})\right)\\&\ =\ \sin(\theta _{c})\cos(\beta \sin(\theta _{m}))+\cos(\theta _{c})\sin(\beta \sin(\theta _{m}))\\&\ =\ \sin(\theta _{c})\left[J_{0}(\beta )+2\sum _{n=1}^{\infty }J_{2n}(\beta )\cos(2n\theta _{m})\right]+\cos(\theta _{c})\left[2\sum _{n=0}^{\infty }J_{2n+1}(\beta )\sin((2n+1)\theta _{m})\right]\\&\ =\ J_{0}(\beta )\sin(\theta _{c})+J_{1}(\beta )2\cos(\theta _{c})\sin(\theta _{m})+J_{2}(\beta )2\sin(\theta _{c})\cos(2\theta _{m})+J_{3}(\beta )2\cos(\theta _{c})\sin(3\theta _{m})+...\\&\ =\ J_{0}(\beta )\sin(\theta _{c})+\sum _{n=1}^{\infty }J_{n}(\beta )\left[\,\sin(\theta _{c}+n\theta _{m})\ +\ (-1)^{n}\sin(\theta _{c}-n\theta _{m})\,\right]\\&\ =\ \sum _{n=-\infty }^{\infty }J_{n}(\beta )\,\sin(\theta _{c}+n\theta _{m})\qquad (\because \ J_{-n}(x)=(-1)^{n}J_{n}(x))\end{aligned}}}

Цитаты

  1. ^ Додж и Джерс 1997, стр. 115
  2. ^ Макгуайр, Сэм; Матею, Збинек (28 декабря 2020 г.). Искусство цифровой оркестровки. ЦРК Пресс. ISBN 978-1-000-28699-1.
  3. ^ abc "[Глава 2] FM-генераторы тона и заря домашнего музыкального производства". Yamaha Synth 40th Anniversary - History . Yamaha Corporation. 2014. Архивировано из оригинала 2017-05-11.
  4. ^ ab Curtis Roads (1996). Учебник компьютерной музыки. MIT Press . стр. 226. ISBN 0-262-68082-3. Получено 2011-06-05 .
  5. ^ ab "1978 New England Digital Synclavier". Mix . Penton Media. 1 сентября 2006 г.
  6. ^ "10 лучших классических пресетов синтезатора (и где их можно услышать)". MusicRadar . Получено 19 октября 2018 г. .
  7. ^ Доктор Хьюберт Хоу (1960-е). Электронная музыкальная система Buchla: Руководство пользователя, написанное для музыкальных инструментов CBS (Руководство пользователя Buchla 100). Отдел образовательных исследований, музыкальные инструменты CBS, Columbia Broadcasting System. стр. 7. На этом этапе мы можем рассмотреть различные дополнительные модификации сигнала, которые мы, возможно, захотим внести в серию тонов, производимых в приведенном выше примере. Например, если мы хотим добавить частотную модуляцию к тонам, необходимо подключить другой аудиосигнал к разъему, соединенному линией со средним диском на двойном синусно-пилообразном генераторе модели 158. ...
  8. ^ Аттен Стрэндж (1974). Программирование и метапрограммирование в электроорганизме — операционная директива для музыкального мольберта. Buchla and Associates.
  9. ^ "Патент США 4018121, апрель 1977 г.". patft.uspto.gov . Получено 30 апреля 2017 г. .
  10. ^ abc "Патент US4018121 - Метод синтеза музыкального звука - Google Patents" . Получено 2017-04-30 .
  11. ^ Роб Хордейк. "FM-синтез на Modular". Советы и хитрости Nord Modular и Micro Modular V3.03 . Clavia DMI AB. Архивировано из оригинала 2007-04-07 . Получено 2013-03-23 .
  12. ^ Холмс, Том (2008). «Ранняя компьютерная музыка». Электронная и экспериментальная музыка: технологии, музыка и культура (3-е изд.). Тейлор и Фрэнсис . С.  257– 8. ISBN 978-0-415-95781-6. Получено 2011-06-04 .
  13. ^ Гордон Рид (сентябрь 2001 г.). "Звуки 80-х, часть 2: Yamaha DX1 и ее последователи (ретро)". Sound on Sound . Архивировано из оригинала 17 сентября 2011 г. Получено 29 июня 2011 г.
  14. ^ Stanford University News Service (06/07/94), Музыкальный синтез приближается к качеству звука реальных инструментов
  15. ^ "Yamaha SY99 spec". Корпорация Yamaha (на японском).
  16. ^ Пойзер, Дебби; Джонсон, Дерек (1998). "Yamaha FS1R - FM-синтез / формантный тон-генератор". Sound on Sound . № декабрь 1998 г.
  17. ^ ab Zollinger, W. Thor (декабрь 2017 г.). "FM_Synthesis_of_Real_Instruments" (PDF) . Архивировано (PDF) из оригинала 2017-09-25.
  18. ^ Страница продукта Volca FM
  19. ^ Страница характеристик продукции Yamaha Montage
  20. ^ Страница характеристик продукта Yamaha MODX
  21. ^ Функции MODX8+, MODX7+ и MODX6+
  22. ^ МОНТАЖ М Синтезатор
  23. ^ Страница продукта Digitone
  24. ↑ Чоунинг 1973, стр. 1–2.
  25. ^ Деринг, Эд. "Математика частотной модуляции" . Получено 11 апреля 2013 г.

Библиография

  • Чоунинг, Дж. (1973). "Синтез сложных звуковых спектров с помощью частотной модуляции" (PDF) . Журнал Audio Engineering Society . 21 (7).
  • Чоунинг, Джон; Бристоу, Дэвид (1986). Теория и применение FM - Музыканты для музыкантов . Токио: Yamaha. ISBN 4-636-17482-8.
  • Додж, Чарльз; Джерс, Томас А. (1997). Компьютерная музыка: синтез, композиция и исполнение . Нью-Йорк: Schirmer Books. ISBN 0-02-864682-7.
  • Крех, Мартин (2012), «Функции Бесселя» (PDF) , Университет штата Пенсильвания , стр. 5–6, архивировано из оригинала (PDF) 18.11.2017 , извлечено 22.08.2014
  • Roads, Curtis (1996). Учебник компьютерной музыки. MIT Press. ISBN 978-0-262-68082-0.
  • Введение в FM, Билл Шотштедт
  • FM-руководство
  • Секреты синтезатора, часть 12: Введение в частотную модуляцию, Гордон Рид
  • Секреты синтезатора, часть 13: Подробнее о частотной модуляции, Гордон Рид
  • Школа синтезатора Пола Виффенса: Часть 3
  • FM-синтез, включая комплексный операторный анализ, зеркальный сайт FM-синтеза, 2019
Retrieved from "https://en.wikipedia.org/w/index.php?title=Frequency_modulation_synthesis&oldid=1265506040"