Частотная модуляция
| Полосовая модуляция |
|---|
 |
| Аналоговая модуляция |
| Цифровая модуляция |
| Иерархическая модуляция |
| Расширенный спектр |
| Смотрите также |
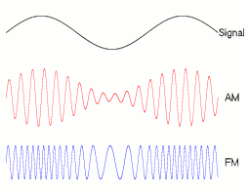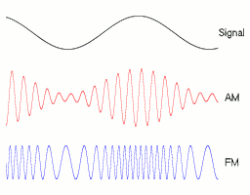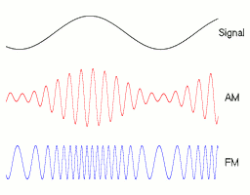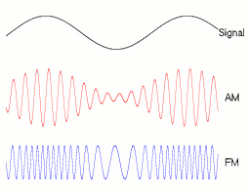

Частотная модуляция ( ЧМ ) — это кодирование информации в несущей волне путем изменения мгновенной частоты волны. Технология используется в телекоммуникациях , радиовещании , обработке сигналов и вычислительной технике .
При аналоговой частотной модуляции, например, в радиовещании, аудиосигнала, представляющего голос или музыку, мгновенное отклонение частоты , т. е. разница между частотой несущей и ее центральной частотой, имеет функциональную связь с амплитудой модулирующего сигнала.
Цифровые данные могут быть закодированы и переданы с помощью типа частотной модуляции, известной как частотная манипуляция (FSK), при которой мгновенная частота несущей смещается между набором частот. Частоты могут представлять цифры, такие как «0» и «1». FSK широко используется в компьютерных модемах , таких как факс-модемы , телефонных системах идентификации вызывающего абонента , открывателях гаражных ворот и других низкочастотных передачах. [1] Радиотелетайп также использует FSK. [2]
Частотная модуляция широко используется для радиовещания FM . Она также используется в телеметрии , радаре , сейсмической разведке и мониторинге новорожденных на предмет припадков с помощью ЭЭГ , [3] двусторонних радиосистемах , синтезе звука , системах записи на магнитную ленту и некоторых системах передачи видео. В радиопередаче преимущество частотной модуляции заключается в том, что она имеет большее отношение сигнал/шум и, следовательно, лучше подавляет радиочастотные помехи , чем сигнал амплитудной модуляции (АМ) равной мощности . По этой причине большая часть музыки транслируется по радио FM .
Однако в достаточно жестких условиях многолучевого распространения он работает намного хуже, чем AM, с отчетливыми высокочастотными шумовыми артефактами, которые слышны при более низкой громкости и менее сложных тонах. [ необходима цитата ] При достаточно высокой громкости и отклонении несущей начинают возникать искажения звука, которые в противном случае не присутствовали бы без многолучевого распространения или с AM-сигналом. [ необходима цитата ]
Частотная модуляция и фазовая модуляция являются двумя взаимодополняющими основными методами угловой модуляции ; фазовая модуляция часто используется как промежуточный шаг для достижения частотной модуляции. Эти методы контрастируют с амплитудной модуляцией , в которой амплитуда несущей волны изменяется, в то время как частота и фаза остаются постоянными.
Теория
This section needs additional citations for verification. (November 2017) |
Если передаваемая информация (т.е. сигнал основной полосы частот ) равна , а синусоидальная несущая равна , где f c — базовая частота несущей, а A c — амплитуда несущей, модулятор объединяет несущую с сигналом данных основной полосы частот, чтобы получить передаваемый сигнал: [4] [ необходима цитата ]
где , — чувствительность частотного модулятора, — амплитуда модулирующего сигнала или сигнала основной полосы частот.
В этом уравнении — мгновенная частота осциллятора, а — отклонение частоты , которое представляет собой максимальное смещение от f c в одном направлении, предполагая, что x m ( t ) ограничено диапазоном ±1.
Важно понимать, что этот процесс интегрирования мгновенной частоты для создания мгновенной фазы существенно отличается от того, что наивно подразумевает термин «частотная модуляция», а именно от прямого добавления модулирующего сигнала к несущей частоте.
что приведет к модулированному сигналу, имеющему ложные локальные минимумы и максимумы, не соответствующие таковым несущей.
Хотя большая часть энергии сигнала содержится в f c ± f Δ , можно показать с помощью анализа Фурье , что для точного представления сигнала FM требуется более широкий диапазон частот. Частотный спектр фактического сигнала FM имеет компоненты, простирающиеся бесконечно, хотя их амплитуда уменьшается, а компоненты более высокого порядка часто игнорируются в практических задачах проектирования. [5]
Синусоидальный сигнал основной полосы частот
Математически, модулирующий сигнал основной полосы частот может быть аппроксимирован синусоидальным непрерывным волновым сигналом с частотой f m . Этот метод также называется однотональной модуляцией. Интеграл такого сигнала равен:
В этом случае выражение для y(t) выше упрощается до:
где амплитуда модулирующей синусоиды представлена в пиковом отклонении (см. отклонение частоты ).
Гармоническое распределение несущей синусоидальной волны , модулированной таким синусоидальным сигналом, можно представить с помощью функций Бесселя ; это обеспечивает основу для математического понимания частотной модуляции в частотной области.
Индекс модуляции
Как и в других системах модуляции, индекс модуляции указывает, насколько модулированная переменная изменяется вокруг своего немодулированного уровня. Он относится к изменениям несущей частоты :
где - самая высокая частотная составляющая, присутствующая в модулирующем сигнале x m ( t ), а - пиковое отклонение частоты, т. е. максимальное отклонение мгновенной частоты от несущей частоты. Для синусоидальной модуляции индекс модуляции рассматривается как отношение пикового отклонения частоты несущей волны к частоте модулирующей синусоидальной волны.
Если , то модуляция называется узкополосной ЧМ (NFM), а ее полоса пропускания приблизительно равна . Иногда индекс модуляции считается NFM, а другие индексы модуляции считаются широкополосной ЧМ (WFM или FM).
Для систем цифровой модуляции, например, двоичной частотной манипуляции (BFSK), где двоичный сигнал модулирует несущую, индекс модуляции определяется по формуле:
где - период символа, и используется как наивысшая частота модулирующего двоичного сигнала по соглашению, хотя было бы точнее сказать, что это наивысшая основная частота модулирующего двоичного сигнала. В случае цифровой модуляции несущая никогда не передается. Вместо этого передается одна из двух частот, либо , либо , в зависимости от двоичного состояния 0 или 1 сигнала модуляции.
Если , модуляция называется широкополосной ЧМ , а ее полоса пропускания составляет приблизительно . Хотя широкополосная ЧМ использует большую полосу пропускания, она может значительно улучшить отношение сигнал/шум ; например, удвоение значения , при сохранении постоянного значения, приводит к восьмикратному улучшению отношения сигнал/шум. [6] (Сравните это с расширенным спектром ЛЧМ , который использует чрезвычайно широкие отклонения частоты для достижения выигрыша в обработке, сопоставимого с традиционными, более известными режимами расширенного спектра).
При тонально-модулированной волне FM, если частота модуляции остается постоянной, а индекс модуляции увеличивается, (не пренебрежимо малая) полоса пропускания сигнала FM увеличивается, но интервал между спектрами остается прежним; некоторые спектральные компоненты уменьшаются по силе, а другие увеличиваются. Если отклонение частоты сохраняется постоянным, а частота модуляции увеличивается, интервал между спектрами увеличивается.
Частотная модуляция может быть классифицирована как узкополосная, если изменение несущей частоты примерно такое же, как частота сигнала, или как широкополосная, если изменение несущей частоты намного выше (индекс модуляции > 1), чем частота сигнала. [7] Например, узкополосная FM (NFM) используется для систем двусторонней радиосвязи , таких как Family Radio Service , в которых несущая частота может отклоняться только на 2,5 кГц выше и ниже центральной частоты с речевыми сигналами с полосой пропускания не более 3,5 кГц. Широкополосная FM используется для FM-вещания , в котором музыка и речь передаются с отклонением до 75 кГц от центральной частоты и переносят аудио с полосой пропускания до 20 кГц и поднесущими до 92 кГц.
Функции Бесселя

Для случая несущей, модулированной одной синусоидальной волной, результирующий частотный спектр может быть рассчитан с использованием функций Бесселя первого рода, как функции номера боковой полосы и индекса модуляции. Амплитуды несущей и боковой полосы проиллюстрированы для различных индексов модуляции сигналов FM. Для определенных значений индекса модуляции амплитуда несущей становится равной нулю, и вся мощность сигнала находится в боковых полосах. [5]
Поскольку боковые полосы находятся по обе стороны несущей, их количество удваивается, а затем умножается на модулирующую частоту, чтобы найти ширину полосы пропускания. Например, девиация 3 кГц, модулированная аудиотоном 2,2 кГц, дает индекс модуляции 1,36. Предположим, что мы ограничимся только теми боковыми полосами, которые имеют относительную амплитуду не менее 0,01. Тогда, изучая диаграмму, мы увидим, что этот индекс модуляции даст три боковые полосы. Эти три боковые полосы, будучи удвоенными, дают нам (6 × 2,2 кГц) или требуемую полосу пропускания 13,2 кГц.
Индекс модуляции | Амплитуда боковой полосы | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Перевозчик | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 0.00 | 1.00 | ||||||||||||||||
| 0,25 | 0,98 | 0,12 | |||||||||||||||
| 0,5 | 0,94 | 0,24 | 0,03 | ||||||||||||||
| 1.0 | 0,77 | 0,44 | 0.11 | 0,02 | |||||||||||||
| 1.5 | 0,51 | 0,56 | 0,23 | 0,06 | 0,01 | ||||||||||||
| 2.0 | 0,22 | 0,58 | 0,35 | 0,13 | 0,03 | ||||||||||||
| 2.40483 | 0.00 | 0,52 | 0,43 | 0.20 | 0,06 | 0,02 | |||||||||||
| 2.5 | −0,05 | 0,50 | 0,45 | 0,22 | 0,07 | 0,02 | 0,01 | ||||||||||
| 3.0 | −0,26 | 0,34 | 0,49 | 0,31 | 0,13 | 0,04 | 0,01 | ||||||||||
| 4.0 | −0,40 | −0,07 | 0,36 | 0,43 | 0,28 | 0,13 | 0,05 | 0,02 | |||||||||
| 5.0 | −0,18 | −0,33 | 0,05 | 0,36 | 0,39 | 0,26 | 0,13 | 0,05 | 0,02 | ||||||||
| 5.52008 | 0.00 | −0,34 | −0,13 | 0,25 | 0,40 | 0,32 | 0,19 | 0,09 | 0,03 | 0,01 | |||||||
| 6.0 | 0,15 | −0,28 | −0,24 | 0.11 | 0,36 | 0,36 | 0,25 | 0,13 | 0,06 | 0,02 | |||||||
| 7.0 | 0.30 | 0.00 | −0,30 | −0,17 | 0,16 | 0,35 | 0,34 | 0,23 | 0,13 | 0,06 | 0,02 | ||||||
| 8.0 | 0,17 | 0,23 | −0,11 | −0,29 | −0,10 | 0,19 | 0,34 | 0,32 | 0,22 | 0,13 | 0,06 | 0,03 | |||||
| 8.65373 | 0.00 | 0,27 | 0,06 | −0,24 | −0,23 | 0,03 | 0,26 | 0,34 | 0,28 | 0,18 | 0.10 | 0,05 | 0,02 | ||||
| 9.0 | −0,09 | 0,25 | 0,14 | −0,18 | −0,27 | −0,06 | 0.20 | 0,33 | 0,31 | 0,21 | 0,12 | 0,06 | 0,03 | 0,01 | |||
| 10.0 | −0,25 | 0,04 | 0,25 | 0,06 | −0,22 | −0,23 | −0,01 | 0,22 | 0,32 | 0,29 | 0,21 | 0,12 | 0,06 | 0,03 | 0,01 | ||
| 12.0 | 0,05 | −0,22 | −0,08 | 0.20 | 0,18 | −0,07 | −0,24 | −0,17 | 0,05 | 0,23 | 0.30 | 0,27 | 0.20 | 0,12 | 0,07 | 0,03 | 0,01 |
Правило Карсона
Правило Карсона гласит , что почти вся (≈98 процентов ) мощность частотно-модулированного сигнала лежит в пределах полосы пропускания :
где , как определено выше, - пиковое отклонение мгновенной частоты от центральной несущей частоты , - индекс модуляции, который является отношением отклонения частоты к наивысшей частоте в модулирующем сигнале, а - наивысшая частота в модулирующем сигнале. Условием применения правила Карсона являются только синусоидальные сигналы. Для несинусоидальных сигналов:
где W — самая высокая частота в модулирующем сигнале, но несинусоидальном по своей природе, а D — коэффициент отклонения, который представляет собой отношение отклонения частоты к самой высокой частоте модулирующего несинусоидального сигнала.
Снижение шума
FM обеспечивает улучшенное отношение сигнал/шум (SNR), по сравнению, например, с AM . По сравнению с оптимальной схемой AM, FM обычно имеет худшее SNR ниже определенного уровня сигнала, называемого порогом шума, но выше более высокого уровня – полного улучшения или полного порога затухания – SNR намного улучшается по сравнению с AM. Улучшение зависит от уровня модуляции и отклонения. Для типичных каналов голосовой связи улучшения обычно составляют 5–15 дБ. FM-вещание с использованием более широкого отклонения может достичь еще больших улучшений. Дополнительные методы, такие как предварительное выделение более высоких звуковых частот с соответствующим устранением выделения в приемнике, обычно используются для улучшения общего SNR в схемах FM. Поскольку сигналы FM имеют постоянную амплитуду, приемники FM обычно имеют ограничители, которые удаляют шум AM, дополнительно улучшая SNR. [8] [9]
Выполнение
Модуляция
Сигналы FM могут генерироваться с использованием прямой или косвенной частотной модуляции:
- Прямая ЧМ-модуляция может быть достигнута путем прямой подачи сообщения на вход генератора, управляемого напряжением .
- Для косвенной модуляции FM сигнал сообщения интегрируется для генерации фазомодулированного сигнала . Это используется для модуляции кварцевого генератора , а результат передается через умножитель частоты для получения сигнала FM. При этой модуляции генерируется узкополосная FM, которая позже переходит в широкополосную FM, и поэтому модуляция известна как косвенная модуляция FM. [10]
Демодуляция

Существует множество схем детекторов FM. Распространенным методом восстановления информационного сигнала является дискриминатор Фостера-Сили или детектор отношения . Фазовая автоподстройка частоты может использоваться в качестве демодулятора FM. Детектор наклона демодулирует сигнал FM с помощью настроенной схемы, резонансная частота которой слегка смещена относительно несущей. По мере того, как частота повышается и понижается, настроенная схема обеспечивает изменяющуюся амплитуду отклика, преобразуя FM в AM. Приемники AM могут обнаруживать некоторые передачи FM таким образом, хотя это не обеспечивает эффективного средства обнаружения для вещания FM. В реализациях программно-определяемого радио демодуляция может выполняться с использованием преобразования Гильберта (реализованного в виде фильтра) для восстановления мгновенной фазы, а затем дифференцирования этой фазы (с использованием другого фильтра) для восстановления мгновенной частоты. В качестве альтернативы можно использовать сложный смеситель, за которым следует полосовой фильтр, для перевода сигнала в основную полосу частот, а затем действовать, как и прежде.
Приложения
эффект Доплера
Когда летучая мышь , использующая эхолокацию , приближается к цели, ее исходящие звуки возвращаются в виде эха, которое смещено вверх по частоте с помощью эффекта Доплера. У некоторых видов летучих мышей, которые производят эхолокационные сигналы с постоянной частотой (CF), летучие мыши компенсируют доплеровский сдвиг , понижая частоту своего сигнала по мере приближения к цели. Это сохраняет возвращающееся эхо в том же частотном диапазоне, что и обычный эхолокационный сигнал. Эта динамическая частотная модуляция называется компенсацией доплеровского сдвига (DSC) и была открыта Гансом Шницлером в 1968 году.
Накопитель на магнитной ленте
FM также используется на промежуточных частотах аналоговыми системами видеомагнитофонов (включая VHS ) для записи яркостных (черно-белых) частей видеосигнала. Обычно компонент цветности записывается как обычный сигнал AM, используя высокочастотный сигнал FM в качестве смещения . FM является единственным возможным методом записи яркостной («черно-белой») составляющей видео на магнитную ленту (и извлечения видео с нее) без искажений; видеосигналы имеют большой диапазон частотных компонентов — от нескольких герц до нескольких мегагерц , слишком широкий для работы с ними эквалайзеров из-за электронного шума ниже -60 дБ . FM также удерживает ленту на уровне насыщения, действуя как форма шумоподавления ; ограничитель может маскировать изменения в выходном сигнале воспроизведения, а эффект захвата FM удаляет пропечатку и опережающее эхо . Непрерывный пилот-тон, если его добавить к сигналу — как это было сделано в V2000 и многих форматах Hi-band — может держать под контролем механический джиттер и помогать в коррекции временной развертки .
Эти системы FM необычны тем, что у них отношение несущей к максимальной частоте модуляции меньше двух; сравните это с FM-аудиовещанием, где отношение составляет около 10 000. Рассмотрим, например, несущую 6 МГц, модулированную с частотой 3,5 МГц; по анализу Бесселя , первые боковые полосы находятся на 9,5 и 2,5 МГц, а вторые боковые полосы находятся на 13 МГц и -1 МГц. Результатом является боковая полоса с обращенной фазой на +1 МГц; при демодуляции это приводит к нежелательному выходу на 6 - 1 = 5 МГц. Система должна быть спроектирована таким образом, чтобы этот нежелательный выход был снижен до приемлемого уровня. [11]
Звук
FM также используется на аудиочастотах для синтеза звука. Эта техника, известная как синтез FM , была популяризирована ранними цифровыми синтезаторами и стала стандартной функцией в нескольких поколениях звуковых карт персональных компьютеров .
Радио

Эдвин Говард Армстронг (1890–1954) был американским инженером-электриком, который изобрел широкополосное частотное модуляционное (FM) радио. [12] Он запатентовал регенеративную схему в 1914 году, супергетеродинный приемник в 1918 году и суперрегенеративную схему в 1922 году. [13] Армстронг представил свою работу «Метод уменьшения помех в радиосигнализации с помощью системы частотной модуляции» (в которой впервые было описано FM-радио) перед Нью-Йоркским отделением Института радиоинженеров 6 ноября 1935 года. Работа была опубликована в 1936 году. [14]
Как следует из названия, широкополосная FM (WFM) требует более широкой полосы пропускания сигнала , чем амплитудная модуляция эквивалентным модулирующим сигналом; это также делает сигнал более устойчивым к шуму и помехам . Частотная модуляция также более устойчива к явлениям затухания амплитуды сигнала. В результате FM была выбрана в качестве стандарта модуляции для высокочастотной, высококачественной радиопередачи , отсюда и термин « FM-радио » (хотя в течение многих лет BBC называла его «VHF-радио», потому что коммерческое FM-вещание использует часть диапазона VHF — диапазон FM-вещания ). FM- приемники используют специальный детектор для FM-сигналов и демонстрируют явление, известное как эффект захвата , при котором тюнер «захватывает» более сильную из двух станций на той же частоте, отклоняя другую (сравните это с аналогичной ситуацией на AM-приемнике, где обе станции можно слышать одновременно). Дрейф частоты или отсутствие селективности могут привести к тому, что одна станция будет обойдена другой на соседнем канале . Дрейф частоты был проблемой в ранних (или недорогих) приемниках; недостаточная селективность может повлиять на любой тюнер.
Широкополосный FM-сигнал также может использоваться для передачи стереосигнала ; это делается с помощью мультиплексирования и демультиплексирования до и после процесса FM. Процесс модуляции и демодуляции FM идентичен в стерео- и монофонических процессах.
FM обычно используется на частотах радиосвязи VHF для высококачественной трансляции музыки и речи . В вещательных службах, где важна точность воспроизведения звука, обычно используется широкополосная FM. Аналоговый телевизионный звук также транслируется с использованием FM. Узкополосная FM используется для голосовой связи в коммерческих и любительских радиоустановках . В двусторонней радиосвязи узкополосная FM (NBFM) используется для экономии полосы пропускания для наземных мобильных, морских мобильных и других радиослужб.
Высокоэффективный усилитель коммутации радиочастот может использоваться для передачи сигналов FM (и других сигналов с постоянной амплитудой ). Для заданной силы сигнала (измеренной на антенне приемника) усилители коммутации потребляют меньше энергии батареи и обычно стоят меньше, чем линейный усилитель . Это дает FM еще одно преимущество перед другими методами модуляции, требующими линейных усилителей, такими как AM и QAM .
Имеются сведения, что 5 октября 1924 года профессор Михаил Андреевич Бонч-Бруевич во время научно-технической беседы в Нижегородской радиолаборатории доложил о своем новом методе телефонии, основанном на изменении периода колебаний. Демонстрация частотной модуляции проводилась на лабораторном макете. [15]
Технологии поддержки слуха
Частотно-модулированные системы являются широко распространенной и коммерчески доступной вспомогательной технологией , которая делает речь более понятной за счет улучшения соотношения сигнал/шум в ухе пользователя. Их также называют слуховыми тренажерами , термин, который относится к любой системе усиления звука, не классифицируемой как слуховой аппарат . Они усиливают уровни сигнала от источника на 15-20 децибел. [16] FM-системы используются людьми с нарушениями слуха, а также детьми, чей слух страдает от таких расстройств, как нарушение слуховой обработки или СДВГ . [17] Для людей с нейросенсорной потерей слуха FM-системы обеспечивают лучшее восприятие речи, чем слуховые аппараты. Их можно сочетать с заушными слуховыми аппаратами, чтобы пользователь мог менять настройки. [18] FM-системы более удобны и экономичны, чем альтернативы, такие как кохлеарные имплантаты , но многие пользователи используют FM-системы нечасто из-за их заметности и необходимости подзарядки. [19]
Смотрите также
- Амплитудная модуляция
- Радиолокатор с непрерывной частотной модуляцией
- Чириканье
- FM-вещание
- FM-стерео
- FM-UWB (FM и сверхширокополосный)
- История радио
- Модуляция , для списка других методов модуляции
- Фазовая модуляция
Ссылки
- ^ Джибилиско, Стэн (2002). Самостоятельно изучите электричество и электронику . McGraw-Hill Professional. стр. 477. ISBN 978-0-07-137730-0.
частотная манипуляция кодом Морзе, отправленная с использованием fsk.
- ^ Ратледж, Дэвид Б. (1999). Электроника радио. Cambridge University Press. стр. 310. ISBN 978-0-521-64645-1.
- ^ Б. Боашаш, редактор, Анализ и обработка частотно-временных сигналов – Полный справочник , Elsevier Science, Оксфорд, 2003; ISBN 0-08-044335-4
- ^ Фарук, Салех (2017). Радиочастотная модуляция стала проще (PDF) . Springer Cham. стр. 33–37. ISBN 978-3-319-41200-9.
- ^ ab TG Thomas, SC Sekhar Теория коммуникации , Tata-McGraw Hill 2005, ISBN 0-07-059091-5 стр. 136
- ^ Дер, Лоуренс. "Частотная модуляция (FM) Учебное пособие" (PDF) . Silicon Laboratories . S2CID 48672999. Архивировано из оригинала (PDF) 2014-10-21 . Получено 17 октября 2019 .
- ^ Лати, Б. П. (1968). Системы связи , стр. 214–17. Нью-Йорк: John Wiley and Sons, ISBN 0-471-51832-8 .
- ^ HP Westman, ред. (1970). Справочные данные для радиоинженеров (пятое изд.). Howard W. Sams & Co. стр. 21–11.
- ^ Алан Блум (2010). "Глава 8. Модуляция". В H. Ward Silver; Mark J. Wilson (ред.). Справочник ARRL по радиосвязи . Американская лига радиорелейной связи. стр. 8.7. ISBN 978-0-87259-146-2.
- ^ Хайкин, Саймон [редактор]. (2001). Системы связи , 4-е изд.
- ^ "FM-системы исключительной полосы пропускания" Proc. IEEE т. 112, № 9, стр. 1664, сентябрь 1965 г.
- ^ А. Майкл Нолл (2001). Принципы современных коммуникационных технологий . Artech House. стр. 104. ISBN 978-1580532846.
- ^ США 1342885
- ^ Армстронг, Э. Х. (май 1936 г.). «Метод уменьшения помех в радиосигнализации с помощью системы частотной модуляции». Труды IRE . 24 (5). IRE: 689–740. doi :10.1109/JRPROC.1936.227383. S2CID 43628076.
- ^ Ф. Лбов. Новая система радиофона «Радиолюбитель». – 1924. – № 6. – С. 86.
- ^ ASHA Ad Hoc Committee on FM Systems (2002) [Оригинал, март 1994 г.]. Руководство по установке и мониторингу FM-систем (технический отчет) (пересмотренное издание). Американская ассоциация речи, языка и слуха . doi :10.1044/policy.GL2002-00010.
- ^ Schafer, Erin C.; Bryant, Danielle; Sanders, Katie; Baldus, Nicole; Algier, Katherine; Lewis, Audrey; Traber, Jordan; Layden, Paige; Amin, Aneeqa (1 июня 2014 г.). «Подгонка и проверка частотной модуляции у детей с нормальным слухом». Журнал Американской академии аудиологии . 25 (6): 529–540. doi :10.3766/jaaa.25.6.3. ISSN 1050-0545. PMID 25313543. Хост EBSCO 107832936 – через EBSCOhost .
- ^ Льюис, М. Саманта; Крэндалл, Карл С.; Валенте, Майкл; Энриетто Хорн, Джейн (2004). «Восприятие речи в шуме: направленные микрофоны против систем частотной модуляции (FM)». Журнал Американской академии аудиологии . 15 (6): 426–439. doi : 10.3766/jaaa.15.6.4 . PMID 15341224.
- ^ Макардл, Рэйчел; Абрамс, Харви Б.; Хнат Чисхолм, Тереза (2005). «Когда слуховые аппараты выходят из строя: история успеха FM». Журнал Американской академии аудиологии . 16 (10): 809–821. doi :10.3766/jaaa.16.10.5. Хост EBSCO 106441304 – через EBSCOhost .
Дальнейшее чтение
- Карлсон, А. Брюс (2001). Системы связи . Наука/Инженерия/Математика (4-е изд.). McGraw-Hill. ISBN 978-0-07-011127-1.
- Фрост, Гэри Л. (2010). Раннее FM-радио: инкрементальные технологии в Америке двадцатого века . Балтимор, Мэриленд: Johns Hopkins University Press. ISBN 978-0-8018-9440-4.
- Сеймур, Кен (2005) [1996]. «Частотная модуляция». Справочник по электронике (2-е изд.). CRC Press. С. 1188–1200. ISBN 0-8493-8345-5.
Внешние ссылки
- Онлайн-интерактивная демонстрация аналоговой модуляции с использованием Python на платформе Google Colab, автор C Foh.



![{\displaystyle {\begin{align}y(t)&=A_{c}\cos \left(2\pi \int _{0}^{t}f(\tau )d\tau \right)\\&=A_{c}\cos \left(2\pi \int _{0}^{t}\left[f_{c}+f_{\Delta }x_{m}(\tau )\right]d\tau \right)\\&=A_{c}\cos \left(2\pi f_{c}t+2\pi f_{\Delta }\int _{0}^{t}x_{m}(\tau )d\tau \right)\\\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a85546c0eab3462755f52bf3808a8b9f5083b38)





![{\displaystyle {\begin{align}y(t)&=A_{c}\cos \left(2\pi \left[f_{c}+f_{\Delta }x_{m}(t)\right]t\right)\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e21e0bf408a5afae4268fde1d3ec3d0ca150c3)

























