Разрыв потока жидкости

Разрыв нити жидкости — это процесс, при котором одна масса жидкости распадается на несколько меньших масс жидкости. Процесс характеризуется удлинением массы жидкости, образуя тонкие нитевидные области между более крупными узелками жидкости. Нитевидные области продолжают истончаться, пока не разорвутся, образуя отдельные капли жидкости.

Разрыв нити происходит, когда две жидкости или жидкость в вакууме образуют свободную поверхность с поверхностной энергией . Если площадь поверхности больше минимально необходимой для содержания объема жидкости, система имеет избыток поверхностной энергии . Система, не находящаяся в состоянии минимальной энергии, попытается перестроиться так, чтобы перейти в состояние с более низкой энергией, что приведет к разрыву жидкости на меньшие массы, чтобы минимизировать поверхностную энергию системы за счет уменьшения площади поверхности. Точный результат процесса разрыва нити зависит от поверхностного натяжения , вязкости , плотности и диаметра разрывающейся нити.

Изучение образования капель имеет долгую историю, впервые прослеживаемую еще со времен Леонардо да Винчи, который писал: ^[1]

«Как вода обладает цепкостью в себе и сцеплением между своими частицами. […] Это видно в процессе отделения капли от остатка, причем этот остаток растягивается настолько, насколько это возможно, под действием веса капли, которая его удлиняет; и после того, как капля отделяется от этой массы, масса возвращается вверх движением, противоположным природе тяжелых вещей».

Таким образом, он правильно объяснил падение капель гравитацией, а механизм, приводящий к разрыву нитей, — сцеплением молекул воды.

Первый правильный анализ разрыва нити жидкости был качественно определен Томасом Юнгом и математически Пьером-Симоном Лапласом между 1804 и 1805 годами. ^{[2] [3]} Они правильно приписали движущую силу разрыва нити свойствам поверхностного натяжения . Более того, они также вывели важность средней кривизны в создании избыточного давления в нити жидкости. С помощью своего анализа они показали, что поверхностное натяжение может вести себя двумя способами: упругий механизм, который может поддерживать висящую каплю, и механизм давления из-за капиллярного давления , который способствует разрыву нити.

В 1820-х годах итальянский физик и инженер-гидравлик Джорджио Бидоне изучал деформацию струй воды, вытекающих из отверстий различной формы. ^{[4] В 1833 году} Феликс Савар продолжил экспериментальную работу, используя стробоскопическую технику для количественного измерения разрыва нити. ^[5] Он отметил, что разрыв — это спонтанный процесс, происходящий без внешнего воздействия. Эта работа позволила ему определить, что капли образуются из струи, вытекающей из бака, с определенной скоростью, обратно пропорциональной радиусу сопла и пропорциональной давлению в баке. Эти наблюдения способствовали работе Жозефа Плато , который установил связь между разрывом струи и поверхностной энергией . ^[6] Плато смог определить самую нестабильную длину волны возмущения на жидкой нити, которая позже была пересмотрена лордом Рэлеем для учета динамики струи.

По мере того, как возмущение поверхности становится большим, необходимо применять нелинейную теорию. Поведение струй с большими возмущениями было экспериментально исследовано Магнусом и Ленардом . ^{[7] [8]} Их эксперименты помогли охарактеризовать капли-спутники, капли, которые производятся в дополнение к большой основной капле, посредством введения высокоскоростной фотографии. Высокоскоростная фотография в настоящее время является стандартным методом экспериментального анализа разрыва нити.

С появлением большей вычислительной мощности численное моделирование начало заменять экспериментальные усилия в качестве главного средства понимания распада жидкости. Однако по-прежнему сохраняется трудность в точном отслеживании свободной поверхности многих жидкостей из-за ее сложного поведения. Наибольший успех был достигнут с жидкостями с низкой и высокой вязкостью, где можно использовать метод граничного интеграла, поскольку известна функция Грина для обоих случаев. Доммермут и Юэ охарактеризовали безвихревой, невязкий поток этим методом, как и Шулькес. ^{[9] [10]} Янгрен и Акривос рассмотрели поведение пузырька в жидкости с высокой вязкостью. ^[11] Стоун и Лил расширили эту первоначальную работу, чтобы рассмотреть динамику отдельных капель. ^[12] Для жидкостей средней вязкости требуются полные моделирования с использованием уравнений Навье-Стокса с методами определения свободной поверхности, такими как установленный уровень и объем жидкости. Самая ранняя работа с полным моделированием Навье-Стокса была выполнена Фроммом, который сосредоточился на технологии струйной печати . ^​​[13] Такое моделирование остается активной областью исследований.

Процесс распада в жидкой нити или струе начинается с развития малых возмущений на свободной поверхности жидкости. Это известно как линейная теория распада жидкой нити. Эти возмущения всегда присутствуют и могут быть вызваны многочисленными источниками, включая вибрации контейнера с жидкостью или неравномерность касательного напряжения на свободной поверхности. В общем, эти возмущения принимают произвольную форму и поэтому их трудно рассматривать строго. Поэтому полезно выполнить преобразование Фурье возмущений, чтобы разложить произвольные возмущения на возмущения различных отдельных длин волн на поверхности нити. При этом это позволяет определить, какие длины волн возмущения будут расти, а какие будут затухать со временем. ^[14]

Рост и затухание длин волн можно определить, исследуя изменение давления, которое длина волны возмущения оказывает на внутреннюю часть нити жидкости. Изменения внутреннего давления нити вызываются капиллярным давлением , поскольку свободная поверхность нити деформируется. Капиллярное давление является функцией средней кривизны интерфейса в заданном месте на поверхности, то есть давление зависит от двух радиусов кривизны, которые задают форму поверхности. В пределах утонченной области нити жидкости, подвергающейся разрыву, первый радиус кривизны меньше радиуса кривизны в утолщенной области, что приводит к градиенту давления, который будет стремиться вытеснять жидкость из утонченных областей в утолщенные. Однако второй радиус кривизны остается важным для процесса разрыва. Для некоторых длин волн возмущения эффект второго радиуса кривизны может преодолеть эффект давления первого радиуса кривизны, вызывая большее давление в утолщенных областях, чем в утонченных областях. Это будет толкать жидкость обратно к истонченным областям и стремиться вернуть нить к ее первоначальной, ненарушенной форме. Однако для других длин волн возмущения капиллярное давление, вызванное вторым радиусом кривизны, усилит давление первого радиуса кривизны. Это будет перемещать жидкость из истонченных в утолщенные области и еще больше способствовать разрыву нити.

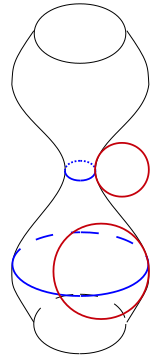
Длина волны возмущения, таким образом, является критическим параметром при определении того, распадется ли данная нить жидкости на более мелкие массы жидкости. Строгое математическое исследование длин волн возмущения может привести к соотношению, показывающему, какие длины волн являются стабильными для данной нити, а также какие длины волн возмущения будут расти наиболее быстро. Размер масс жидкости, образующихся в результате распада нити жидкости, может быть аппроксимирован длинами волн возмущения, которые растут наиболее быстро.

Хотя линейная теория полезна при рассмотрении роста малых возмущений на свободной поверхности, когда возмущения вырастают до значительной амплитуды, нелинейные эффекты начинают доминировать в поведении разрыва. Нелинейное поведение нити управляет ее окончательным разрывом и в конечном итоге определяет окончательную форму и количество полученных масс жидкости.

Нелинейность улавливается с помощью самоподобия . Самоподобие предполагает, что поведение нити жидкости, когда радиус приближается к нулю, такое же, как поведение нити жидкости, когда она имеет некоторый конечный радиус. Детальное понимание поведения нелинейной нити требует использования асимптотических разложений для генерации соответствующего поведения масштабирования. Было найдено множество решений для нелинейного поведения нитей жидкости на основе сил, которые имеют значение в конкретных обстоятельствах. ^{[15] [16] [17]}

То, как струя или поток жидкости претерпевает разрыв, регулируется несколькими параметрами, среди которых число Рейнольдса , число Вебера , число Онезорге и длина волны возмущения . Хотя эти числа являются обычными в механике жидкости, параметры, выбранные в качестве масштабов, должны соответствовать разрыву потока. Чаще всего в качестве масштаба длины выбирается радиус потока жидкости, в то время как скорость чаще всего принимается за скорость движения объемной жидкости. Однако эти масштабы могут меняться в зависимости от характеристик рассматриваемой задачи.

Число Рейнольдса — это соотношение между инерцией и вязкими эффектами внутри нити. При больших числах Рейнольдса эффекты движения нити намного больше, чем вязкая диссипация. Вязкость оказывает лишь минимальное демпфирующее воздействие на нить. При малых числах Рейнольдса вязкая диссипация велика, и любые возмущения быстро затухают от нити.

Число Вебера — это соотношение между эффектами инерции и поверхностного натяжения внутри нити. Когда число Вебера велико, инерция нити велика, что препятствует тенденции поверхностного натяжения сглаживать изогнутые поверхности. При малых числах Вебера изменения капиллярного давления из-за поверхностных возмущений велики, и поверхностное натяжение доминирует над поведением нити.

Число Онезорге — это соотношение между эффектами вязкости и поверхностного натяжения внутри нити. Поскольку оно устраняет эффекты инерции и необходимость в шкале скорости, часто бывает удобнее выражать масштабные соотношения в терминах числа Онезорге, а не чисел Рейнольдса и Вебера по отдельности.

Длина волны возмущения — это характерная длина возмущения на поверхности струи, предполагающая, что любое произвольное возмущение может быть разложено с помощью преобразования Фурье на его составляющие компоненты. Длина волны возмущения имеет решающее значение для определения того, будет ли конкретное возмущение расти или затухать со временем.

Линейная устойчивость жидкостей с низкой вязкостью была впервые получена Плато в 1873 году. ^[14] Однако его решение стало известно как неустойчивость Рэлея-Плато из-за расширения теории лордом Рэлеем для включения жидкостей с вязкостью. Неустойчивость Рэлея-Плато часто используется как вводный случай для гидродинамической устойчивости, а также для анализа возмущений.

Плато рассмотрел устойчивость потока жидкости, когда присутствовали только инерционные и поверхностные эффекты натяжения. Разложив произвольное возмущение на свободной поверхности на его конститутивные гармоники/длины волн, он смог вывести условие устойчивости струи в терминах возмущения:

${\displaystyle \omega ^{2}={\frac {\sigma k}{\rho a^{2}}}{\frac {I_{1}(ka)}{I_{0}(ka)}}\left(1-k^{2}a^{2}\right),}$

где ω — скорость роста возмущения, σ — поверхностное натяжение жидкостей, k — волновое число возмущения, ρ — плотность жидкости, a — начальный радиус невозмущенной жидкости, а I — модифицированная функция Бесселя первого рода. Вычисляя скорость роста как функцию волнового числа, можно определить, что самая быстрорастущая длина волны возмущения происходит при:

${\displaystyle \lambda _{\text{макс}}\приблизительно 9,02а.}$

Длина волны максимальной неустойчивости увеличивается с увеличением радиуса нити жидкости. Важно, что неустойчивые моды возможны только при:

${\displaystyle ка<1.}$

Рейнольдс и позже Томотика расширили работу Плато, чтобы рассмотреть линейную устойчивость вязких нитей. Рэлей нашел решение для устойчивости вязкой нити вязкости без присутствия внешней жидкости. ^[18] Томокита нашел решение для устойчивости жидкой нити в присутствии внешней жидкости с ее собственной вязкостью . ^[19] Он рассмотрел три случая, когда вязкость жидкой нити была намного больше, чем вязкость внешней среды, вязкость внешней среды была намного больше, чем вязкость жидкой нити, и общий случай, когда жидкости имеют произвольную вязкость.${\displaystyle \mu _{A}}$${\displaystyle \mu _{B}}$

Для предельного случая, когда жидкая нить намного более вязкая, чем внешняя среда, вязкость внешней среды полностью выпадает из скорости роста. Таким образом, скорость роста становится функцией только начального радиуса нити, длины волны возмущения, поверхностного натяжения нити и вязкости нити.

${\displaystyle \omega ={\frac {\sigma \left(k^{2}a^{2}-1\right)}{2a\mu _{A}}}{\frac {1}{k^{2}a^{2}+1-k^{2}a^{2}I_{0}^{2}(кa)/I_{1}^{2}(кa)}}}$

Построив график, можно обнаружить, что самые длинные длины волн являются самыми нестабильными. Что важно, можно отметить, что вязкость жидкой нити не влияет на то, какие длины волн будут стабильными. Вязкость действует только на уменьшение того, насколько быстро данное возмущение будет расти или затухать со временем.

Примерами того, когда применим этот случай, являются случаи, когда практически любая жидкость подвергается разрыву нитей/струй в воздушной среде.

Для предельного случая, когда внешняя среда жидкой нити намного более вязкая, чем сама нить, вязкость жидкой нити полностью падает от скорости роста возмущения. Скорость роста, таким образом, становится функцией только начального радиуса нити, длины волны возмущения, поверхностного натяжения нити, вязкости внешней среды и функций Бесселя второго порядка второго рода.

${\displaystyle \omega ={\frac {\sigma \left(1-k^{2}a^{2}\right)}{2a\mu _{B}}}{\frac {1}{k^{2}a^{2}+1-k^{2}a^{2}K_{0}^{2}(к)/K_{1}^{2}(к)}}}$

Если бы кто-то построил график скорости роста как функции длины волны возмущения, то он обнаружил бы, что самые нестабильные длины волн снова возникают при самых длинных волнах, а вязкость внешней среды будет только уменьшать скорость роста или затухания возмущения со временем.

Примерами случаев, когда этот случай применим, являются случаи, когда пузырьки газа попадают в жидкость или когда вода попадает в мед.

Общий случай для двух вязких жидкостей гораздо сложнее решить напрямую. Томотика выразил свое решение как:

${\displaystyle \omega ={\frac {\sigma \left(1-k^{2}a^{2}\right)}{2a\mu _{B}}}\Phi (ka)}$

где было определено как:${\displaystyle \Фи}$

${\displaystyle {\begin{aligned}\Phi (ka)={}&{\frac {N(ka)}{D(ka)}}\\N(ka)={}&I_{1}(ka)\Delta _{1}-\{kaI_{0}(ka)-I_{1}(ka)\}\Delta _{2}\\D(ka)={} & {\frac {\mu _{A}}{\mu _{B}}}\{kaI_{0}(ka)-I_{1}(ka)\}\Delta _{1}-{\frac {\mu _{A}}{\mu _{B}}}\left\{\left(k^{2}a^{2}+1\right)I_{1}(ka)-kaI_{0}(ka)\right\}\Delta _{2}\\&-\{kaK_{0}(ka)+K_{1}(ka)\}\Delta _{3}-\left\{\left(k^{2}a^{2}+1\right)K_{1}(ka)+kaK_{0}(ka)\right\}\Delta _{4}\end{aligned}}}$

Коэффициенты проще всего выразить как определители следующих матриц:${\displaystyle \Дельта}$

${\displaystyle {\begin{aligned}\Delta _{1}&={\begin{vmatrix}kaI_{0}(ka)-I_{1}(ka)&K_{1}(ka)&-kaK_{0}(ka)-K_{ 1}(ka)\\I_{0}(ka)+kaI_{1}(ka)&-K_{0}(ka)&-K_{0}(ka)+kaK_{1}(ka)\\{\frac {\mu _{A}}{\mu _{B}}}kaI_{0}(ka)&K_{1}(ka)&-kaK_{0}(ka)\end{vmatrix}}\\[3pt]\Delta _{2}&={\begin{vmatrix}I_{1}(ka)&K_{1}(ka)&-kaK_{0}(ka)-K_{1}(ka)\\I_{0}(ka)&-K_{0}(ka)&-K_{0}(ka)+kaK_{1}(ka)\\{\frac {\mu _{A}}{\mu _{B}}}I_{1}(ka)&K_{1}(ka)&-kaK_{0}(ka)\end{vmatrix}}\\[3pt]\Delta _{3}&={\begin{vmatrix}I_{1}(ka)&kaI_{0}(ka)-I_{1}(ka)&-kaK_{0}(ka)-K_{ 1}(ka)\\I_{0}(ka)&I_{0}(ka)+kaI_{1}(ka)&-K_{0}(ka)+kaK_{1}(ka)\\{\frac {\mu _{A}}{\mu _{B}}}I_{1}(ka)&{\frac {\mu _{A}}{\mu _{B}}}kaI_{0}(ka)&-kaK_{0}(ka)\end{vmatrix}}\\[3pt]\Delta _{4}&={\begin{vmatrix}I_{1}(ka)&kaI_{0}(ka)-I_{1}(ka)&K_{1}(ka)\\I_{0}(ka)&I_{0}(ka)+kaI_{1}(ka)&-K_{0}(ka)\\{\frac {\mu _{A}}{\mu _{B}}}I_{1}(ka)&{\frac {\mu _{a}}{\mu _{B}}}kaI_{0}(ka)&K_{1}(ka)\end{vmatrix}}\end{aligned}}}$

Полученное решение остается функцией как вязкости нити и внешней среды, так и длины волны возмущения. Наиболее нестабильная комбинация вязкостей и возмущения возникает при .${\displaystyle \mu _{A}/\mu _{B}\приблизительно 0,28}$${\displaystyle \лямбда \приблизительно 10,66a}$

Для большинства приложений использование общего случая не является необходимым, поскольку две рассматриваемые жидкости имеют существенно разные вязкости, что позволяет использовать один из предельных случаев. Однако некоторые случаи, такие как смешивание масел или масел и воды, могут потребовать использования общего случая.

Капли-сателлиты, также известные как вторичные капли, — это капли, образующиеся в процессе разрыва нити в дополнение к большой основной капле. Капли возникают, когда нить, с помощью которой основная капля подвешена к большей массе жидкости, сама отрывается от массы жидкости. Жидкость, содержащаяся в нити, может оставаться как единая масса или распадаться из-за возмущений отдачи, налагаемых на нее разделением основной капли. В то время как образование капель-сателлитов можно предсказать на основе свойств жидкости, их точное местоположение и объем предсказать невозможно. ^{[20] [21]}

В целом, вторичные капли являются нежелательным явлением, особенно в приложениях, где важна точность осаждения капель. Производство спутниковых капель регулируется нелинейной динамикой проблемы вблизи конечных стадий разрыва нити.

Многочисленные примеры разрыва потоков жидкости существуют в повседневной жизни. Это одно из наиболее распространенных явлений механики жидкости, с которым мы сталкиваемся, и поэтому большинство уделяет этому процессу мало внимания.

Капающая вода — это обычное явление. Когда вода вытекает из крана, нить, прикрепленная к крану, начинает сужаться, в конечном итоге до такой степени, что основная капля отрывается от поверхности. ^[22] Нить не может достаточно быстро втянуться в кран, чтобы предотвратить разрыв, и поэтому распадается на несколько маленьких капель-спутников. ^[22]

Воздушные пузырьки — еще одно распространенное явление распада. Когда воздух попадает в емкость с жидкостью, например, в аквариум, нить снова сужается у основания, образуя пузырь. Выдувание пузырей из соломинки в стакан происходит примерно таким же образом.

Эксперимент с каплей смолы — это известный эксперимент по разделению жидкости с использованием высоковязкого смоляного пека. Скорость разделения замедлена до такой степени, что с 1927 года упало всего 11 капель.

Мед достаточно вязкий, поэтому поверхностные возмущения, которые приводят к разрыву, почти полностью гасятся медовыми нитями. Это приводит к образованию длинных нитей меда, а не отдельных капель.