Ферримагнетизм
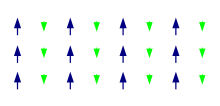

Ферримагнитный материал — это материал, в котором популяции атомов имеют противоположные магнитные моменты , как в антиферромагнетизме , но эти моменты не равны по величине, поэтому сохраняется спонтанная намагниченность . [1] Это может происходить, например, когда популяции состоят из разных атомов или ионов (например, Fe2 + и Fe3 + ).
Подобно ферромагнитным веществам, ферримагнитные вещества притягиваются магнитами и могут быть намагничены для создания постоянных магнитов . Старейшее известное магнитное вещество, магнетит (Fe 3 O 4 ), является ферримагнетиком, но классифицировалось как ферромагнетик до того, как Луи Неель открыл ферримагнетизм в 1948 году. [2] После открытия были найдены многочисленные применения ферримагнитных материалов, такие как пластины жестких дисков и биомедицинские приложения.
История
До двадцатого века все встречающиеся в природе магнитные вещества назывались ферромагнетиками. В 1936 году Луи Неель опубликовал статью, в которой предположил существование новой формы кооперативного магнетизма, названной им антиферромагнетизмом. [3] Работая с Mn2Sb , французский физик Шарль Гийо обнаружил, что современные теории магнетизма недостаточны для объяснения поведения материала, и создал модель для объяснения этого поведения. [4] В 1948 году Неель опубликовал статью о третьем типе кооперативного магнетизма, основанном на предположениях модели Гийо. Он назвал его ферримагнетизмом. В 1970 году Неель был награжден за свою работу в области магнетизма Нобелевской премией по физике . [5]
Физическое происхождение

Ферримагнетизм имеет то же физическое происхождение, что и ферромагнетизм и антиферромагнетизм . В ферримагнитных материалах намагниченность также вызвана комбинацией диполь-дипольных взаимодействий и обменных взаимодействий, возникающих в результате принципа исключения Паули . Главное отличие состоит в том, что в ферримагнитных материалах в элементарной ячейке материала находятся разные типы атомов . Пример этого можно увидеть на рисунке выше. Здесь атомы с меньшим магнитным моментом указывают в противоположном направлении от атомов с большими моментами. Такое расположение похоже на то, что присутствует в антиферромагнитных материалах, но в ферримагнитных материалах суммарный момент не равен нулю, поскольку противоположные моменты различаются по величине.
Ферримагнетики имеют критическую температуру, выше которой они становятся парамагнитными , как и ферромагнетики. [6] При этой температуре (называемой температурой Кюри ) происходит фазовый переход второго рода , [7] и система больше не может поддерживать спонтанную намагниченность. Это происходит потому, что при более высоких температурах тепловое движение достаточно сильное, чтобы превышать тенденцию диполей к выравниванию.
Вывод
Существуют различные способы описания ферримагнетиков, простейший из которых — теория среднего поля . В теории среднего поля поле, действующее на атомы, можно записать как
где - приложенное магнитное поле , а - поле, вызванное взаимодействием между атомами. Следующее предположение тогда
Здесь - средняя намагниченность решетки, а - коэффициент молекулярного поля. Когда мы допускаем , что и зависят от положения и ориентации, мы можем записать это в виде
где - поле, действующее на i -ю подструктуру, и - коэффициент молекулярного поля между i -ю и k -ю подструктурами. Для двухатомной решетки мы можем обозначить два типа узлов, a и b . Мы можем обозначить число магнитных ионов в единице объема, долю магнитных ионов на узлах a и долю на узлах b . Это тогда дает
Можно показать, что и что если структуры не идентичны, то благоприятствует параллельному выравниванию и , тогда как благоприятствует антипараллельному выравниванию. Для ферримагнетиков , поэтому будет удобно взять как положительную величину и явно написать знак минус перед ней. Для полных полей на a и b это тогда дает
Далее, мы введем параметры и которые дают соотношение между силами взаимодействий. Наконец, мы введем приведенные намагниченности
со спином i -го элемента. Это дает для полей:
Решения этих уравнений (здесь опущены) затем даются как
где — функция Бриллюэна . Простейший случай для решения — . Поскольку , то это дает следующую пару уравнений:
с и . Эти уравнения не имеют известного аналитического решения, поэтому их необходимо решить численно, чтобы найти температурную зависимость .
Влияние температуры
В отличие от ферромагнетизма, кривые намагничивания ферримагнетизма могут принимать множество различных форм в зависимости от силы взаимодействий и относительного содержания атомов. Наиболее примечательными примерами этого свойства являются то, что направление намагничивания может меняться при нагревании ферримагнитного материала от абсолютного нуля до его критической температуры, и что сила намагничивания может увеличиваться при нагревании ферримагнитного материала до критической температуры, оба из которых не могут происходить для ферромагнитных материалов. Эти температурные зависимости также экспериментально наблюдались в NiFe 2/5 Cr 8/5 O 4 [8] и Li 1/2 Fe 5/4 Ce 5/4 O 4 . [9]
Температура ниже температуры Кюри , но при которой противоположные магнитные моменты равны (что приводит к нулевому суммарному магнитному моменту), называется точкой компенсации намагничивания. Эта точка компенсации легко наблюдается в гранатах и сплавах редкоземельных металлов с переходными металлами (RE-TM). Кроме того, ферримагнетики также могут иметь точку компенсации углового момента , в которой суммарный угловой момент обращается в нуль. Эта точка компенсации имеет решающее значение для достижения быстрого перемагничивания в устройствах магнитной памяти.
Влияние внешних полей

Когда ферримагнетики подвергаются воздействию внешнего магнитного поля, они демонстрируют то, что называется магнитным гистерезисом , когда магнитное поведение зависит от истории магнита. Они также демонстрируют насыщенную намагниченность ; эта намагниченность достигается, когда внешнее поле достаточно сильное, чтобы заставить все моменты выровняться в одном направлении. Когда эта точка достигнута, намагниченность не может увеличиться, так как больше нет моментов для выравнивания. Когда внешнее поле снимается, намагниченность ферримагнетика не исчезает, но остается ненулевая намагниченность. Этот эффект часто используется в приложениях магнитов. Если впоследствии приложить внешнее поле в противоположном направлении, магнит будет размагничиваться дальше, пока в конечном итоге не достигнет намагниченности . Такое поведение приводит к тому, что называется петлей гистерезиса . [10]
Свойства и применение
Ферримагнитные материалы обладают высоким удельным сопротивлением и анизотропными свойствами. Анизотропия фактически индуцируется внешним приложенным полем. Когда это приложенное поле выравнивается с магнитными диполями, оно вызывает чистый магнитный дипольный момент и заставляет магнитные диполи прецессировать с частотой, контролируемой приложенным полем, называемой Ларморовой или частотой прецессии . В качестве конкретного примера, микроволновый сигнал, циркулярно поляризованный в том же направлении, что и эта прецессия, сильно взаимодействует с магнитными дипольными моментами ; когда он поляризован в противоположном направлении, взаимодействие очень слабое. Когда взаимодействие сильное, микроволновый сигнал может проходить через материал. Это направленное свойство используется при создании микроволновых устройств, таких как изоляторы , циркуляторы и гираторы . Ферримагнитные материалы также используются для производства оптических изоляторов и циркуляторов . Ферримагнитные минералы в различных типах горных пород используются для изучения древних геомагнитных свойств Земли и других планет. Эта область исследований известна как палеомагнетизм . Кроме того, было показано, что ферримагнетики, такие как магнетит, могут использоваться для хранения тепловой энергии . [11]
Примеры
Самый старый известный магнитный материал, магнетит , является ферримагнитным веществом. Тетраэдрические и октаэдрические узлы его кристаллической структуры демонстрируют противоположный спин. Другие известные ферримагнитные материалы включают иттриевый железный гранат (YIG); кубические ферриты, состоящие из оксидов железа с другими элементами , такими как алюминий , кобальт , никель , марганец и цинк ; и гексагональные или шпинельные ферриты, включая феррит рения, ReFe2O4 , PbFe12O19 и BaFe12O19 и пирротин , Fe1 − xS . [ 12 ]
Ферримагнетизм может также иметь место в одиночных молекулярных магнитах . Классическим примером является двенадцатиядерная молекула марганца с эффективным спином S = 10, полученная из антиферромагнитного взаимодействия на металлических центрах Mn(IV) с металлическими центрами Mn(III) и Mn(II). [13]
Смотрите также
- Энергия анизотропии – энергия в определенном направленииPages displaying wikidata descriptions as a fallback
- Орбитальное намагничивание
Ссылки
- ^ Спалдин, Никола А. (2011). Магнитные материалы: основы и применение (2-е изд.). Кембридж: Cambridge University Press. ISBN 978-0-521-88669-7. OCLC 607986416.
- ^ Неель, М. Луи (1948). «Магнитные свойства ферритов; ферримагнетизм и антиферромагнетизм» (PDF) . Анналы тела . 12 (3): 137–198. Бибкод : 1948АнФ...12..137Н. дои : 10.1051/anphys/194812030137. ISSN 0003-4169. S2CID 126111103.
- ^ Неель, Луи (1936). «Магнитные свойства металла и энергия взаимодействия между магнитными атомами». Анналы тела . 11 (5): 232–279. Бибкод : 1936АнФ...11..232Н. дои : 10.1051/anphys/193611050232. ISSN 0003-4169.
- ^ Смарт, Дж. Сэмюэл (сентябрь 1955 г.). «Теория ферримагнетизма Нееля». American Journal of Physics . 23 (6): 356–370. Bibcode : 1955AmJPh..23..356S. doi : 10.1119/1.1934006. ISSN 0002-9505.
- ^ "Нобелевская премия по физике 1970 года". NobelPrize.org . Получено 2021-01-26 .
- ^ Саймон, Стивен Х. (21 июня 2013 г.). Основы твердого тела в Оксфорде (1-е изд.). Оксфорд. ISBN 978-0-19-150210-1. OCLC 851099021.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Бланделл, Стивен; Бланделл, Кэтрин М. (2010). Концепции в тепловой физике (2-е изд.). Оксфорд: Oxford University Press. ISBN 978-0-19-956209-1. OCLC 607907330.
- ^ Цусима, Тачиро (август 1963 г.). «Магнитные свойства феррит-хромитовых серий никеля и кобальта». Журнал Физического общества Японии . 18 (8): 1162–1166. Bibcode : 1963JPSJ...18.1162T. doi : 10.1143/jpsj.18.1162. ISSN 0031-9015.
- ^ Гортер, Э. В.; Шулькес, Дж. А. (1953-05-01). «Обращение спонтанной намагниченности как функция температуры в шпинелях LiFeCr». Physical Review . 90 (3): 487–488. Bibcode : 1953PhRv...90..487G. doi : 10.1103/physrev.90.487.2. ISSN 0031-899X.
- ^ Солер, Маг; Патерно, Л.Г. (01.01.2017), Да Роз, Алессандра Л.; Феррейра, Маристела; де Лима Лейте, Фабио; Оливейра, Освальдо Н. (ред.), «Глава 6. Магнитные наноматериалы», «Наноструктуры » , William Andrew Publishing, стр. 147–186, doi : 10.1016/b978-0-323-49782-4.00006-1, ISBN 978-0-323-49782-4, получено 2021-01-25.
- ^ Гросу, Ярослав; Фаик, Абдессамад; Ортега-Фернандес, Иньиго; Д'Агуанно, Бруно (март 2017 г.). «Природный магнетит для хранения тепловой энергии: превосходные термофизические свойства, обратимый переход скрытого тепла и контролируемая теплопроводность». Материалы и солнечные элементы для солнечной энергетики . 161 : 170–176. doi : 10.1016/j.solmat.2016.12.006 .
- ^ Кляйн, К. и Датроу, Б., Минералогия, 23-е изд., Wiley, стр. 243.
- ^ Sessoli, Roberta; Tsai, Hui Lien; Schake, Ann R.; Wang, Sheyi; Vincent, John B.; Folting, Kirsten; Gatteschi, Dante; Christou, George; Hendrickson, David N. (1993). "Высокоспиновые молекулы: [Mn 12 O 12 (O 2 CR) 16 (H 2 O) 4 ]". J. Am. Chem. Soc . 115 (5): 1804–1816. doi :10.1021/ja00058a027.









































