Теория короля драконов
Событие, которое одновременно является чрезвычайно масштабным по своему эффекту и уникальным по своему происхождению
Обложка сборника статей о королях драконов [1]

Король драконов — это двойная метафора для события, которое одновременно является чрезвычайно большим по размеру или эффекту («король») и рождено уникальным происхождением («дракон») относительно своих сверстников (других событий из той же системы). События DK генерируются или соответствуют таким механизмам, как положительная обратная связь , переломные моменты , бифуркации и фазовые переходы , которые имеют тенденцию происходить в нелинейных и сложных системах и служат для усиления событий короля драконов до экстремальных уровней. Понимая и отслеживая эту динамику, можно получить некоторую предсказуемость таких событий. [1] [2] [3]

Теория короля драконов была разработана Дидье Сорнеттом , который выдвигает гипотезу, что многие кризисы на самом деле являются DK, а не черными лебедями , то есть они могут быть в некоторой степени предсказуемы. Учитывая важность кризисов для долгосрочной организации различных систем, теория DK призывает уделять особое внимание изучению и мониторингу экстремальных ситуаций и принимать динамический подход. С научной точки зрения такие экстремальные ситуации интересны, поскольку они могут раскрывать основные, часто скрытые, организующие принципы. С практической точки зрения, следует изучать экстремальные риски, но не забывать, что значительная неопределенность будет присутствовать почти всегда и должна быть тщательно учтена при принятии решений относительно управления рисками и проектирования.

Теория короля драконов связана с такими концепциями, как теория черного лебедя, выбросы , сложные системы , нелинейная динамика , степенные законы , теория экстремальных значений , прогнозирование , экстремальные риски и управление рисками .

Черные лебеди и короли-драконы

Черный лебедь может считаться метафорой события, которое является неожиданным (для наблюдателя), имеет большой эффект и, после наблюдения, рационализируется в ретроспективе. Теория черных лебедей является эпистемологической , относящейся к ограниченным знаниям и пониманию наблюдателя. Термин был введен и популяризирован Нассимом Талебом и был связан с такими концепциями, как тяжелые хвосты , нелинейные выплаты, ошибка модели и даже неопределенность Найта , чья терминология событий «непознаваемое неизвестное» была популяризирована бывшим министром обороны США Дональдом Рамсфелдом. Талеб утверждает, что события черного лебедя непредсказуемы, и на практике теория призывает «готовиться, а не предсказывать» и ограничивать свою подверженность экстремальным колебаниям.

Концепция черного лебедя важна и представляет собой обоснованную критику людей, фирм и обществ, которые безответственны в том смысле, что они чрезмерно уверены в своей способности предвидеть и управлять рисками. Однако утверждение, что экстремальные события — в целом — непредсказуемы, может также привести к отсутствию ответственности в ролях управления рисками. Фактически, известно, что в широком диапазоне физических систем экстремальные события в некоторой степени предсказуемы. [4] [5] [2] [3] Нужно просто иметь достаточно глубокое понимание структуры и динамики фокальной системы и способность контролировать ее. Это область королей-драконов. Такие события были названы Талебом «серыми лебедями». Более строгое различие между черными лебедями, серыми лебедями и королями-драконами сложно, поскольку черные лебеди не определены точно в физических и математических терминах. Однако техническая проработка концепций в книге «Черный лебедь» подробно изложена в документе «Молчаливый риск». Анализ точного определения черного лебедя в контексте управления рисками был написан профессором Терье Авеном. [6]

За пределами степенных законов

5000 крупнейших просадок для 8 различных фьючерсных контрактов, построенных в соответствии с их эмпирической CCDF , сдвинутой на коэффициент 10 для наглядности. Пунктирные линии — это подгонки по степенному закону. [7]

Хорошо известно, что многие явления как в естественных, так и в социальных науках имеют статистику степенного закона ( распределение Парето ). [8] [9] [10] Кроме того, из теории экстремальных значений известно, что широкий спектр распределений (класс Фреше) имеет хвосты, которые являются асимптотически степенными. Результатом этого является то, что при работе с кризисами и экстремумами хвосты степенного закона являются «нормальным» случаем. Уникальным свойством степенных законов является то, что они масштабно-инвариантны , самоподобны и фрактальны . Это свойство подразумевает, что все события — как большие, так и малые — генерируются одним и тем же механизмом, и, таким образом, не будет никаких отдельных предшественников, по которым можно было бы предсказать самые крупные события. Хорошо известная концептуальная структура для событий этого типа — самоорганизованная критичность . Такие концепции совместимы с теорией черного лебедя. Однако Талеб также заявил, что рассмотрение степенного закона в качестве модели вместо модели с более легкими хвостами (например, гауссовой ) «превращает черных лебедей в серых», в том смысле, что модель степенного закона придает крупным событиям немалую вероятность.

В различных исследованиях было обнаружено, что, несмотря на то, что степенной закон хорошо моделирует хвост эмпирического распределения, самые крупные события значительно выпадают (т. е. намного больше, чем можно было бы ожидать в рамках модели). [7] [11] [12] Такие события интерпретируются как короли драконов, поскольку они указывают на отход от общего процесса, лежащего в основе степенного закона. Примерами этого являются самые крупные выбросы радиации, происходящие при авариях на атомных электростанциях, самый большой город (агломерация) в выборке городов страны, самые крупные крахи на финансовых рынках и внутридневные оптовые цены на электроэнергию. [7] [13]

Механизмы

Бифуркация складок в экологии [14]

С физической точки зрения, короли-драконы могут быть связаны с изменениями режимов, бифуркациями и точками невозврата сложных неравновесных систем. [1] Например, катастрофа ( бифуркация складок ) глобальной экологии, показанная на рисунке, может считаться королем-драконом: Многие наблюдатели были бы удивлены столь резким изменением состояния. Однако хорошо известно, что в динамических системах существует множество предшественников, когда система приближается к катастрофе.

Положительная обратная связь также является механизмом, который может порождать королей драконов. Например, в паническом бегстве количество бегущего скота увеличивает уровень паники, что заставляет больше скота бежать, и так далее. В человеческой динамике такое стадное и стадное поведение также наблюдалось в толпах, на фондовых рынках и так далее (см. стадное поведение ). Роль циклов положительной обратной связи в формировании короля драконов хорошо документирована, особенно в колебательных и каскадных сетях. Такая система периодически достигает точки невозврата, становясь нестабильной и запуская самоусиливающийся каскад каскадов, что приводит к королю драконов. [15]

Слева: Иллюстрация траектории системы вблизи события всплытия. Справа: эмпирическая pdf (гистограмма) пиковых высот траекторий в двойной логарифмической шкале [16]

Короли драконов также вызваны пузырением аттрактора в связанных системах осцилляторов . [16] Пузырьки аттрактора - это общее поведение, появляющееся в сетях связанных осцилляторов, где система обычно вращается в инвариантном многообразии с хаотическим аттрактором (где траектории пиков низкие), но периодически выталкивается (шумом) в область, где орбиты локально отталкиваются от инвариантного многообразия (где траектории пиков большие). Эти отклонения формируют королей драконов, как показано на рисунке. Утверждается, что такие модели могут описывать многие реальные явления, такие как землетрясения, мозговая активность и т. д. [16] Механическая модель блока и пружины, рассматриваемая как модель геологических разломов и их динамики землетрясений, дала похожее распределение. [17]

Также может быть так, что короли драконов создаются в результате системного контроля или вмешательства. То есть, попытка подавить высвобождение стресса или смерть в динамических сложных системах может привести к накоплению стресса или созреванию в сторону нестабильности. Например, лесные пожары являются естественным явлением во многих областях. Такие пожары неудобны, и поэтому мы можем желать, чтобы они были старательно потушены. Это приводит к длительным периодам без неудобных пожаров, однако , при отсутствии пожаров, накапливается мертвая древесина. Как только это накопление достигает критической точки, и начинается пожар, пожар становится настолько большим, что его невозможно контролировать — единичное событие, которое можно считать королем драконов. Другие политики, такие как ничего не делать (позволяя небольшим пожарам возникать естественным образом) или проведение стратегически контролируемого сжигания , позволят избежать огромных пожаров, допуская частые небольшие пожары. Другим примером является денежно-кредитная политика . Программы количественного смягчения и политика низких процентных ставок являются обычным явлением, направленным на предотвращение рецессий, содействие росту и т. д. Однако такие программы создают нестабильность, увеличивая неравенство доходов, поддерживая слабые компании и раздувая пузыри активов. [18] [19] В конечном итоге такая политика, направленная на сглаживание экономических колебаний, позволит осуществить колоссальную коррекцию — короля драконов.

Таксономия королей драконов. [20] Примеры систем включают:
A: Размеры городов
B: Модель инокуляции [21]
C: Сложная модель заражения [21]
D: Квазикритические нейронные модели [22] , рисовая куча [23]
E: BTW–Kuramoto [15] , Облегченная песчаная куча [24]

Как обсуждалось в предыдущем разделе, короли драконов часто возникают в системах, где другие события следуют распределению степенного закона . Механизмы, генерирующие степенные законы, хорошо изучены в рамках самоорганизованной критичности (SOC). Многие системы, демонстрирующие королей драконов наряду со степенными законами, можно понять по тому, как их динамика отличается от чистой SOC. [20] SOC обычно включает самоорганизацию (SO) вокруг непрерывного фазового перехода поглощающего состояния (ASPT), где SO относится к возникающему балансу между внешним управлением и внутренней диссипацией, а ASPT отмечает переход между активной и неактивной (поглощающей) фазами. Если этот фазовый переход является переходом первого порядка (прерывистым), он производит гистерезис, что приводит к крупным событиям короля драконов. [25] [26] Даже непрерывные переходы, которые обычно приводят к SOC, могут входить в режимы, которые производят королей драконов, в зависимости от нюансов управления и диссипации. [20] Рисунок справа иллюстрирует таксономию королей драконов, основанную на этой классификации: набор A включает всех королей драконов, в то время как наборы B и C различают тех, у кого самоорганизация близка к непрерывным и прерывистым переходам. Наборы D и E далее фокусируются на случаях со специфическими переходами поглощающего состояния.

Короли драконов как статистические выбросы

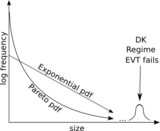
Схема функции плотности вероятности, где режим короля драконов представлен куском массы глубоко в хвосте

Короли драконов являются выбросами по определению. Однако при названии DK выбросами есть важное условие: в стандартной статистике выбросы обычно являются ошибочными значениями и отбрасываются, или выбираются статистические методы, которые каким-то образом нечувствительны к выбросам. Напротив, DK являются выбросами, которые являются высокоинформативными и должны быть в центре внимания статистического анализа. Таким образом, первым шагом является выявление DK в исторических данных. Существующие тесты основаны либо на асимптотических свойствах эмпирической функции распределения (EDF) [13] , либо на предположении о базовой кумулятивной функции распределения (CDF) данных. [7]

Оказывается, что тестирование на выбросы относительно экспоненциального распределения является очень общим. Последнее следует из теоремы Пикандса–Балкемы–де Хаана о теории экстремальных значений , которая гласит, что широкий диапазон распределений асимптотически (выше высоких порогов) имеет экспоненциальные или степенные хвосты. Кстати, это одно из объяснений, почему хвосты степенного закона так распространены при изучении экстремумов. Чтобы закончить пункт, поскольку натуральный логарифм хвоста степенного закона является экспоненциальным, можно взять логарифм данных степенного закона, а затем протестировать на выбросы относительно экспоненциального хвоста. Существует множество тестовых статистик и методов для тестирования на выбросы в экспоненциальной выборке. Внутренний тест последовательно проверяет самую большую точку, затем вторую по величине и так далее, пока первый тест не будет отклонен (т. е. нулевая гипотеза о том, что точка не является выбросом, не будет отклонена). Количество отклоненных тестов определяет количество выбросов. Например, где — отсортированная выборка, внутренний надежный тест использует статистику теста , где r — проверяемая точка , а m — заранее заданное максимальное количество выбросов. На каждом шаге должно быть вычислено p-значение для статистики теста , и если оно ниже некоторого уровня, тест отклоняется. Этот тест имеет много желательных свойств: он не требует указания количества выбросов, он не склонен к недооценке (маскировке) и переоценке (затоплению) количества выбросов, его легко реализовать, и тест не зависит от значения параметра экспоненциального хвоста. [7] х ( 1 ) > х ( 2 ) > ⋯ > х ( н ) {\displaystyle x_{(1)}>x_{(2)}>\cdots >x_{(n)}} Т г , м = х ( г ) / ( х ( м ) + ⋯ + х ( н ) ) {\displaystyle T_{r,m}=x_{(r)}/(x_{(m)}+\cdots +x_{(n)})} ( г = 1 , 2 , 3 , … ) {\displaystyle (r=1,2,3,\ldots)} г < м < н {\displaystyle r<m<n}

Примеры

(II) Эмпирическая CCDF логарифма выброса радиации (серый пунктир) и ущерба (черный), вызванного авариями на атомных электростанциях, со сплошными линиями, дающими подобранный хвост степенного закона. (III) Эмпирическая CCDF населения в городских агломерациях внутри страны, масштабированная таким образом, что вторая по величине имеет размер 1. Выбросы помечены. [7]

Вот несколько примеров, когда короли-драконы были обнаружены как исключения: [7] [13]

  • финансовые крахи, измеряемые спадами , где выбросы соответствуют террористическим атакам (например, взрыву в Лондоне в 2005 году ) и внезапному краху 2010 года ;
  • выбросы радиации и финансовые потери, вызванные авариями на атомных электростанциях, где выбросы соответствуют неконтролируемым катастрофам, когда механизмы безопасности вышли из строя;
  • крупнейший город (по численности населения в его агломерации) среди населения городов страны, где крупнейший город играет непропорционально важную роль в динамике страны и выигрывает от уникального роста;
  • внутридневные оптовые цены на электроэнергию; и
  • трехволновое нелинейное взаимодействие — возможно подавление появления королей-драконов. [27]

Моделирование и прогнозирование

Предсказуемость, основанная на взаимодействии и разнообразии в системе [28]

То, как моделировать и предсказывать драконьих королей, зависит от лежащего в основе механизма. Однако общий подход потребует постоянного мониторинга фокальной системы и сравнения измерений с ( нелинейной или сложной ) динамической моделью. Было высказано предположение, что чем более однородна система и чем сильнее ее взаимодействия, тем более предсказуемой она будет. [28]

Моделирование и прогнозирование пузыря (суперэкспоненциального роста) с помощью логопериодического степенного закона [29]

Например, в нелинейных системах с фазовыми переходами в критической точке хорошо известно, что окно предсказуемости возникает в окрестности критической точки из-за предшествующих признаков: система медленнее восстанавливается после возмущений, изменяется автокорреляция, увеличивается дисперсия, увеличивается пространственная когерентность и т. д. [30] [31] Эти свойства использовались для прогнозирования во многих приложениях, начиная от изменений в биосфере [14] и заканчивая разрывом резервуаров высокого давления на ракете Ariane. [32] Приложения к широкому спектру явлений стимулировали перспективу сложных систем, которая является трансдисциплинарным подходом и не зависит от понимания первых принципов.

Четыре режима просмотров видео YouTube в день. [33]

Для явлений неустойчивого роста (например, населения или цен на акции) можно рассмотреть модель роста, которая характеризуется конечной временной сингулярностью, которая является критической точкой, где режим роста изменяется. В системах, которые являются дискретно масштабно-инвариантными, такая модель представляет собой рост по степенному закону, украшенный логопериодической функцией. [34] [35] Подгонка этой модели к данным о росте ( нелинейная регрессия ) позволяет предсказать сингулярность, т. е. конец неустойчивого роста. Это применялось ко многим проблемам, [3] например: разрыв материалов, [32] [36] землетрясения, [37] и рост и взрыв пузырей на финансовых рынках [12] [38] [39] [40] [41]

Интересной динамикой для рассмотрения, которая может раскрыть развитие успеха блокбастера, являются эпидемические явления : например, распространение чумы, вирусные явления в СМИ, распространение паники и волатильности на фондовых рынках и т. д. В таком случае эффективным подходом является разложение активности/колебаний на экзогенные и эндогенные части и изучение эндогенной динамики, которая может привести к весьма влиятельным всплескам активности. [33] [42] [43]

Прогнозирование и принятие решений

При наличии модели и данных можно получить статистическую оценку модели. Затем эту оценку модели можно использовать для вычисления интересных величин, таких как условная вероятность появления события «король драконов» в будущем временном интервале и наиболее вероятное время появления. При статистическом моделировании экстремальных значений и использовании сложных или нелинейных динамических моделей обязательно будет существенная неопределенность. Таким образом, следует быть внимательным в количественной оценке неопределенности: не только принимая во внимание случайность, присутствующую в подобранной стохастической модели, но и неопределенность ее оценочных параметров (например, с помощью байесовских методов или сначала моделируя параметры, а затем моделируя из модели с этими параметрами), а также неопределенность в выборе модели (например, рассматривая ансамбль различных моделей).

Затем можно использовать оцененные вероятности и связанные с ними неопределенности для принятия решений. В простейшем случае выполняется бинарная классификация : прогнозирование того, что король драконов появится в будущем интервале, если вероятность его появления достаточно высока, с достаточной уверенностью. Например, можно предпринять определенные действия, если прогнозируется появление короля драконов. Оптимальное решение затем сбалансирует стоимость ложных отрицательных / ложных положительных результатов и промахов / ложных тревог в соответствии с заданной функцией потерь . Например, если стоимость промаха очень велика по сравнению со стоимостью ложной тревоги, оптимальное решение будет обнаруживать королей драконов чаще, чем они появляются. Также следует изучить истинно положительную частоту прогноза. Чем меньше это значение, тем слабее тест и тем ближе он к территории черного лебедя. На практике выбор оптимального решения и вычисление его свойств должны выполняться путем перекрестной проверки с историческими данными (если они доступны) или на смоделированных данных (если известно, как смоделировать королей драконов).

В динамической обстановке набор данных будет расти со временем, а оценка модели и ее предполагаемые вероятности будут меняться. Затем можно рассмотреть возможность объединения последовательности оценок/вероятностей при выполнении прогнозирования. В этой динамической обстановке тест, скорее всего, будет слабым большую часть времени (например, когда система находится около равновесия), но по мере приближения к королю драконов и появления видимых предшественников истинно положительный показатель должен увеличиваться.

Важность экстремальных рисков

Короли драконов формируют особые виды событий, ведущих к экстремальным рискам (которые также могут быть возможностями). Что экстремальные риски важны и должны быть очевидны. Стихийные бедствия дают много примеров (например, падение астероидов, приводящее к вымиранию). Вот некоторые статистические примеры влияния экстремальных ситуаций: крупнейшая авария на атомной электростанции ( катастрофа в Чернобыле ) имела примерно такую ​​же стоимость ущерба (измеряемую по оценочной стоимости в долларах США), как и все (+- 175) другие исторические ядерные аварии вместе взятые, [44] крупнейшие 10 процентов утечек личных данных организаций составляют 99 процентов от общего объема утечек личной информации, [45] крупнейшие пять эпидемий с 1900 года вызвали в 20 раз больше смертей, чем оставшиеся 1363, [7] [46] и т. д. В целом такая статистика появляется при наличии распределений с тяжелыми хвостами , и присутствие королей драконов увеличит и без того чрезмерно большой эффект экстремальных ситуаций.

Несмотря на важность экстремальных событий, из-за невежества, несогласованных стимулов и когнитивных предубеждений часто происходит неспособность адекватно предвидеть их. Технически говоря, это приводит к плохо определенным моделям, где распределения недостаточно тяжелые хвосты, и недооценивают как последовательную, так и многомерную зависимость экстремальных событий. Некоторые примеры таких неудач в оценке рисков включают использование гауссовых моделей в финансах ( Блэк-Шоулз , гауссовская копула, LTCM ), использование гауссовых процессов и линейной волновой теории, неспособных предсказать возникновение волн-убийц , неспособность экономических моделей в целом предсказать финансовый кризис 2007–2008 годов и недооценку внешних событий, каскадов и нелинейных эффектов в вероятностной оценке риска , что привело к непредвидению ядерной катастрофы на Фукусиме в 2011 году. Такие влиятельные неудачи подчеркивают важность изучения экстремальных событий.

Управление рисками

Концепция короля драконов поднимает много вопросов о том, как можно справиться с риском. Конечно, если возможно, следует избегать подверженности большим рискам (часто называемой «методом черного лебедя»). Однако во многих разработках подверженность риску является необходимостью, и необходимо найти компромисс между риском и доходностью.

В адаптивной системе, где предсказание драконьих королей успешно, можно действовать, чтобы защитить систему или даже получить прибыль. Как спроектировать такие устойчивые системы , а также их системы мониторинга рисков в реальном времени, [47] является важной и междисциплинарной проблемой, где драконьи короли должны быть рассмотрены.

С другой стороны, когда дело доходит до количественной оценки риска в данной системе (будь то банк, страховая компания, плотина, мост или социально-экономическая система), риск необходимо учитывать за период, например, ежегодно. Обычно интересуют такие статистические данные, как годовая вероятность потерь или ущерба, превышающих некоторую величину ( стоимость риска ), другие меры хвостового риска и периоды возврата . Чтобы предоставить такие характеристики риска, динамические короли драконов должны быть обоснованы с точки зрения годовой статистики частоты и серьезности. Затем эти статистики частоты и серьезности можно объединить в модель, например, составной процесс Пуассона .

При условии, что статистические свойства системы постоянны во времени (стационарны), статистика частоты и серьезности может быть построена на основе прошлых наблюдений, моделирования и/или предположений. Если нет, можно только построить сценарии. Однако в любом случае, учитывая существующую неопределенность, следует рассмотреть ряд сценариев. Из-за нехватки данных для экстремальных событий, принципа экономии и теоретических результатов теории экстремальных значений об универсальных моделях хвоста, обычно полагаются на обобщенную модель хвоста распределения Парето ( GPD ). Однако такая модель исключает DK. Таким образом, когда есть достаточные основания полагать, что присутствуют короли-драконы, или если просто хочется рассмотреть сценарий, можно, например, рассмотреть смесь плотности GPD и плотности для режима DK.

Ссылки

  1. ^ abc Sornette, Didier и Guy Ouillon. «Короли-драконы: механизмы, статистические методы и эмпирические данные». The European Physical Journal Special Topics 205.1 (2012): 1–26.
  2. ^ ab D. Sornette, Короли-драконы, черные лебеди и прогнозирование кризисов, Международный журнал науки и техники Terraspace 1(3), 1–17 (2009) (https://arxiv.org/abs/0907.4290) и (http://ssrn.com/abstract=1470006)
  3. ^ abc D. Sornette, Предсказуемость катастрофических событий: материальный разрыв, землетрясения, турбулентность, финансовые крахи и рождение человека, Proc. Natl. Acad. Sci. USA 99, SUPP1 (2002), 2522–2529.
  4. ^ Sornette, Didier (17 июня 2013 г.). «Как мы можем предсказать следующий финансовый кризис» . Получено 11 ноября 2021 г. – через www.ted.com.
  5. ^ Альбеверио, Серджио, Фолькер Йентч и Хольгер Канц. Экстремальные явления в природе и обществе. Springer Science & Business Media, 2006.
  6. ^ Авен, Терье. «О значении черного лебедя в контексте риска». Safety science 57 (2013): 44–51.
  7. ^ abcdefgh Уитли, Спенсер и Дидье Сорнетт. «Обнаружение множественных выбросов в выборках с экспоненциальными и Парето-хвостами: освобождение от внутреннего подхода и обнаружение королей-драконов». Препринт arXiv arXiv:1507.08689 (2015).
  8. ^ Митценмахер, Майкл. «Краткая история генеративных моделей для степенного закона и логнормальных распределений». Интернет-математика 1.2 (2004): 226–251.
  9. ^ Ньюман, Марк Э.Дж. «Степенные законы, распределения Парето и закон Ципфа». Contemporary physics 46.5 (2005): 323–351.
  10. ^ Сорнетт, Дидье. «Критические явления в естественных науках: хаос, фракталы, самоорганизация и беспорядок: концепции и инструменты (серия Springer по синергетике)». (2006).
  11. ^ Писаренко, В. Ф. и Д. Сорнетт. «Надежные статистические тесты драконов-королей за пределами степенных распределений». The European Physical Journal Special Topics 205.1 (2012): 95–115.
  12. ^ Аб Йохансен, Андерс и Дидье Сорнетт. «Потрясения, крахи и пузыри на финансовых рынках». Обзор экономики Брюсселя (Cahiers economiques de Bruxelles) 53.2 (2010): 201–253.
  13. ^ abc Janczura, J.; Weron, R. (2012). «Черные лебеди или короли-драконы? Простой тест на отклонения от степенного закона». The European Physical Journal Special Topics . 205 (1): 79– 93. arXiv : 1102.3712 . Bibcode :2012EPJST.205...79J. doi :10.1140/epjst/e2012-01563-9. ISSN  1951-6355. S2CID  52260499.
  14. ^ ab Барноски, Энтони Д. и др. «Приближение изменения состояния биосферы Земли». Nature 486.7401 (2012): 52–58.
  15. ^ ab Микаберидзе, Гурам; Д'Соуза, Раисса М. (2022-05-01). "Каскады из песчаных куч в сетях осцилляторов: модель BTW встречает модель Курамото". Хаос: междисциплинарный журнал нелинейной науки . 32 (5). doi : 10.1063/5.0095094. ISSN  1054-1500. PMID  35649989.
  16. ^ abc Кавальканте, Хьюго Л. Д. де С. и др. «Предсказуемость и подавление экстремальных событий в хаотической системе». Physical review letters 111.19 (2013): 198701.
  17. ^ Шоу, Брюс Э., Джин М. Карлсон и Джеймс С. Лангер. «Закономерности сейсмической активности, предшествующие крупным землетрясениям». Журнал геофизических исследований: Solid Earth (1978–2012) 97.B1 (1992): 479–488.
  18. ^ Сорнетт, Дидье и Питер Коуэлс. «1980–2008: Иллюзия вечной денежной машины и что она сулит в будущем». Риски 2.2 (2014): 103–131.
  19. ^ Сорнетт, Дидье и Питер Коуэлс. «Управление рисками в жутком мире». Журнал управления рисками в финансовых учреждениях 8.1 (2015): 83–108.
  20. ^ abc Микаберидзе, Гурам; Плауд, Артур; Д'Соуза, Раисса М. (2023-10-19). "Короли драконов в самоорганизованных системах критичности". Physical Review Research . 5 (4). arXiv : 2308.02658 . doi : 10.1103/PhysRevResearch.5.L042013. ISSN  2643-1564.
  21. ^ Аб Линь, Юаньшэн; Бургхардт, Кейт; Роден, Мартин; Ноэль, Пьер-Андре; Д'Суза, Раиса М. (27 августа 2018 г.). «Самоорганизация неудач короля драконов». Физический обзор E . 98 (2): 022127.arXiv : 1705.10831 . doi : 10.1103/physreve.98.022127. ISSN  2470-0045. ПМИД  30253566.
  22. ^ Киноучи, Осаме; Брокини, Людмила; Коста, Ариадна А.; Кампос, Жоау Гильерме Феррейра; Копелли, Мауро (07.03.2019). «Стохастические колебания и лавины короля драконов в самоорганизующихся квазикритических системах». Научные отчеты . 9 (1): 3874. doi : 10.1038/s41598-019-40473-1. ISSN  2045-2322. ПМК 6405991 . ПМИД  30846773. 
  23. ^ Амарал, Луис А. Нунес; Лауритсен, Кент Бекгор (1996-11-01). «Самоорганизованная критичность в модели рисовой кучи». Physical Review E . 54 (5): R4512 – R4515 . arXiv : cond-mat/9610010 . doi :10.1103/physreve.54.r4512. ISSN  1063-651X. PMID  9965793.
  24. ^ Ди Санто, Серена; Буриони, Раффаэлла; Веццани, Алессандро; Муньос, Мигель А. (2016-06-13). «Самоорганизованная бистабильность, связанная с фазовыми переходами первого порядка». Physical Review Letters . 116 (24): 240601. arXiv : 1605.05161 . doi :10.1103/physrevlett.116.240601. ISSN  0031-9007. PMID  27367373.
  25. ^ Ди Санто, Серена; Буриони, Раффаэлла; Веццани, Алессандро; Муньос, Мигель А. (2016-06-13). «Самоорганизованная бистабильность, связанная с фазовыми переходами первого порядка». Physical Review Letters . 116 (24): 240601. arXiv : 1605.05161 . doi :10.1103/physrevlett.116.240601. ISSN  0031-9007. PMID  27367373.
  26. ^ Буэндиа, Виктор; ди Санто, Серена; Вильегас, Пабло; Буриони, Рафаэлла; Муньос, Мигель А. (16 марта 2020 г.). «Самоорганизованная бистабильность и ее возможное значение для динамики мозга». Обзор физических исследований . 2 (1): 013318. arXiv : 1911.05382 . doi : 10.1103/physrevresearch.2.013318. ISSN  2643-1564.
  27. ^ Виана, Рикардо Л.; Кальдас, Ибере Л.; Ярош, Келли С.; Батиста, Антонио М.; Сезек-младший, Хосе Д.; Сантос, Мойзес С. (1 мая 2019 г.). «Смерть королей-драконов в нелинейных волновых взаимодействиях». Физика А: Статистическая механика и ее приложения . 534 : 122296. arXiv : 1905.00528 . Бибкод : 2019PhyA..53422296S. doi :10.1016/j.physa.2019.122296. S2CID  143424915.
  28. ^ ab Sornette, D., P. Miltenberger и C. Vanneste. "Статистическая физика структур разломов, самоорганизованных повторяющимися землетрясениями: синхронизация против самоорганизованной критичности". Recent Progresses in Statistical Mechanics and Quantum Field Theory (World Scientific, Сингапур, 1995) (1994): 313–332.
  29. ^ Сорнетт, Дидье, Райан Вудард и Вэй-Син Чжоу. «Нефтяной пузырь 2006–2008 гг.: доказательства спекуляций и прогнозов». Physica A: Статистическая механика и ее приложения 388.8 (2009): 1571–1576.
  30. ^ Строгац, Стивен Х. Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике. Westview press, 2014
  31. ^ Шеффер, Мартен и др. «Предвосхищение критических переходов». Science 338.6105 (2012): 344–348.
  32. ^ ab J.-C. Anifrani, C. Le Floc'h, D. Sornette и B. Souillard, Универсальная логопериодическая поправка к масштабированию ренормгруппы для прогнозирования напряжения разрыва по акустической эмиссии, J.Phys.I France 5 (6) (1995): 631–638.
  33. ^ ab Крейн, Райли и Дидье Сорнетт. «Надежные динамические классы, выявленные путем измерения функции отклика социальной системы». Труды Национальной академии наук 105.41 (2008): 15649–15653.
  34. ^ Сорнетт, Дидье. «Инвариантность дискретного масштаба и комплексные размерности». Physics reports 297.5 (1998): 239–270.
  35. ^ Хуан, И., Уйон, Г., Салеур, Х. и Сорнетт, Д. (1997). Спонтанное возникновение дискретной масштабной инвариантности в моделях роста. Physical Review E, 55(6), 6433.
  36. ^ А. Йохансен и Д. Сорнетт, Критические разрывы, Eur. Phys. J. B 18 (2000): 163–181.
  37. ^ SG Sammis и D. Sornette, Положительная обратная связь, память и предсказуемость землетрясений, Труды Национальной академии наук США 99 SUPP1 (2002): 2501–2508.
  38. ^ Сорнетт, Дидье, Андерс Йохансен и Жан-Филипп Бушо. «Обвалы фондового рынка, предшественники и копии». Journal de Physique I 6.1 (1996): 167–175.
  39. ^ Фейгенбаум, Джеймс А. и Питер ГО Фройнд. «Дискретная масштабная инвариантность на фондовых рынках перед крахами». Международный журнал современной физики B 10.27 (1996): 3737–3745.
  40. ^ Сорнетт, Дидье и др. «Пояснения к вопросам и критике модели финансового пузыря Йохансена–Ледуа–Сорнетта». Physica A: Statistical Mechanics and its Applications 392.19 (2013): 4417–4428.
  41. ^ "Financial Crisis Observatory". er.ethz.ch . Получено 11 ноября 2021 г. .
  42. ^ Sornette, Didier (2006). «Эндогенные и экзогенные истоки кризисов (экстремальные события в природе и обществе) | Springer Berlin Heidelberg». стр.  95–119 . arXiv : physics/0412026 .
  43. ^ Филимонов, Владимир и Дидье Сорнетт. «Количественная оценка рефлексивности на финансовых рынках: к прогнозированию внезапных крахов». Physical Review E 85.5 (2012): 056108.
  44. ^ Уитли, Спенсер, Бенджамин Совакул и Дидье Сорнетт. «О катастрофах и королях-драконах: статистический анализ инцидентов и аварий на атомных электростанциях». Препринт arXiv arXiv:1504.02380 (2015).
  45. ^ Уитли, Спенсер, Томас Майлларт и Дидье Сорнетт. «Чрезвычайный риск утечки персональных данных и эрозия конфиденциальности». Препринт arXiv arXiv:1505.07684 (2015).
  46. ^ Гуха-Сапир, Д., Р. Белу и Ф. Хойоис. «EM-DAT: Международная база данных катастроф». Католический университет Лувена, Брюссель: Бельгия. www. em-dat. net. (2014).
  47. ^ Сорнетт, Дидье и Татьяна Коваленко. «Динамическая диагностика и решения для устойчивых природных и социальных систем». Planet@ Risk 1 (1) (2013) 7–33.
Взято с "https://en.wikipedia.org/w/index.php?title=Теория_короля_дракона&oldid=1257432035"