Двусторонняя приоритетная очередь
В информатике двухсторонняя приоритетная очередь (DEPQ) [1] или двухсторонняя куча [2] — это структура данных , похожая на приоритетную очередь или кучу , но позволяющая эффективно удалять как максимум, так и минимум, в соответствии с некоторым порядком ключей ( элементов), хранящихся в структуре. Каждый элемент в DEPQ имеет приоритет или значение. В DEPQ можно удалять элементы как в порядке возрастания, так и в порядке убывания. [3]
Операции
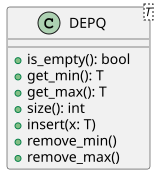
Двусторонняя приоритетная очередь включает в себя следующие операции:
- isEmpty()
- Проверяет, пуст ли DEPQ, и возвращает true, если пуст.
- размер()
- Возвращает общее количество элементов, присутствующих в DEPQ.
- получитьМин()
- Возвращает элемент с наименьшим приоритетом.
- получитьМакс()
- Возвращает элемент с наивысшим приоритетом.
- положить( х )
- Вставляет элемент x в DEPQ.
- удалитьМин()
- Удаляет элемент с минимальным приоритетом и возвращает этот элемент.
- удалитьМакс()
- Удаляет элемент с максимальным приоритетом и возвращает этот элемент.
Кроме того, приоритет любого элемента может быть изменен после его вставки в DEPQ. [4]
Выполнение
Двусторонние очереди с приоритетами могут быть построены из сбалансированных двоичных деревьев поиска (где минимальным и максимальным элементами являются крайние левые и правые листья соответственно) или с использованием специализированных структур данных, таких как куча минимума-максимума и куча пар .
Общие методы перехода от обычных очередей к двухсторонним приоритетным очередям: [5]
Метод двойной структуры

В этом методе поддерживаются две разные очереди приоритетов для min и max. Те же элементы в обеих PQ показаны с помощью указателей соответствия.
Здесь минимальными и максимальными элементами являются значения, содержащиеся в корневых узлах min heap и max heap соответственно.
- Удаление минимального элемента : выполните removemin() для минимальной кучи и remove( значение узла ) для максимальной кучи, где значение узла — это значение в соответствующем узле в максимальной куче.
- Удаление максимального элемента : выполните removemax() для максимальной кучи и remove( значение узла ) для минимальной кучи, где значение узла — это значение в соответствующем узле в минимальной куче.
Полная переписка

Половина элементов находится в min PQ, а другая половина — в max PQ. Каждый элемент в min PQ имеет однозначное соответствие с элементом в max PQ. Если количество элементов в DEPQ нечетное, один из элементов сохраняется в буфере. [1] Приоритет каждого элемента в min PQ будет меньше или равен соответствующему элементу в max PQ.
Листовая переписка

В отличие от полного соответствия, в этом методе только конечные элементы минимального и максимального PQ образуют соответствующие пары один к одному. Неконечным элементам не обязательно находиться в паре соответствия один к одному. [1]
Если количество элементов в DEPQ нечетное, один из элементов сохраняется в буфере. [1]
Интервальные кучи

Помимо вышеупомянутых методов соответствия, DEPQ можно эффективно получить с помощью интервальных куч. [6] Интервальная куча похожа на вложенную мин-макс кучу, в которой каждый узел содержит два элемента. Это полное бинарное дерево, в котором: [6]
- Левый элемент меньше или равен правому элементу.
- Оба элемента определяют замкнутый интервал.
- Интервал, представленный любым узлом, кроме корневого, является подинтервалом родительского узла.
- Элементы с левой стороны определяют минимальную кучу .
- Элементы с правой стороны определяют максимальную кучу .
В зависимости от количества элементов возможны два случая [6] -
- Четное число элементов: В этом случае каждый узел содержит два элемента, скажем, p и q , где p ≤ q . Каждый узел тогда представлен интервалом [ p , q ].
- Нечетное количество элементов: в этом случае каждый узел, за исключением последнего, содержит два элемента, представленных интервалом [ p , q ], тогда как последний узел будет содержать один элемент и представлен интервалом [ p , p ].
Вставка элемента
В зависимости от количества элементов, уже присутствующих в интервальной куче, возможны следующие случаи:
- Нечетное количество элементов: Если количество элементов в интервальной куче нечетное, новый элемент сначала вставляется в последний узел. Затем он последовательно сравнивается с предыдущими элементами узла и проверяется на соответствие критериям, необходимым для интервальной кучи, как указано выше. В случае, если элемент не удовлетворяет ни одному из критериев, он перемещается из последнего узла в корень, пока все условия не будут выполнены. [6]
- Четное количество элементов: Если количество элементов четное, то для вставки нового элемента создается дополнительный узел. Если элемент попадает слева от родительского интервала, то он считается находящимся в минимальной куче, а если элемент попадает справа от родительского интервала, то он считается находящимся в максимальной куче . Далее последовательно сравниваются и перемещаются от последнего узла к корню, пока не будут выполнены все условия для интервальной кучи. Если элемент попадает в интервал самого родительского узла, то процесс тут же останавливается и перемещение элементов не происходит. [6]
Время, необходимое для вставки элемента, зависит от количества движений, необходимых для выполнения всех условий, и составляет O (log n ).
Удаление элемента
- Мин. элемент: В интервальной куче минимальным элементом является элемент с левой стороны корневого узла. Этот элемент удаляется и возвращается. Чтобы заполнить вакансию, созданную с левой стороны корневого узла, элемент из последнего узла удаляется и повторно вставляется в корневой узел. Затем этот элемент последовательно сравнивается со всеми левыми элементами нисходящих узлов, и процесс останавливается, когда выполняются все условия для интервальной кучи. В случае, если левый элемент в узле становится больше правого элемента на любом этапе, два элемента меняются местами [6] , а затем выполняются дальнейшие сравнения. Наконец, корневой узел снова будет содержать минимальный элемент с левой стороны.
- Максимальный элемент: В интервальной куче максимальный элемент — это элемент с правой стороны корневого узла. Этот элемент удаляется и возвращается. Чтобы заполнить вакансию, созданную с правой стороны корневого узла, элемент из последнего узла удаляется и повторно вставляется в корневой узел. Дальнейшие сравнения выполняются на аналогичной основе, как обсуждалось выше. Наконец, корневой узел снова будет содержать максимальный элемент с правой стороны.
Таким образом, с интервальными кучами как минимальные, так и максимальные элементы могут быть эффективно удалены путем перемещения от корня к листу. Таким образом, DEPQ может быть получен [6] из интервальной кучи, где элементы интервальной кучи являются приоритетами элементов в DEPQ.
Сложность времени
Интервальные кучи
При реализации DEPQ с использованием интервальных куч, состоящих из n элементов, временные сложности для различных функций сформулированы в таблице ниже [1]
| Операция | Сложность времени |
|---|---|
| инициализация() | На ) |
| isEmpty() | О (1) |
| получитьмин() | О (1) |
| получитьмакс() | О (1) |
| размер() | О (1) |
| вставить(x) | О (лог n ) |
| удалитьМин() | О (лог n ) |
| удалитьМакс() | О (лог n ) |
Сопряжение куч
При реализации DEPQ с использованием куч или парных куч, состоящих из n элементов, временные сложности для различных функций сформулированы в таблице ниже. [1] Для парных куч это амортизированная сложность .
| Операция | Сложность времени |
|---|---|
| isEmpty() | О (1) |
| получитьмин() | О (1) |
| получитьмакс() | О (1) |
| вставить(x) | О (лог n ) |
| удалитьМакс() | О (лог n ) |
| удалитьМин() | О (лог n ) |
Приложения
Внешняя сортировка
Одним из примеров применения двухсторонней очереди с приоритетом является внешняя сортировка . При внешней сортировке элементов больше, чем может храниться в памяти компьютера. Элементы, которые должны быть отсортированы, изначально находятся на диске, а отсортированная последовательность должна быть оставлена на диске. Внешняя быстрая сортировка реализуется с использованием DEPQ следующим образом:
- Считайте столько элементов, сколько поместится во внутренний DEPQ. Элементы в DEPQ в конечном итоге станут средней группой (осью) элементов.
- Считать оставшиеся элементы. Если следующий элемент ≤ наименьшего элемента в DEPQ, вывести этот следующий элемент как часть левой группы. Если следующий элемент ≥ наибольшего элемента в DEPQ, вывести этот следующий элемент как часть правой группы. В противном случае удалить максимальный или минимальный элемент из DEPQ (выбор может быть сделан случайным образом или поочередно); если максимальный элемент удален, вывести его как часть правой группы; в противном случае вывести удаленный элемент как часть левой группы; вставить новый входной элемент в DEPQ.
- Выведите элементы в DEPQ в отсортированном порядке как среднюю группу.
- Рекурсивно отсортируйте левую и правую группы.
Смотрите также
Ссылки
- ^ abcdefghi Структуры данных, алгоритмы и приложения в Java: двухсторонние очереди с приоритетами, Сартадж Сахни , 1999.
- ^ Брасс, Питер (2008). Расширенные структуры данных . Cambridge University Press. стр. 211. ISBN 9780521880374.
- ^ "Depq - Двусторонняя приоритетная очередь". Архивировано из оригинала 2012-04-25 . Получено 2011-10-04 .
- ^ "depq".
- ^ Основы структур данных в C++ - Эллис Горовиц, Сартадж Сахни и Динеш Мехта
- ^ abcdefg http://www.mhhe.com/engcs/compsci/sahni/enrich/c9/interval.pdf [ пустой URL-адрес PDF ]