Двоичная куча
| Двоичная (мин.) куча | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | двоичное дерево/куча | ||||||||||||||||||||||||||
| Изобретенный | 1964 | ||||||||||||||||||||||||||
| Изобретено | Дж. У. Дж. Уильямс | ||||||||||||||||||||||||||
| |||||||||||||||||||||||||||


Двоичная куча — это структура данных кучи , которая принимает форму двоичного дерева . Двоичные кучи являются распространенным способом реализации приоритетных очередей . [1] : 162–163 Двоичная куча была введена Дж. У. Дж. Уильямсом в 1964 году как структура данных для реализации пирамидальной сортировки . [2]
Двоичная куча определяется как двоичное дерево с двумя дополнительными ограничениями: [3]
- Свойство формы: двоичная куча представляет собой полное двоичное дерево ; то есть все уровни дерева, за исключением, возможно, последнего (самого глубокого), полностью заполнены, и, если последний уровень дерева не заполнен, узлы этого уровня заполняются слева направо.
- Свойство кучи: ключ, хранящийся в каждом узле, либо больше или равен (≥), либо меньше или равен (≤) ключам в дочерних узлах, в соответствии с некоторым общим порядком .
Кучи, где родительский ключ больше или равен (≥) дочерним ключам, называются max-heaps ; те, где он меньше или равен (≤), называются min-heaps . Эффективные (то есть логарифмические по времени ) алгоритмы известны для двух операций, необходимых для реализации приоритетной очереди на двоичной куче:
- Вставка элемента;
- Удаление наименьшего или наибольшего элемента из (соответственно) min-heap или max-heap.
Двоичные кучи также обычно используются в алгоритме сортировки пирамидальной сортировки , который является алгоритмом на месте, поскольку двоичные кучи могут быть реализованы как неявная структура данных , сохраняющая ключи в массиве и использующая их относительные положения внутри этого массива для представления отношений «потомок-родитель».
Операции с кучей
Обе операции — вставка и удаление — сначала изменяют кучу, чтобы сохранить свойство формы, добавляя или удаляя с конца кучи. Затем свойство кучи восстанавливается путем перемещения вверх или вниз по куче. Обе операции занимают время O(log n ) .
Вставлять
Чтобы вставить элемент в кучу, мы выполняем следующие шаги:
- Добавьте элемент на нижний уровень кучи в самое левое открытое пространство.
- Сравните добавленный элемент с его родителем; если они в правильном порядке, остановитесь.
- Если нет, поменяйте местами элемент с его родительским и вернитесь к предыдущему шагу.
Шаги 2 и 3, которые восстанавливают свойство кучи путем сравнения и возможной замены узла на его родительский узел, называются операцией up-heap (также известной как bubble-up , percolate-up , sift-up , trickle-up , swim-up , heapify-up , cascade-up или fix-up ).
Количество требуемых операций зависит только от количества уровней, на которые должен подняться новый элемент, чтобы удовлетворить свойству кучи. Таким образом, операция вставки имеет наихудшую временную сложность O(log n ) . Для случайной кучи и для повторных вставок операция вставки имеет среднюю временную сложность O(1). [4] [5]
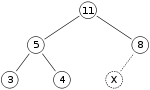
В качестве примера вставки двоичной кучи предположим, что у нас есть максимальная куча
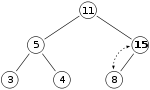
и мы хотим добавить в кучу число 15. Сначала мы помещаем 15 в позицию, отмеченную X. Однако свойство кучи нарушается, поскольку 15 > 8 , поэтому нам нужно поменять местами 15 и 8. Итак, после первой замены куча выглядит следующим образом:
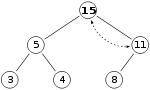
Однако свойство кучи все еще нарушается, поскольку 15 > 11 , поэтому нам нужно снова выполнить замену:
что является допустимой max-heap. Нет необходимости проверять левого потомка после этого последнего шага: в начале max-heap был допустимым, то есть корень уже был больше своего левого потомка, поэтому замена корня еще большим значением сохранит свойство, что каждый узел больше своих потомков ( 11 > 5 ; если 15 > 11 и 11 > 5 , то 15 > 5 из-за транзитивного отношения ).
Извлекать
Процедура удаления корня из кучи (фактически извлечение максимального элемента в max-куче или минимального элемента в min-куче) с сохранением свойства кучи выглядит следующим образом:
- Замените корень кучи последним элементом на последнем уровне.
- Сравните новый корень с его дочерними элементами; если они расположены в правильном порядке, остановитесь.
- Если нет, поменяйте элемент с одним из его дочерних элементов и вернитесь к предыдущему шагу. (Поменяйте местами его меньший дочерний элемент в минимальной куче и его больший дочерний элемент в максимальной куче.)
Шаги 2 и 3, которые восстанавливают свойство кучи путем сравнения и возможной замены узла на один из его дочерних узлов, называются операцией down-heap (также известной как bubble-down , percolate-down , sift-down , sink-down , trickle down , heapify-down , cascade-down , fix-down , extract-min или extract-max или просто heapify ).
Итак, если у нас та же максимальная куча, что и раньше
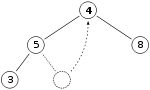
Удаляем 11 и заменяем его на 4.
Теперь свойство кучи нарушено, поскольку 8 больше 4. В этом случае для восстановления свойства кучи достаточно поменять местами два элемента, 4 и 8, и нам не нужно менять элементы местами дальше:
Узел, движущийся вниз, меняется местами с большим из своих потомков в max-heap (в min-heap он будет меняться местами со своим меньшим потомком), пока он не удовлетворит свойству кучи в своем новом положении. Эта функциональность достигается функцией Max -Heapify , как определено ниже в псевдокоде для кучи с поддержкой массива A длины length ( A ) . A индексируется, начиная с 1.
// Выполнить операцию down-heap или heapify-down для max-heap// A : массив, представляющий кучу, индексированный начиная с 1// i : индекс, с которого следует начать при пирамидальной разбивке Max-Heapify ( A , i ): left ← 2× i right ← 2× i + 1 largest ← i если лево ≤ длина ( A ) и A [ лево ] > A [ наибольший ] тогда : наибольший ← лево
если право ≤ длина ( A ) и A [ право ] > A [ наибольший ] тогда : наибольший ← право если largest ≠ i, то : поменять местами A [ i ] и A [ largest ] Max-Heapify ( A , largest )
Для того, чтобы приведенный выше алгоритм правильно переделал массив в кучу, ни один узел, кроме узла с индексом i и его двух прямых потомков, не может нарушить свойство кучи. Операция down-heap (без предшествующего обмена) также может использоваться для изменения значения корня, даже если элемент не удаляется.
В худшем случае новый корень придется менять местами со своим дочерним элементом на каждом уровне, пока он не достигнет нижнего уровня кучи, а это означает, что операция удаления имеет временную сложность относительно высоты дерева, или O(log n ).
Вставить, затем извлечь
Вставка элемента, а затем извлечение из кучи может быть выполнено более эффективно, чем простой вызов функций вставки и извлечения, определенных выше, что включало бы как операцию, так upheapи downheapоперацию. Вместо этого мы можем выполнить только downheapоперацию, как показано ниже:
- Сравнить, больше ли элемент, который мы выдвигаем, или элемент, который находится наверху кучи (предполагая, что куча максимальная)
- Если корень кучи больше:
- Заменить корень новым элементом
- Down-heapify, начиная с корня
- В противном случае верните товар, который мы продвигаем.
Python предоставляет такую функцию для вставки, а затем извлечения, называемую «heappushpop», которая перефразирована ниже. [6] [7] Предполагается, что массив кучи имеет первый элемент с индексом 1.
// Помещаем новый элемент в (максимальную) кучу, а затем извлекаем корень полученной кучи.// куча : массив, представляющий кучу, индексированный с 1// item : элемент для вставки// Возвращает большее из двух значений между элементом и корнем кучи . Push-Pop ( heap : List<T>, item : T) -> T: если куча не пуста и heap[1] > item тогда : // < if min heap поменять местами heap [1] и item _downheap( heap, начиная с индекса 1) return item
Аналогичную функцию можно определить для извлечения и последующей вставки, что в Python называется «heapreplace»:
// Извлечь корень кучи и добавить новый элемент// куча : массив, представляющий кучу, индексированный с 1// item : элемент для вставки// Возвращает текущий корень кучи Replace ( heap : List<T>, item : T) -> T: поменять местами кучу [1] и элемент _downheap( heap , начиная с индекса 1) return item
Поиск
Нахождение произвольного элемента занимает O(n) времени.
Удалить
Удаление произвольного элемента можно выполнить следующим образом:
- Найдите индекс элемента, который мы хотим удалить.
- Поменять этот элемент с последним элементом. Удалить последний элемент после обмена.
- Down-heapify или up-heapify для восстановления свойства кучи. В max-heap (min-heap) up-heapify требуется только тогда, когда новый ключ элемента больше (меньше) предыдущего, потому что может быть нарушено только свойство кучи родительского элемента. Предполагая, что свойство кучи было действительным между элементом и его дочерними элементами до обмена элементами, оно не может быть нарушено теперь большим (меньшим) значением ключа. Когда новый ключ меньше (больше) предыдущего, то требуется только down-heapify, потому что свойство кучи может быть нарушено только в дочерних элементах.
Уменьшить или увеличить клавишу
Операция уменьшения ключа заменяет значение узла с заданным значением на меньшее значение, а операция увеличения ключа делает то же самое, но с большим значением. Это включает в себя поиск узла с заданным значением, изменение значения, а затем down-heapifying или up-heapifying для восстановления свойства кучи.
Уменьшить клавишу можно следующим образом:
- Найдите индекс элемента, который мы хотим изменить.
- Уменьшить значение узла
- Down-heapify (предполагая максимальную кучу) для восстановления свойства кучи
Увеличить ключ можно следующим образом:
- Найдите индекс элемента, который мы хотим изменить.
- Увеличить ценность узла
- Up-heapify (предполагая максимальную кучу) для восстановления свойства кучи
Создание кучи
Построение кучи из массива из n входных элементов можно осуществить, начав с пустой кучи, а затем последовательно вставляя каждый элемент. Этот подход, называемый методом Уильямса в честь изобретателя двоичных куч, легко можно увидеть работающим за время O ( n log n ) : он выполняет n вставок по стоимости O (log n ) каждая. [a]
Однако метод Уильямса неоптимален. Более быстрый метод (благодаря Флойду [8] ) начинается с произвольного размещения элементов на бинарном дереве, учитывая свойство формы (дерево может быть представлено массивом, см. ниже). Затем, начиная с самого нижнего уровня и двигаясь вверх, просеиваем корень каждого поддерева вниз, как в алгоритме удаления, пока не будет восстановлено свойство кучи. Более конкретно, если все поддеревья, начинающиеся с некоторой высоты, уже были «кучированы» (самый нижний уровень соответствует ), деревья на высоте могут быть кучированы, отправив их корень вниз по пути максимально значимых потомков при построении максимальной кучи или минимально значимых потомков при построении минимальной кучи. Этот процесс занимает операций (обменов) на узел. В этом методе большая часть кучообразования происходит на нижних уровнях. Поскольку высота кучи равна , количество узлов на высоте равно . Следовательно, стоимость кучообразования всех поддеревьев равна:
При этом используется тот факт, что заданный бесконечный ряд сходится .
Известно, что точное значение вышеприведенного выражения (наихудшее число сравнений при построении кучи) равно:
- , [9] [б]
где s 2 ( n ) — сумма всех цифр двоичного представления числа n , а e 2 ( n ) — показатель степени числа 2 в разложении числа n на простые множители .
Средний случай сложнее для анализа, но можно показать, что он асимптотически приближается к 1,8814 n − 2 log 2 n + O (1) сравнений. [10] [11]
Следующая функция Build-Max-Heap преобразует массив A , который хранит полное двоичное дерево с n узлами, в max-heap, многократно используя Max-Heapify (down-heapify для max-heap) снизу вверх. Элементы массива, индексированные floor ( n /2) + 1 , floor ( n /2) + 2 , ..., n , являются листьями дерева (предполагая, что индексы начинаются с 1) — таким образом, каждый из них является кучей из одного элемента и не нуждается в down-heapify. Build-Max-Heap запускает Max-Heapify на каждом из оставшихся узлов дерева.
Build-Max-Heap ( A ): для каждого индекса i от пола ( длина ( A )/2) до 1 выполнить: Max-Heapify ( A , i )
Реализация кучи


Кучи обычно реализуются с помощью массива . Любое двоичное дерево может быть сохранено в массиве, но поскольку двоичная куча всегда является полным двоичным деревом, ее можно хранить компактно. Для указателей не требуется места ; вместо этого родительский и дочерний элементы каждого узла могут быть найдены с помощью арифметики по индексам массива. Эти свойства делают эту реализацию кучи простым примером неявной структуры данных или списка Ahnentafel . Детали зависят от положения корня, которое, в свою очередь, может зависеть от ограничений языка программирования, используемого для реализации, или предпочтений программиста. В частности, иногда корень помещается в индекс 1, чтобы упростить арифметику.
Пусть n будет числом элементов в куче, а i будет произвольным допустимым индексом массива, хранящего кучу. Если корень дерева находится в индексе 0, с допустимыми индексами от 0 до n − 1, то каждый элемент a в индексе i имеет
- дети с индексами 2 i + 1 и 2 i + 2
- его родительский элемент на индексном этаже (( i − 1) / 2).
В качестве альтернативы, если корень дерева находится в индексе 1 с допустимыми индексами от 1 до n , то каждый элемент a в индексе i имеет
- дети с индексами 2 i и 2 i +1
- его родительский элемент на индексном этаже ( i / 2).
Эта реализация используется в алгоритме пирамидальной сортировки , который повторно использует пространство, выделенное входному массиву, для хранения кучи (т.е. алгоритм выполняется на месте ). Эта реализация также полезна в качестве очереди с приоритетами . При использовании динамического массива возможна вставка неограниченного количества элементов.
Операции upheapor downheapмогут быть сформулированы в терминах массива следующим образом: предположим, что свойство кучи выполняется для индексов b , b +1, ..., e . Функция sift-down расширяет свойство кучи до b −1, b , b +1, ..., e . Только индекс i = b −1 может нарушить свойство кучи. Пусть j будет индексом наибольшего дочернего элемента a [ i ] (для max-heap или наименьшего дочернего элемента для min-heap) в диапазоне b , ..., e . (Если такого индекса не существует, потому что 2 i > e , то свойство кучи выполняется для нового расширенного диапазона, и ничего делать не нужно.) При перестановке значений a [ i ] и a [ j ] свойство кучи для позиции i устанавливается. На этом этапе единственная проблема заключается в том, что свойство кучи может не выполняться для индекса j . Функция sift-down применяется хвостовой рекурсией к индексу j до тех пор, пока свойство кучи не будет установлено для всех элементов.
Функция просеивания работает быстро. На каждом шаге ей нужно всего два сравнения и один обмен. Значение индекса, где она работает, удваивается на каждой итерации, так что требуется максимум log 2 e шагов.
Для больших куч и использования виртуальной памяти хранение элементов в массиве по вышеприведенной схеме неэффективно: (почти) каждый уровень находится на другой странице . B-кучи — это двоичные кучи, которые хранят поддеревья на одной странице, уменьшая количество страниц, к которым осуществляется доступ, вплоть до десятикратного. [12]
Операция слияния двух двоичных куч занимает Θ( n ) для куч одинакового размера. Лучшее, что вы можете сделать, это (в случае реализации массива) просто объединить два массива куч и построить кучу результата. [13] Кучу из n элементов можно объединить с кучей из k элементов, используя O(log n log k ) сравнений ключей, или, в случае реализации на основе указателей, за время O(log n log k ). [14] Алгоритм разделения кучи из n элементов на две кучи по k и nk элементов соответственно, основанный на новом представлении о кучах как упорядоченных коллекциях подкуч, был представлен в. [15] Алгоритм требует O(log n * log n ) сравнений. Представление также представляет новый и концептуально простой алгоритм слияния куч. Если слияние является распространенной задачей, рекомендуется использовать другую реализацию кучи, например, биномиальную кучи , которую можно объединить за O(log n ).
Кроме того, двоичная куча может быть реализована с помощью традиционной структуры данных двоичного дерева, но при добавлении элемента возникает проблема с поиском соседнего элемента на последнем уровне двоичной кучи. Этот элемент может быть определен алгоритмически или путем добавления дополнительных данных к узлам, что называется «разбиением» дерева — вместо того, чтобы просто хранить ссылки на потомков, мы также сохраняем инпорядоченного преемника узла.
Можно изменить структуру кучи, чтобы сделать возможным извлечение как наименьшего, так и наибольшего элемента за определенное время. [16] Для этого строки чередуются между минимальной кучей и максимальной кучей. Алгоритмы примерно одинаковы, но на каждом шаге необходимо учитывать чередующиеся строки с чередующимися сравнениями. Производительность примерно такая же, как у обычной однонаправленной кучи. Эту идею можно обобщить до минимально-максимально-медианной кучи.
Вывод индексных уравнений
В куче на основе массива дочерние и родительские элементы узла могут быть найдены с помощью простой арифметики по индексу узла. В этом разделе выводятся соответствующие уравнения для куч с корнем в индексе 0, с дополнительными примечаниями по кучам с корнем в индексе 1.
Чтобы избежать путаницы, мы определяем уровень узла как его расстояние от корня, так что сам корень занимает уровень 0.
Дочерние узлы
Для общего узла, расположенного по индексу i (начиная с 0), сначала выведем индекс его правого потомка, .
Пусть узел i находится на уровне L , и обратите внимание, что любой уровень l содержит ровно узлов. Более того, ровно узлов содержится в слоях до слоя l включительно (представьте себе двоичную арифметику; 0111...111 = 1000...000 - 1). Поскольку корень хранится в 0, узел k будет храниться в индексе . Объединение этих наблюдений дает следующее выражение для индекса последнего узла в слое l .
Пусть после узла i в слое L имеется j узлов , таких что
Каждый из этих j узлов должен иметь ровно 2 дочерних узла, поэтому должны быть узлы, отделяющие правого дочернего узла i от конца его слоя ( ).
Заметив, что левый дочерний элемент любого узла всегда находится на 1 позицию раньше своего правого дочернего элемента, получаем .
Если корень расположен в индексе 1 вместо 0, последний узел на каждом уровне находится в индексе . Использование этого повсюду приводит к и для куч с корнем в 1.
Родительский узел
Каждый некорневой узел является либо левым, либо правым дочерним элементом своего родителя, поэтому должно выполняться одно из следующих условий:
Следовательно,
Теперь рассмотрим выражение .
Если узел является левым потомком, это дает результат немедленно, однако, это также дает правильный результат, если узел является правым потомком. В этом случае должно быть четным, и, следовательно, должно быть нечетным.
Поэтому, независимо от того, является ли узел левым или правым потомком, его родителя можно найти с помощью выражения:
Связанные структуры
Поскольку порядок родственных элементов в куче не определяется свойством кучи, два дочерних элемента одного узла могут свободно меняться местами, если только это не нарушает свойство формы (сравните с treap ). Обратите внимание, однако, что в общей куче на основе массива простая замена дочерних элементов может также потребовать перемещения узлов поддерева дочерних элементов для сохранения свойства кучи.
Двоичная куча является частным случаем d-арной кучи, в которой d = 2.
Сводка времени работы
Вот временные сложности [17] различных структур данных кучи. Сокращение am. указывает на то, что данная сложность амортизирована, в противном случае это сложность наихудшего случая. Для значения " O ( f )" и " Θ ( f )" см . нотацию Big O. Имена операций предполагают минимальную кучу.
| Операция | найти-мин | удалить-мин | клавиша уменьшения | вставлять | сливаться | сделать-кучу [c] |
|---|---|---|---|---|---|---|
| Двоичный [17] | Θ (1) | Θ (лог n ) | Θ (лог n ) | Θ (лог n ) | Θ ( н ) | Θ ( н ) |
| Наклон [18] | Θ (1) | О (лог н ) утра. | О (лог н ) утра. | О (лог н ) утра. | О (лог н ) утра. | Θ ( н ) ам. |
| Левый [19] | Θ (1) | Θ (лог n ) | Θ (лог n ) | Θ (лог n ) | Θ (лог n ) | Θ ( н ) |
| Биномиальное [17] [21] | Θ (1) | Θ (лог n ) | Θ (лог n ) | Θ (1) утра. | Θ (log n ) [d] | Θ ( н ) |
| Косой бином [22] | Θ (1) | Θ (лог n ) | Θ (лог n ) | Θ (1) | Θ (log n ) [d] | Θ ( н ) |
| 2–3 куча [24] | Θ (1) | О (лог н ) утра. | Θ (1) | Θ (1) утра. | О (log n ) [d] | Θ ( н ) |
| Перекос снизу вверх [18] | Θ (1) | О (лог н ) утра. | О (лог н ) утра. | Θ (1) утра. | Θ (1) утра. | Θ ( н ) ам. |
| Сопряжение [25] | Θ (1) | О (лог н ) утра. | о (лог н ) ам. [э] | Θ (1) | Θ (1) | Θ ( н ) |
| Ранг-пары [28] | Θ (1) | О (лог н ) утра. | Θ (1) утра. | Θ (1) | Θ (1) | Θ ( н ) |
| Фибоначчи [17] [29] | Θ (1) | О (лог н ) утра. | Θ (1) утра. | Θ (1) | Θ (1) | Θ ( н ) |
| Строгий Фибоначчи [30] [ф] | Θ (1) | Θ (лог n ) | Θ (1) | Θ (1) | Θ (1) | Θ ( н ) |
| Бродал [31] [ж] | Θ (1) | Θ (лог n ) | Θ (1) | Θ (1) | Θ (1) | Θ ( н ) [32] |
- ^ Фактически, можно показать, что эта процедура занимает Θ( n log n ) времени в худшем случае , а это означает, что n log n также является асимптотической нижней границей сложности. [1] : 167 Однако в среднем случае (усреднение по всем перестановкам n входов) метод занимает линейное время. [8]
- ^ Это не означает, что сортировку можно выполнить за линейное время, поскольку построение кучи — это только первый шаг алгоритма пирамидальной сортировки .
- ^ make-heap — это операция построения кучи из последовательности из n неотсортированных элементов. Она может быть выполнена за время Θ ( n ), когда meld выполняется за время O (log n ) (где обе сложности могут быть амортизированы). [18] [19] Другой алгоритм достигает Θ ( n ) для двоичных куч. [20]
- ^ abc Для постоянных куч (не поддерживающих reduce-key ) общее преобразование снижает стоимость meld до стоимости insert , в то время как новая стоимость delete-min является суммой старых стоимостей delete-min и meld . [23] Здесь это заставляет meld работать за Θ (1) время (амортизированное, если стоимость insert равна ), в то время как delete-min по-прежнему работает за O (log n ). Применительно к перекошенным биномиальным кучам это дает очереди Бродала-Окасаки, постоянные кучи с оптимальной сложностью в худшем случае. [22]
- ^ Нижняя граница [26] верхняя граница [27]
- ^ ab Очереди Бродала и строгие кучи Фибоначчи достигают оптимальных сложностей в худшем случае для куч. Они были впервые описаны как императивные структуры данных. Очередь Бродала-Окасаки — это постоянная структура данных, достигающая того же оптимума, за исключением того, что ключ уменьшения не поддерживается.
Ссылки
- ^ аб Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03384-4.
- ^ Уильямс, JWJ (1964), «Алгоритм 232 — Пирамидальная сортировка», Сообщения ACM , 7 (6): 347– 348, doi :10.1145/512274.512284
- ^ Y Narahari, «Двоичные кучи», Структуры данных и алгоритмы
- ^ Портер, Томас; Саймон, Иштван (сентябрь 1975 г.). «Случайная вставка в структуру очереди с приоритетами». IEEE Transactions on Software Engineering . SE-1 (3): 292– 298. doi :10.1109/TSE.1975.6312854. ISSN 1939-3520. S2CID 18907513.
- ^ Mehlhorn, Kurt; Tsakalidis, A. (февраль 1989). "Data structures". Universität des Saarlandes : 27. doi :10.22028/D291-26123.
Porter и Simon [171] проанализировали среднюю стоимость вставки случайного элемента в случайную кучу с точки зрения обменов. Они доказали, что это среднее значение ограничено константой 1,61. Их доказательство не обобщается на последовательности вставок, поскольку случайные вставки в случайные кучи не создают случайные кучи. Проблема повторной вставки была решена Bollobas и Simon [27]; они показывают, что ожидаемое число обменов ограничено 1,7645. Худшая стоимость вставок и удалений была изучена Gonnet и Munro [84]; они дают границы log log n + O(1) и log n + log n* + O(1) для числа сравнений соответственно.
- ^ "python/cpython/heapq.py". GitHub . Получено 2020-08-07 .
- ^ "heapq — Алгоритм очереди кучи — Документация Python 3.8.5". docs.python.org . Получено 2020-08-07 .
heapq.heappushpop(heap, item): Поместить элемент в кучу, затем извлечь и вернуть наименьший элемент из кучи. Объединенное действие выполняется эффективнее, чем heappush() с последующим отдельным вызовом heappop().
- ^ ab Hayward, Ryan; McDiarmid, Colin (1991). "Average Case Analysis of Heap Building by Repeated Insertion" (PDF) . J. Algorithms . 12 : 126– 153. CiteSeerX 10.1.1.353.7888 . doi :10.1016/0196-6774(91)90027-v. Архивировано из оригинала (PDF) 2016-02-05 . Получено 2016-01-28 .
- ^ Suchenek, Marek A. (2012), «Элементарный, но точный анализ худшего случая программы построения кучи Флойда», Fundamenta Informaticae , 120 (1): 75–92 , doi :10.3233/FI-2012-751.
- ^ Доберкат, Эрнст Э. (май 1984). "Анализ среднего случая алгоритма Флойда для построения куч" (PDF) . Информация и управление . 6 (2): 114– 131. doi : 10.1016/S0019-9958(84)80053-4 .
- ^ Пасанен, Томи (ноябрь 1996 г.). Элементарный анализ среднего случая алгоритма Флойда для построения куч (технический отчет). Центр компьютерных наук Турку. CiteSeerX 10.1.1.15.9526 . ISBN 951-650-888-XТехнический отчет TUCS № 64. Обратите внимание, что в этой статье используется оригинальный термин Флойда «просеивание вверх» для того, что сейчас называется просеиванием вниз .
- ↑ Камп, Поул-Хеннинг (11 июня 2010 г.). «Вы делаете это неправильно». ACM Queue . Том 8, № 6.
- ^ Крис Л. Кушмаул. "двоичная куча" Архивировано 08.08.2008 на Wayback Machine . Словарь алгоритмов и структур данных, под ред. Пола Э. Блэка, Национальный институт стандартов и технологий США. 16 ноября 2009 г.
- ^ Дж.-Р. Сак и Т. Штротхотте «Алгоритм слияния куч», Acta Informatica 22, 171-186 (1985).
- ^ Сак, Йорг-Рюдигер; Штротхотте, Томас (1990). «Характеристика куч и ее применение». Информация и вычисления . 86 : 69– 86. doi : 10.1016/0890-5401(90)90026-E .
- ^ Аткинсон, MD; Дж.-Р. Сак ; Н. Санторо и Т. Стротхотте (1 октября 1986 г.). "Min-max heaps and generalized priority queues" (PDF) . Методы программирования и структуры данных. Comm. ACM, 29(10): 996–1000. Архивировано из оригинала (PDF) 27 января 2007 г. Получено 29 апреля 2008 г.
- ^ abcd Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л. (1990). Введение в алгоритмы (1-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03141-8.
- ^ abc Sleator, Daniel Dominic ; Tarjan, Robert Endre (февраль 1986 г.). «Саморегулирующиеся кучи». SIAM Journal on Computing . 15 (1): 52– 69. CiteSeerX 10.1.1.93.6678 . doi :10.1137/0215004. ISSN 0097-5397.
- ^ ab Tarjan, Robert (1983). "3.3. Левые кучи". Структуры данных и сетевые алгоритмы . С. 38–42 . doi :10.1137/1.9781611970265. ISBN 978-0-89871-187-5.
- ^ Хейворд, Райан; МакДиармид, Колин (1991). "Анализ среднего случая построения кучи путем повторной вставки" (PDF) . J. Algorithms . 12 : 126– 153. CiteSeerX 10.1.1.353.7888 . doi :10.1016/0196-6774(91)90027-v. Архивировано из оригинала (PDF) 2016-02-05 . Получено 2016-01-28 .
- ^ "Биномиальная куча | Brilliant Math & Science Wiki". brilliant.org . Получено 2019-09-30 .
- ^ ab Brodal, Gerth Stølting; Okasaki, Chris (ноябрь 1996 г.), «Оптимальные чисто функциональные очереди с приоритетами», Journal of Functional Programming , 6 (6): 839–857 , doi : 10.1017/s095679680000201x
- ^ Окасаки, Крис (1998). "10.2. Структурная абстракция". Чисто функциональные структуры данных (1-е изд.). С. 158–162 . ISBN 9780521631242.
- ^ Такаока, Тадао (1999), Теория 2–3 куч (PDF) , стр. 12
- ^ Яконо, Джон (2000), «Улучшенные верхние границы для парных куч», Труды 7-го Скандинавского семинара по теории алгоритмов (PDF) , Lecture Notes in Computer Science, т. 1851, Springer-Verlag, стр. 63–77 , arXiv : 1110.4428 , CiteSeerX 10.1.1.748.7812 , doi : 10.1007/3-540-44985-X_5, ISBN 3-540-67690-2
- ^ Фредман, Майкл Лоуренс (июль 1999 г.). «Об эффективности парных куч и связанных с ними структур данных» (PDF) . Журнал Ассоциации вычислительной техники . 46 (4): 473– 501. doi :10.1145/320211.320214.
- ^ Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF) . Труды FOCS '05 46-го ежегодного симпозиума IEEE по основам компьютерной науки. стр. 174–183 . CiteSeerX 10.1.1.549.471 . doi :10.1109/SFCS.2005.75. ISBN 0-7695-2468-0.
- ^ Хёплер, Бернхард; Сен, Сиддхартха; Тарьян, Роберт Э. (ноябрь 2011 г.). «Кучи ранговых пар» (PDF) . СИАМ Дж. Компьютерные технологии . 40 (6): 1463–1485 . doi : 10.1137/100785351.
- ^ Фредман, Майкл Лоуренс ; Тарьян, Роберт Э. (июль 1987 г.). «Кучи Фибоначчи и их использование в улучшенных алгоритмах сетевой оптимизации» (PDF) . Журнал Ассоциации вычислительной техники . 34 (3): 596– 615. CiteSeerX 10.1.1.309.8927 . doi :10.1145/28869.28874.
- ^ Бродал, Герт Столтинг ; Лагогианнис, Джордж; Тарьян, Роберт Э. (2012). Строгие кучи Фибоначчи (PDF) . Труды 44-го симпозиума по теории вычислений - STOC '12. стр. 1177–1184 . CiteSeerX 10.1.1.233.1740 . doi :10.1145/2213977.2214082. ISBN 978-1-4503-1245-5.
- ^ Бродал, Герт С. (1996), «Эффективные очереди с приоритетами в наихудшем случае» (PDF) , Труды 7-го ежегодного симпозиума ACM-SIAM по дискретным алгоритмам , стр. 52–58
- ^ Гудрич, Майкл Т .; Тамассиа, Роберто (2004). "7.3.6. Построение кучи снизу вверх". Структуры данных и алгоритмы в Java (3-е изд.). С. 338–341 . ISBN 0-471-46983-1.
Внешние ссылки
- Открытые структуры данных - Раздел 10.1 - BinaryHeap: неявное двоичное дерево, Пэт Морин
- Реализация двоичной максимальной кучи на языке C Робина Томаса
- Реализация двоичной минимальной кучи на языке C Робином Томасом