Соленоидальное векторное поле

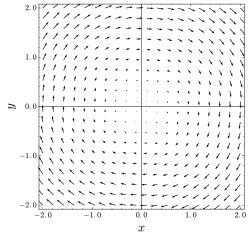
В векторном исчислении соленоидальное векторное поле (также известное как несжимаемое векторное поле , бездивергентное векторное поле или поперечное векторное поле ) — это векторное поле v с нулевой дивергенцией во всех точках поля: Обычный способ выражения этого свойства — сказать, что поле не имеет источников или стоков. ^{[примечание 1]} $${\displaystyle \nabla \cdot \mathbf {v} =0.}$$

Теорема о дивергенции дает эквивалентное интегральное определение соленоидального поля, а именно, что для любой замкнутой поверхности суммарный поток через поверхность должен быть равен нулю:

${\displaystyle \;\;\mathbf {v} \cdot \,d\mathbf {S} =0,}$

где — внешняя нормаль к каждому элементу поверхности.${\displaystyle d\mathbf {S} }$

Основная теорема векторного исчисления гласит, что любое векторное поле может быть выражено как сумма безвихревого и соленоидального полей. Условие нулевой дивергенции выполняется всякий раз, когда векторное поле v имеет только компоненту векторного потенциала , поскольку определение векторного потенциала A как: автоматически приводит к тождеству (как можно показать, например, с помощью декартовых координат): Обратное также верно: для любого соленоидального v существует векторный потенциал A такой, что (Строго говоря, это выполняется при определенных технических условиях на v , см. разложение Гельмгольца .)$${\displaystyle \mathbf {v} =\nabla \times \mathbf {A} }$$$${\displaystyle \nabla \cdot \mathbf {v} =\nabla \cdot (\nabla \times \mathbf {A}) = 0.}$$${\displaystyle \mathbf {v} =\nabla \times \mathbf {A}.}$

Слово «соленоидальный» происходит от греческого слова σωληνοειδές (sōlēnoeidēs), что означает «трубчатый», от σωλην (sōlēn) или труба.

• Магнитное поле B (см. закон Гаусса для магнетизма )
• Поле скоростей потока несжимаемой жидкости
• Поле вихреобразования​
• Электрическое поле E в нейтральных областях ( );${\displaystyle \rho _{e}=0}$
• Плотность тока J при неизменной плотности заряда .${\textstyle {\frac {\partial \rho _{e}}{\partial t}}=0}$
• Магнитный векторный потенциал А в кулоновской калибровке

• Продольные и поперечные векторные поля
• Функция потока
• Консервативное векторное поле

• Арис, Резерфорд (1989), Векторы, тензоры и основные уравнения механики жидкости, Довер, ISBN 0-486-66110-5