Максимальная равномерность

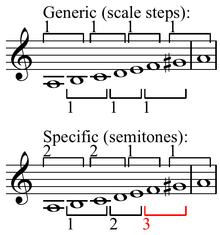
В теории гамм (музыки) максимально четный набор (гамма) — это тот, в котором каждый общий интервал имеет либо один, либо два последовательных целых числа конкретных интервала — другими словами, гамма, ноты (ПК) которой «разнесены максимально». Это свойство впервые описали Джон Клаф и Джек Даутетт. [1] Клаф и Даутетт также ввели максимально четный алгоритм. Для хроматической мощности c и мощности ПК-множества d максимально четный набор — это
где k изменяется от 0 до d − 1 и m , 0 ≤ m ≤ c − 1 фиксировано, а пара скобок является функцией пола . Обсуждение этих концепций можно найти в книге Тимоти Джонсона о математических основах теории диатонической шкалы. [2] Джек Даутетт и Ричард Кранц ввели максимально четные множества в математическую литературу. [3] [4]
Говорят, что гамма имеет свойство Майхилла, если каждый общий интервал представлен двумя определенными размерами интервала , а гамма со свойством Майхилла называется хорошо сформированной гаммой . [5] Диатоническая коллекция является как хорошо сформированной гаммой, так и максимально ровной. Целотонная гамма также максимально ровной, но она не является хорошо сформированной, поскольку каждый общий интервал представлен только одним размером.
Максимальная ровность второго порядка — это максимальная ровность подколлекции большего набора, который является максимально ровным. Диатонические трезвучия и септаккорды обладают максимальной ровностью второго порядка, будучи максимально ровными относительно максимально ровных диатонических гамм, но не максимально ровными относительно хроматических гамм. (там же, стр. 115) Это вложенное качество напоминает «редукционный формат» Фреда Лердаля [ 6] для пространства высоты тона снизу вверх:
| С | Э | Г | С | |||||||||
| С | Д | Э | Ф | Г | А | Б | С | |||||
| С | Д♭ | Д | Э♭ | Э | Ф | Ф♯ | Г | А♭ | А | B♭ | Б | С |
- (Лердаль, 1992)
В динамическом подходе были построены вращающиеся концентрические окружности и итерированные максимально четные множества. Этот подход имеет значение в неоримановой теории и приводит к некоторым интересным связям между диатонической и хроматической теорией. [7] Эммануэль Амио открыл еще один способ определения максимально четных множеств с использованием дискретных преобразований Фурье . [8] [9]
Кэри, Норман и Клэмпитт, Дэвид (1989). «Аспекты хорошо сформированных гамм», Music Theory Spectrum 11: 187–206.
Ссылки
- ^ Клаф, Джон; Дутетт, Джек (1991). «Максимально четные наборы». Журнал теории музыки . 35 (35): 93– 173. doi :10.2307/843811. JSTOR 843811.
- ^ Джонсон, Тимоти (2003). Основы диатонической теории: математический подход к музыкальным основам . Key College Publishing. ISBN 1-930190-80-8.
- ^ Дутетт, Джек; Кранц, Ричард (2007). «Максимально четные множества и конфигурации: общие темы в математике, физике и музыке». Журнал комбинаторной оптимизации . 14 (4): 385-410. doi :10.1007/s10878-006-9041-5. S2CID 41964397.
- ^ Дутетт, Джек; Кранц, Ричард (2007). «Обеденные столы и концентрические круги: гармония математики, музыки и физики». College Mathematics Journal . 39 (3): 203-211. doi :10.1080/07468342.2008.11922294. S2CID 117686406.
- ^ Кэри, Норман; Клампитт, Дэвид (1989). «Аспекты хорошо сформированных гамм». Music Theory Spectrum . 11 (2): 187– 206. doi :10.2307/745935. JSTOR 745935.
- ^ Лердаль, Фред (1992). «Когнитивные ограничения в композиционных системах». Contemporary Music Review . 6 (2): 97-121. CiteSeerX 10.1.1.168.1343 . doi :10.1080/07494469200640161.
- ^ Douthett, Jack (2008). "Filter Point-Symmetry and Dynamical Voice-Leading". Музыка и математика: аккорды, коллекции и преобразования . Eastman Studies in Music: 72-106. Ред. J. Douthett, M. Hyde и C. Smith. University of Rochester Press, NY. doi : 10.1017/9781580467476.006. ISBN 9781580467476. ISBN 1-58046-266-9 .
- ^ Армиот, Эммануэль (2007). «Дэвид Левин и максимально четные множества». Журнал математики и музыки . 1 (3): 157-172. doi :10.1080/17459730701654990. S2CID 120481485.
- ^ Армиот, Эммануэль (2016). Музыка через пространство Фурье: Дискретное преобразование Фурье в теории музыки . Springer. ISBN 9783319455808.
