Формализмы вращения в трех измерениях
В геометрии существуют различные формализмы для выражения вращения в трех измерениях как математического преобразования . В физике эта концепция применяется к классической механике , где вращательная (или угловая) кинематика является наукой количественного описания чисто вращательного движения . Ориентация объекта в данный момент времени описывается теми же инструментами, поскольку она определяется как воображаемое вращение из исходного положения в пространстве, а не фактически наблюдаемое вращение из предыдущего положения в пространстве.
Согласно теореме Эйлера о вращении , вращение твердого тела (или трехмерной системы координат с фиксированным началом ) описывается одним вращением вокруг некоторой оси. Такое вращение может быть однозначно описано минимум тремя действительными параметрами. Однако по разным причинам существует несколько способов его представления. Многие из этих представлений используют больше необходимого минимума в три параметра, хотя каждый из них по-прежнему имеет только три степени свободы .
Примером использования представления вращения является компьютерное зрение , где автоматизированному наблюдателю необходимо отслеживать цель. Рассмотрим твердое тело с тремя ортогональными единичными векторами, закрепленными на его теле (представляющими три оси локальной системы координат объекта ). Основная проблема заключается в указании ориентации этих трех единичных векторов , а следовательно, и твердого тела, относительно системы координат наблюдателя, рассматриваемой как опорное размещение в пространстве.
Вращения и движения
Формализмы вращения сосредоточены на собственных ( сохраняющих ориентацию ) движениях евклидова пространства с одной неподвижной точкой , к которой относится вращение . Хотя физические движения с неподвижной точкой являются важным случаем (например, описанные в системе центра масс или движения сустава ) , этот подход создает знание обо всех движениях. Любое собственное движение евклидова пространства разлагается на вращение вокруг начала координат и перенос . Каким бы ни был порядок их композиции , «чистая» компонента вращения не изменится, однозначно определяемая полным движением.
Можно также понимать «чистые» вращения как линейные отображения в векторном пространстве, снабженном евклидовой структурой, а не как отображения точек соответствующего аффинного пространства . Другими словами, формализм вращения охватывает только вращательную часть движения, которая содержит три степени свободы, и игнорирует трансляционную часть, которая содержит еще три.
При представлении вращения в виде чисел на компьютере некоторые люди предпочитают представление кватерниона или представление оси+угла, поскольку они позволяют избежать карданного захвата , который может возникнуть при вращениях Эйлера. [1]
Альтернативы формализма
Матрица вращения
Вышеупомянутая триада единичных векторов также называется базисом . Указание координат ( компонент ) векторов этого базиса в его текущем (повернутом) положении в терминах опорных (неповернутых) осей координат полностью опишет поворот. Три единичных вектора, û , v̂ и ŵ , которые образуют повернутый базис, состоят каждый из 3 координат, что дает в общей сложности 9 параметров.
Эти параметры можно записать как элементы матрицы A размером 3 × 3 , называемой матрицей вращения . Обычно координаты каждого из этих векторов располагаются вдоль столбца матрицы (однако следует помнить, что существует и широко используется альтернативное определение матрицы вращения, в котором координаты векторов, определенные выше, располагаются по строкам [2] ).
Не все элементы матрицы вращения независимы — как гласит теорема Эйлера о вращении, матрица вращения имеет только три степени свободы.
Матрица вращения имеет следующие свойства:
- A — действительная ортогональная матрица , поэтому каждая ее строка или столбец представляет собой единичный вектор .
- Собственные значения матрицы A равны , где i — стандартная мнимая единица со свойством i 2 = −1
- Определитель матрицы А равен +1, что эквивалентно произведению ее собственных значений .
- След A равен 1 + 2 cos θ , что эквивалентно сумме его собственных значений.
Угол θ , который появляется в выражении собственного значения, соответствует углу оси Эйлера и представлению угла. Собственный вектор, соответствующий собственному значению 1, является сопутствующей осью Эйлера, поскольку ось является единственным (ненулевым) вектором, который остается неизменным при умножении слева (повороте) на матрицу поворота.
Вышеуказанные свойства эквивалентны , что является другим способом утверждения, что ( û , v̂ , ŵ ) образуют 3D ортонормированный базис . Эти утверждения включают в общей сложности 6 условий (в перекрестном произведении их 3), оставляя матрицу вращения всего с 3 степенями свободы, как и требуется.
Два последовательных поворота, представленных матрицами A 1 и A 2, легко объединяются как элементы группы (обратите внимание на порядок, поскольку вектор, который поворачивается, умножается справа).
Легкость, с которой векторы можно вращать с помощью матрицы вращения, а также простота объединения последовательных вращений делают матрицу вращения полезным и популярным способом представления вращений, хотя она и менее лаконична, чем другие представления.
Ось Эйлера и угол (вектор вращения)

Из теоремы Эйлера о вращении мы знаем, что любое вращение можно выразить как одиночное вращение вокруг некоторой оси. Ось — это единичный вектор (уникальный, за исключением знака), который остается неизменным при вращении. Величина угла также уникальна, а ее знак определяется знаком оси вращения.
Ось можно представить как трехмерный единичный вектор , а угол — как скаляр θ .
Поскольку ось нормализована, она имеет только две степени свободы . Угол добавляет третью степень свободы к этому представлению вращения.
Можно выразить вращение как вектор вращения , или вектор Эйлера , ненормализованный трехмерный вектор, направление которого определяет ось, а длина которого равна θ ,
Вектор вращения полезен в некоторых контекстах, поскольку он представляет трехмерное вращение только с тремя скалярными значениями (его компонентами), представляющими три степени свободы. Это также верно для представлений, основанных на последовательностях трех углов Эйлера (см. ниже).
Если угол поворота θ равен нулю, ось не определена однозначно. Объединение двух последовательных поворотов, каждый из которых представлен осью Эйлера и углом, не является простым и фактически не удовлетворяет закону сложения векторов, который показывает, что конечные повороты на самом деле не являются векторами. Лучше всего использовать матрицу поворота или кватернионную нотацию, вычислить произведение, а затем преобразовать обратно в ось Эйлера и угол.
Повороты Эйлера
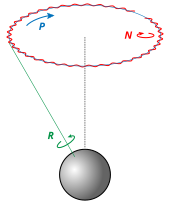
Идея вращений Эйлера заключается в том, чтобы разделить полное вращение системы координат на три более простых конститутивных вращения, называемых прецессией , нутацией и внутренним вращением , каждое из которых является приращением одного из углов Эйлера . Обратите внимание, что внешняя матрица будет представлять вращение вокруг одной из осей системы отсчета, а внутренняя матрица представляет вращение вокруг одной из осей подвижной системы отсчета. Средняя матрица представляет вращение вокруг промежуточной оси, называемой линией узлов .
Однако определение углов Эйлера не является единственным, и в литературе используется много различных соглашений. Эти соглашения зависят от осей, вокруг которых выполняются вращения, и их последовательности (поскольку вращения на сфере некоммутативны ) .
Используемое соглашение обычно указывается путем указания осей, вокруг которых происходят последовательные вращения (до их составления), ссылаясь на них индексом (1, 2, 3) или буквой (X, Y, Z) . Инженерные и робототехнические сообщества обычно используют углы Эйлера 3-1-3. Обратите внимание, что после составления независимых вращений они больше не вращаются вокруг своей оси. Самая внешняя матрица вращает другие две, оставляя вторую матрицу вращения над линией узлов, а третью — в кадре, движущемся вместе с телом. Существует 3 × 3 × 3 = 27 возможных комбинаций трех основных вращений, но только 3 × 2 × 2 = 12 из них можно использовать для представления произвольных трехмерных вращений в виде углов Эйлера. Эти 12 комбинаций избегают последовательных вращений вокруг одной и той же оси (например, XXY), что уменьшило бы степени свободы, которые могут быть представлены.
Поэтому углы Эйлера никогда не выражаются в терминах внешней системы отсчета или в терминах сопутствующей вращающейся системы отсчета тела, а в смеси. Другие соглашения (например, матрица вращения или кватернионы ) используются для того, чтобы избежать этой проблемы.
В авиации ориентация самолета обычно выражается в виде внутренних углов Тейта-Брайена , следующих за соглашением z - y ′- x ″ , которые называются курсом , углом места и креном (или синонимами рысканием , тангажом и креном ).
Кватернионы
Кватернионы , которые образуют четырехмерное векторное пространство , оказались очень полезными для представления вращений благодаря ряду преимуществ по сравнению с другими представлениями, упомянутыми в этой статье.
Кватернионное представление вращения записывается в виде версора (нормализованного кватерниона):
Приведенное выше определение сохраняет кватернион как массив, следуя соглашению, используемому в (Wertz 1980) и (Markley 2003). Альтернативное определение, используемое, например, в (Coutsias 1999) и (Schmidt 2001), определяет «скалярный» член как первый элемент кватерниона, а остальные элементы смещены на одну позицию вниз.
В терминах оси Эйлера
и угол θ компоненты этого версора выражаются следующим образом:
Проверка показывает, что параметризация кватерниона подчиняется следующему ограничению:
Последний член (в нашем определении) часто называют скалярным членом, который берет свое начало в кватернионах, если понимать их как математическое расширение комплексных чисел, записанных как и где { i , j , k } — гиперкомплексные числа, удовлетворяющие
Умножение кватернионов, которое используется для задания составного вращения, выполняется таким же образом, как умножение комплексных чисел , за исключением того, что порядок элементов должен быть принят во внимание, поскольку умножение не является коммутативным. В матричной нотации мы можем записать умножение кватернионов как
Объединение двух последовательных кватернионных вращений, таким образом, так же просто, как использование матрицы вращения. Так же, как объединяются две последовательные матрицы вращения, A 1 , за которыми следует A 2 , мы можем представить это с помощью параметров кватерниона аналогичным лаконичным способом:
Кватернионы являются очень популярной параметризацией благодаря следующим свойствам:
- Более компактно, чем матричное представление, и менее подвержено ошибкам округления.
- Элементы кватерниона непрерывно изменяются по единичной сфере в ℝ 4 (обозначается как S 3 ) по мере изменения ориентации, избегая прерывистых скачков (присущих трехмерным параметризациям)
- Выражение матрицы вращения через параметры кватерниона не содержит тригонометрических функций.
- Легко объединить два отдельных вращения, представленных в виде кватернионов, используя кватернионное произведение.
Как и матрицы вращения, кватернионы иногда должны быть перенормированы из-за ошибок округления, чтобы убедиться, что они соответствуют допустимым вращениям. Однако вычислительные затраты на перенормировку кватерниона намного меньше, чем на нормализацию матрицы 3 × 3 .
Кватернионы также отражают спинорный характер вращений в трех измерениях. Для трехмерного объекта, связанного с его (фиксированным) окружением слабыми струнами или полосами, струны или полосы могут быть распутаны после двух полных оборотов вокруг некоторой фиксированной оси из начального распутанного состояния. Алгебраически кватернион, описывающий такое вращение, изменяется от скаляра +1 (изначально), через (скаляр + псевдовектор) значения до скаляра −1 (за один полный оборот), через (скаляр + псевдовектор) значения обратно до скаляра +1 (за два полных оборота). Этот цикл повторяется каждые 2 оборота. После 2 n оборотов (целое число n > 0 ), без каких-либо промежуточных попыток распутывания, струны/полосы могут быть частично распутаны обратно в состояние 2( n − 1) оборотов с каждым применением той же процедуры, которая использовалась при распутывании от 2 оборотов до 0 оборотов. Применение той же процедуры n раз вернет 2 n -запутанный объект обратно в распутанное или 0-оборотное состояние. Процесс распутывания также удаляет любое скручивание, вызванное вращением вокруг самих струн/лент. Для демонстрации этих фактов можно использовать простые 3D-механические модели.
Вектор Родригеса
Вектор Родригеса (иногда называемый вектором Гиббса , с координатами, называемыми параметрами Родригеса ) [3] [4] можно выразить через ось и угол поворота следующим образом:
Это представление является многомерным аналогом гномонической проекции , отображающей единичные кватернионы из 3-мерной сферы на 3-мерную чисто векторную гиперплоскость.
Он имеет разрыв при 180° ( π радиан): поскольку любой вектор вращения r стремится к углу π радиан, его тангенс стремится к бесконечности.
Вращение g, за которым следует вращение f в представлении Родригеса, имеет простую форму композиции вращений
Сегодня наиболее простым способом доказательства этой формулы является ее (точное) дублетное представление , где g = n̂ tan a и т. д.
Комбинаторные особенности вывода матрицы Паули, упомянутые выше, также идентичны эквивалентному выводу кватерниона ниже. Постройте кватернион, связанный с пространственным вращением R , как, Тогда композиция вращения R B с R A представляет собой вращение R C = R B R A , с осью вращения и углом, определяемыми произведением кватернионов, то есть
Разверните это кватернионное произведение до
Разделите обе части этого уравнения на тождество, полученное из предыдущего, и оцените
Это формула Родригеса для оси составного вращения, определяемой через оси двух компонентных вращений. Он вывел эту формулу в 1840 году (см. стр. 408). [3] Три оси вращения A , B и C образуют сферический треугольник, а двугранные углы между плоскостями, образованными сторонами этого треугольника, определяются углами вращения.
Модифицированные параметры Родригеса (MRP) могут быть выражены через ось Эйлера и угол: Его компоненты могут быть выражены через компоненты единичного кватерниона, представляющего то же вращение, что и
Модифицированный вектор Родригеса — это стереографическая проекция, отображающая единичные кватернионы из 3-сферы на 3-мерную чисто векторную гиперплоскость. Проекция противоположного кватерниона − q приводит к другому модифицированному вектору Родригеса p s , чем проекция исходного кватерниона q . Сравнивая компоненты, получаем, что Примечательно, что если один из этих векторов лежит внутри единичной 3-сферы, другой будет лежать снаружи.
Параметры Кэли–Клейна
См. определение на сайте Wolfram Mathworld.
Аналоги более высоких измерений
Закон преобразования вектора
Активные вращения трехмерного вектора p в евклидовом пространстве вокруг оси n на угол η можно легко записать в терминах скалярных и векторных произведений следующим образом:
где — продольная составляющая p вдоль n , заданная скалярным произведением , — поперечная составляющая p относительно n , и
является перекрестным произведением p и n .
Вышеприведенная формула показывает, что продольный компонент p остается неизменным, тогда как поперечная часть p вращается в плоскости, перпендикулярной n . Эта плоскость охватывается самой поперечной частью p и направлением, перпендикулярным как p , так и n . Вращение непосредственно идентифицируется в уравнении как двумерное вращение на угол η .
Пассивные вращения можно описать той же формулой, но с обратным знаком η или n .
Формулы преобразования между формализмами
Матрица вращения ↔ Углы Эйлера
Углы Эйлера ( φ , θ , ψ ) можно извлечь из матрицы вращения A, проверив матрицу вращения в аналитической форме.
Матрица вращения → Углы Эйлера (з - х - звнешний)
Используя x -соглашение, 3-1-3 внешних угла Эйлера φ , θ и ψ (вокруг оси z , оси x и снова оси θ) можно получить следующим образом:
Обратите внимание, что atan2( a , b ) эквивалентно arctan а/б где также учитывается квадрант , в котором находитсяточка ( b , a ) ; см. atan2 .
При осуществлении преобразования необходимо учитывать несколько ситуаций: [5]
- Обычно существует два решения в интервале [− π , π ] 3. Приведенная выше формула работает только тогда, когда θ находится в интервале [0, π ] .
- Для особого случая A 33 = 0 , φ и ψ будут получены из A 11 и A 12 .
- Существует бесконечно много, но счетно много решений вне интервала [− π , π ] 3 .
- Применимость всех математических решений для конкретного приложения зависит от ситуации.
Углы Эйлера (z - y ′- x ″внутренняя) → матрица вращения
Матрица вращения A генерируется из внутренних углов Эйлера 3-2-1 путем умножения трех матриц, генерируемых вращениями вокруг осей.
Оси вращения зависят от конкретной используемой конвенции. Для конвенции x вращения происходят вокруг осей x , y и z с углами ϕ , θ и ψ , отдельные матрицы следующие:
Это дает Примечание: Это справедливо для правосторонней системы, которая является соглашением, используемым почти во всех инженерных и физических дисциплинах.
Интерпретация этих правосторонних матриц вращения заключается в том, что они выражают преобразования координат ( пассивные ) в отличие от преобразований точек ( активные ). Поскольку A выражает вращение из локального кадра 1 в глобальный кадр 0 (т. е. A кодирует оси кадра 1 относительно кадра 0 ), элементарные матрицы вращения составляются так, как указано выше. Поскольку обратное вращение — это просто транспонированное вращение, если бы мы хотели глобально-локальное вращение из кадра 0 в кадр 1 , мы бы написали
Матрица вращения ↔ Ось/угол Эйлера
Если угол Эйлера θ не кратен π , ось Эйлера ê и угол θ можно вычислить из элементов матрицы вращения A следующим образом:
В качестве альтернативы можно использовать следующий метод:
Разложение матрицы вращения по собственным значениям дает собственные значения 1 и cos θ ± i sin θ . Ось Эйлера — это собственный вектор, соответствующий собственному значению 1, а θ можно вычислить из оставшихся собственных значений.
Ось Эйлера также можно найти с помощью сингулярного разложения , поскольку это нормализованный вектор, охватывающий нулевое пространство матрицы I − A.
Для преобразования в другую сторону матрицу вращения, соответствующую оси Эйлера ê и углу θ, можно вычислить по формуле вращения Родригеса (с соответствующей модификацией) следующим образом:
где I 3 — единичная матрица 3 × 3 , и
— это матрица перекрестного произведения .
Это расширяется до:
Матрица вращения ↔ кватернион
При вычислении кватерниона из матрицы вращения возникает неоднозначность знака, поскольку q и − q представляют одно и то же вращение.
Один из способов вычисления кватерниона из матрицы вращения A заключается в следующем:
Есть три других математически эквивалентных способа вычисления q . Числовая неточность может быть уменьшена, если избегать ситуаций, в которых знаменатель близок к нулю. Один из трех других методов выглядит следующим образом: [6] [7]
Матрица вращения, соответствующая кватерниону q, может быть вычислена следующим образом: где что дает
или эквивалентно
Это называется формулой Эйлера–Родрига для матрицы преобразования
Углы Эйлера ↔ кватернион
Углы Эйлера (з - х - звнешний) → кватернион
Мы рассмотрим x -соглашение 3-1-3 внешних углов Эйлера для следующего алгоритма. Условия алгоритма зависят от используемого соглашения.
Мы можем вычислить кватернион из углов Эйлера ( ϕ , θ , ψ ) следующим образом:
Углы Эйлера (z - y ′- x ″внутренний) → кватернион
Кватернионный эквивалент углов рыскания ( ψ ), тангажа ( θ ) и крена ( ϕ ) или внутренних углов Тейта-Брайена , следующих соглашению z - y ′- x ″ , может быть вычислен с помощью
Кватернион → Углы Эйлера (з - х - звнешний)
Учитывая кватернион вращения, внешние углы Эйлера 3-1-3 по x -соглашению ( φ , θ , ψ ) можно вычислить следующим образом :
Кватернион → Углы Эйлера (z - y ′- x ″внутренний)
Учитывая кватернион вращения , углы рыскания , тангажа и крена или внутренние углы Тейта-Брайана , следующие соглашению z - y ′- x ″ , можно вычислить следующим образом:
Ось Эйлера–угол ↔ кватернион
Учитывая ось Эйлера ê и угол θ , кватернион
можно вычислить по
Дано кватернион вращения q , определим Тогда ось Эйлера ê и угол θ можно вычислить следующим образом:
Матрица вращения ↔ Вектор Родригеса
Вектор Родригеса → Матрица вращения
Поскольку определение вектора Родригеса можно связать с кватернионами вращения: Используя следующее свойство, формулу можно получить путем разложения q на множители2
риз окончательного выражения, полученного для кватернионов:
Приводим к окончательной формуле:
Формулы преобразования производных
Матрица вращения ↔ угловые скорости
Вектор угловой скорости можно извлечь из производной по времени матрицы вращения д А/д т следующим соотношением:
Вывод адаптирован из Иоффе [8] следующим образом:
Для любого вектора r 0 рассмотрим r ( t ) = A ( t ) r 0 и продифференцируем его:
Производная вектора — это линейная скорость его кончика. Поскольку A — матрица вращения, по определению длина r ( t ) всегда равна длине r 0 , и, следовательно, она не меняется со временем. Таким образом, когда r ( t ) вращается, его кончик движется по окружности, а линейная скорость его кончика направлена по касательной к окружности; т. е. всегда перпендикулярна r ( t ) . В этом конкретном случае соотношение между вектором линейной скорости и вектором угловой скорости следующее (см. круговое движение и векторное произведение ).
В силу транзитивности вышеупомянутых уравнений,
что подразумевает
Кватернион ↔ угловые скорости
Вектор угловой скорости можно получить из производной кватерниона д д/д т следующим образом: [9] где q̃ — сопряженная (обратная) величина q .
Наоборот, производная кватерниона равна
Роторы в геометрической алгебре
Формализм геометрической алгебры (ГА) обеспечивает расширение и интерпретацию метода кватернионов. Центральным в ГА является геометрическое произведение векторов, расширение традиционных внутренних и перекрестных произведений , заданное как
где символ ∧ обозначает внешнее произведение или произведение клина . Это произведение векторов a и b производит два члена: скалярную часть от внутреннего произведения и бивекторную часть от произведения клина. Этот бивектор описывает плоскость, перпендикулярную тому, что вернуло бы перекрестное произведение векторов.
Бивекторы в GA обладают некоторыми необычными свойствами по сравнению с векторами. При геометрическом произведении бивекторы имеют отрицательный квадрат: бивектор x̂ŷ описывает плоскость xy . Его квадрат равен ( x̂ŷ ) 2 = x̂ŷx̂ŷ . Поскольку единичные базисные векторы ортогональны друг другу, геометрическое произведение сводится к антисимметричному внешнему произведению, поэтому x̂ и ŷ можно свободно менять местами за счет коэффициента −1. Квадрат сводится к − x̂x̂ŷŷ = −1, поскольку сами базисные векторы имеют квадрат +1.
Этот результат справедлив в целом для всех бивекторов, и в результате бивектор играет роль, аналогичную мнимой единице . Геометрическая алгебра использует бивекторы в своем аналоге кватерниона, роторе , заданном как где B̂ — единичный бивектор, описывающий плоскость вращения . Поскольку B̂ возводится в квадрат до −1, разложение R в степенной ряд порождает тригонометрические функции . Формула вращения, которая отображает вектор a в повернутый вектор b, имеет вид , где — обратный ( изменение порядка векторов в эквивалентно изменению его знака).
Пример. Вращение вокруг оси можно осуществить, преобразуя v̂ в его дуальный бивектор, где i = x̂ŷẑ — элемент единичного объема, единственный тривектор (псевдоскаляр) в трехмерном пространстве. Результатом будет
Однако в трехмерном пространстве часто проще оставить выражение для B̂ = iv̂ , используя тот факт, что i коммутирует со всеми объектами в 3D, а также квадратируется до −1. Поворот вектора x̂ в этой плоскости на угол θ тогда равен
Признание того, что и что − v̂x̂v̂ является отражением x̂ относительно плоскости, перпендикулярной v̂, дает геометрическую интерпретацию операции вращения: вращение сохраняет компоненты, параллельные v̂ , и изменяет только те, которые перпендикулярны. Затем вычисляются члены:
Результатом вращения тогда будет
Простая проверка этого результата — угол θ = 2/3 π . Такое вращение должно отображать x̂ в ŷ . Действительно, вращение сводится к
точно так, как и ожидалось. Эта формула вращения действительна не только для векторов, но и для любого мультивектора . Кроме того, когда используются углы Эйлера, сложность операции значительно уменьшается. Составные вращения получаются путем умножения роторов, поэтому общий ротор из углов Эйлера равен, но Эти роторы возвращаются из экспонент следующим образом: где R β относится к вращению в исходных координатах. Аналогично для вращения γ , Заметив, что R γ и R α коммутируют (вращения в одной плоскости должны коммутировать), и общий ротор становится
Таким образом, составные вращения углов Эйлера становятся серией эквивалентных вращений в исходной неподвижной системе отсчета.
Хотя роторы в геометрической алгебре работают почти идентично кватернионам в трех измерениях, сила этого формализма заключается в его общности: этот метод уместен и действителен в пространствах с любым числом измерений. В 3D вращения имеют три степени свободы, по одной степени для каждой линейно независимой плоскости (бивектора), в которой может происходить вращение. Известно, что пары кватернионов могут использоваться для генерации вращений в 4D, что дает шесть степеней свободы, и подход геометрической алгебры подтверждает этот результат: в 4D существует шесть линейно независимых бивекторов, которые могут использоваться в качестве генераторов вращений.
Смотрите также
Ссылки
- ^ «Отслеживание координатных маркеров для дополненной реальности».
- ^ Вайсштейн, Эрик В. «Матрица вращения». MathWorld .
- ^ аб Родригес, Олинде (1840). «Des lois géometriques qui regissent les déplacements d'un system Solide dans l'espace, et de lavariation des coordonnées producant de ces déplacement, рассматриваемые как независимые причины, которые могут быть произведены». Дж. Математика. Приложение Pures . 5 : 380–440.онлайн
- ^ см. J Willard Gibbs (1884). Элементы векторного анализа , New Haven, стр. 67
- ^ Конспект лекций по прямой и обратной кинематике, стр. 5
- ^ Мебиус, Йохан (2007). «Вывод формулы Эйлера–Родригеса для трехмерных вращений из общей формулы для четырехмерных вращений». arXiv : math/0701759 .
- ^ Шустер, Малкольм Д. (1993). «Обзор представлений об отношении» (PDF) . Журнал астронавтических наук . 41 (4): 439–517.
- ^ [1] Физика - Марк Иоффе - W ( t ) в терминах матриц
- ^ Конспект лекций по кватернионам и вращению, стр. 14-15
Дальнейшее чтение
- Шустер, МД (1993). «Обзор представлений об отношении» (PDF) . Журнал астронавтических наук . 41 (4): 439–517. Bibcode : 1993JAnSc..41..439S.
- Таубин, Г. (2011). «3D вращения». IEEE Computer Graphics and Applications . 31 (6): 84–89. doi :10.1109/MCG.2011.92. PMID 24808261.
- Кутиас, Э.; Ромеро, Л. (2004). «Кватернионы в приложении к динамике твердого тела». Технический отчет Sandia . Национальные лаборатории Sandia. SAND2004-0153.
- Markley, F. Landis (2003). "Представления ошибок ориентации для фильтрации Калмана". Journal of Guidance, Control and Dynamics . 26 (2): 311–7. Bibcode :2003JGCD...26..311M. doi :10.2514/2.5048. hdl : 2060/20020060647 .
- Голдштейн, Х. (1980). Классическая механика (2-е изд.). Эддисон–Уэсли. ISBN 0-201-02918-9.
- Верц, Джеймс Р. (1980). Определение и управление положением космического корабля . Д. Рейдель . ISBN 90-277-1204-2.
- Шмидт, Дж.; Ниманн, Х. (2001). «Использование кватернионов для параметризации трехмерных вращений в неограниченной нелинейной оптимизации». Труды конференции Vision Modeling and Visualization Conference 2001. С. 399–406. ISBN 3898380289.
- Ландау, Л.; Лифшиц, Э.М. (1976). Механика (3-е изд.). Пергамон Пресс . ISBN 0-08-021022-8.
- Klumpp, AR (декабрь 1976 г.). «Извлечение кватерниона из матрицы направляющих косинусов без сингулярностей». Journal of Spacecraft and Rockets . 13 (12): 754–5. Bibcode : 1976JSpRo..13..754K. doi : 10.2514/3.27947.
- Доран, К.; Ласенби, А. (2003). Геометрическая алгебра для физиков . Cambridge University Press. ISBN 978-0-521-71595-9.
- Терзакис, Г.; Луракис, М.; Айт-Будауд, Д. (2018). «Модифицированные параметры Родригеса: эффективное представление ориентации в трехмерном зрении и графике». Журнал математического изображения и зрения . 60 (3): 422–442. doi : 10.1007/s10851-017-0765-x .
- Ровенхорст, Д.; Роллетт, А.Д.; Рорер, Г.С.; Грёбер, М.; Джексон, М.; Конийненберг, П.Дж.; Де Граеф, М. (2015). "Последовательные представления и преобразования между трехмерными вращениями". Моделирование и имитация в материаловедении и машиностроении . 23 (8): 083501. Bibcode : 2015MSMSE..23h3501R. doi : 10.1088/0965-0393/23/8/083501. S2CID 16130878.
Внешние ссылки
- EuclideanSpace содержит массу информации о представлении вращения.
- Q36. Как сгенерировать матрицу вращения из углов Эйлера? и Q37. Как преобразовать матрицу вращения в углы Эйлера? — Часто задаваемые вопросы о матрицах и кватернионах
- Мнимые числа не являются действительными – Геометрическая алгебра пространства-времени – Раздел «Вращения и геометрическая алгебра» выводит и применяет роторное описание вращений.
- Учебник Starlino's DCM – Учебник по теории направляющих косинусных матриц и приложения. Алгоритм оценки пространственной ориентации с использованием акселерометра, гироскопа и магнитометра IMU. Использование комплементарного фильтра (популярная альтернатива фильтру Калмана) с матрицей DCM.
































![{\displaystyle {\begin{aligned}\mathbf {A} _{X}&={\begin{bmatrix}1&0&0\\0&\cos \phi &-\sin \phi \\0&\sin \phi &\cos \phi \end{bmatrix}}\\[5px]\mathbf {A} _{Y}&={\begin{bmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0& \cos \theta \end{bmatrix}}\\[5px]\mathbf {A} _{Z}&={\begin{bmatrix}\cos \psi &-\sin \psi &0\\\sin \psi & \cos \psi &0\\0&0&1\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d396db64b528dcfaed8795003f033d534ae5de87)



![{\displaystyle \mathbf {A} =\mathbf {I} _{3}\cos \theta +(1-\cos \theta){\hat {\mathbf {e} }}{\hat {\mathbf {e } }}^{\mathsf {T}}+\left[{\hat {\mathbf {e} }}\right]_{\times }\sin \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e2785f256aa4d31f2f9fd0eda8a4290dcc1940)
![{\displaystyle \left[{\hat {\mathbf {e} }}\right]_{\times }= {\begin{bmatrix}0&-e_{3}&e_{2}\\e_{3}&0&- e_{1}\\-e_{2}&e_{1}&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7543a05032b732bedc3c2a829bccdaa4a1767a08)






















![{\displaystyle [{\boldsymbol {\omega }}]_{\times }={\begin{bmatrix}0&-\omega _{z}&\omega _{y}\\\omega _{z}&0&- \omega _{x}\\-\omega _{y}&\omega _{x}&0\end{bmatrix}}={\frac {\mathrm {d} \mathbf {A} }{\mathrm {d } t}}\mathbf {A} ^{\mathsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e77acfcca1f8dcc42a510d9c87e84bc9cac1fee2)

![{\displaystyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\boldsymbol {\omega }}(t)\times \mathbf {r} (t)=[{\boldsymbol {\omega }}]_{\times }\mathbf {r} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ff9424c8647883330a8b9d739cb95a0e06f1c7c)
![{\displaystyle {\frac {\mathrm {d} \mathbf {A} {\mathrm {d} t}}\mathbf {A} ^{\mathsf {T}}(t)\mathbf {r} (t )=[{\boldsymbol {\omega }}]_{\times }\mathbf {r} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74108f541116e51a7ffb72a6f88465b229b727d)
![{\displaystyle {\frac {\mathrm {d} \mathbf {A} {\mathrm {d} t}}\mathbf {A} ^{\mathsf {T}}(t)=[{\boldsymbol {\ омега }}]_{\times }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5501f9dda072f6fd0085a041dc04e2208e7f7a32)





















